КОМБИНАТОРИКА лекция. Комбинаторика
 Скачать 0.72 Mb.
|
|
Лекции 3-4 КОМБИНАТОРИКА Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике. Правила сложения в комбинаторике Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами. Пример 1. В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного? Решение Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек. По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами. Пример 2.Если на первой полке стоит Х-книг, а на второй полке стоит Y книг, то выбрать книгу из первой или второй полки можно X + Y способами. Пример 3. Студент должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практических занятий? Решение X=17, Y= 13. По правилу суммы 17+13 = 30 тем. Правила умножения в комбинаторике 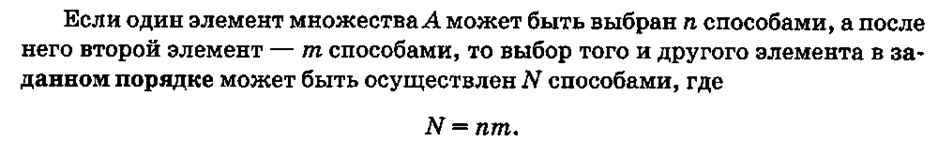 Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:  способами. Пример 4. В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных? Решение Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами. После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами. По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами. Пример 5. . В столовой есть 4 первых блюда и 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать? 4 • 7 = 28 Ответ: 28 вариантов. Пример 6. Сколько различных двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры могут повторяться? 1 цифра – 3 способа 2 цифра – 3 способа 3 • 3 = 9 Ответ: 9 различных двузначных чисел. Факториал     Перестановка Простейшими комбинациями , которые можно составить из элементов конечного множества, являются перестановки. Перестановками называют комбинации, состоящие из одних и тех же n различных объектов и отличающиеся только порядком их расположения. Количество всех возможных перестановок выражается формулой Pn= n! Отличительной особенностью перестановок является то, что в каждой из них участвует ВСЁ множество, то есть, все n объектов. Пример Сколькими способами можно рассадить 5 человек за столом? Решение: используем формулу количества перестановок:  Ответ: 120 способами Пример Четыре студентов пишут ответ на экзаменационный вопрос. Сколькими способами их могут последовательно вызвать отвечать? P4= 4!=1•2•3•4=24 Пример В морозилке лежат шесть порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения? P6= 6!=1•2•3•4•5•6=720 Перестановка с повторением Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы. 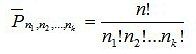 Пример 8. Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»? Решение Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно  Пример 9. Сколькими способами можно собрать гирлянду из 4 красных, 4 синих и 8 желтых флажков? Решение. У нас имеется n1 = 4 объекта первого типа (красные флажки), n2 = 4 объекта второго типа (синие флажки) и n3 = 8 объектов третьего типа (желтые флажки). Все эти n=4+4+8=1 флажков нужно развесить на веревке всеми возможными способами. Применяем формулу числа перестановок с повторениями: P16(4,4,8)=16!4!⋅4!⋅8!=900900. Пример 10. Сколькими способами можно разбить группу 10 друзей на команды из 2 бандитов, 2 полицейских, 1 сыщика и 5 прохожих для игры? Решение. В самой задаче объекты (люди) уже разбиты по типам: n1=2, n2=2, n3=1, n4=5. Осталось лишь применить формулу. Тогда искомое число способов разбиться на персонажи равно: P10(2,2,1,5)=10!2!⋅2!⋅1!⋅5!=7560.P10(2,2,1,5)=10!2!⋅2!⋅1!⋅5!=7560. Сочетания Сочетаниями называют различные комбинации из  объектов, которые выбраны из множества  различных объектов, и которые отличаются друг от друга хотя бы одним объектом. Иными словами, отдельно взятое сочетание – это уникальная выборка из элементов, в которой не важен их порядок (расположение). Общее же количество таких уникальных сочетаний рассчитывается по формуле  .Задача 3 В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? Решение: прежде всего, снова обращаю внимание на то, что по логике условия, детали считаются различными – даже если они на самом деле однотипны и визуально одинаковы (в этом случае их можно, например, пронумеровать). В задаче речь идёт о выборке из 4 деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:  Здесь, конечно же, не нужно ворочать огромные числа  . В похожей ситуации я советую использовать следующий приём: в знаменателе выбираем наибольший факториал (в данном случае  ) и сокращаем на него дробь. Для этого числитель следует представить в виде  . Распишу очень подробно: способами можно взять 4 детали из ящика.Ещё раз: что это значит? Это значит, что из набора 15 различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетания 4 деталей. То есть, каждая такая комбинация из четырёх деталей будет отличаться от других комбинаций хотя бы одной деталью. Ответ: 1365 способами Формуле  необходимо уделить самое пристальное внимание, поскольку она является «хитом» комбинаторики. При этом полезно ПОНИМАТЬ и без всяких вычислений записывать «крайние» значения:  . Применительно к разобранной задаче:– единственным способом можно не выбрать ни одной детали;  способами можно взять 1 деталь (любую из пятнадцати); способами можно взять 14 деталей (при этом какая-то одна из 15 останется в ящике); – единственным способом можно взять все пятнадцать деталей.Пример.Скольким числом способов можно в группе из 30 человек распределить три бесплатные путевки? Решение. Искомое число способов  Сочетание с повторением Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (5) из этих (n*r) предметов? 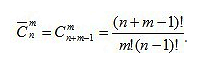 Пример В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных? Решение Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4. 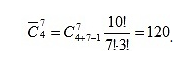 Пример На складе нужно получить 5 однотипных деталей, каждая из которых может быть покрашена в один из трёх цветов: красный, чёрный, зелёный. Сколько имеется способов, чтобы выбрать 5 деталей трёх цветов? Решение 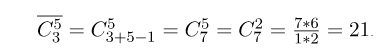  .Ответ Для того, чтобы выбрать 5 деталей 3 цветов, мы нашли 21 способ. Размещения Размещениями называют различные комбинации из 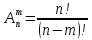объектов, которые выбраны из множества различных объектов, и которые отличаются друг от друга как составом объектов в выборке, так и их порядком. Количество размещений рассчитывается по формуле  Пример В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии? Решение. В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:  Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.  Размещения с повторениями Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом:сколькимиспособамиможновыбратьиразместитьпоm различнымместамm изn предметов,средикоторыхестьодинаковые?  Пример У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик? Решение Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:  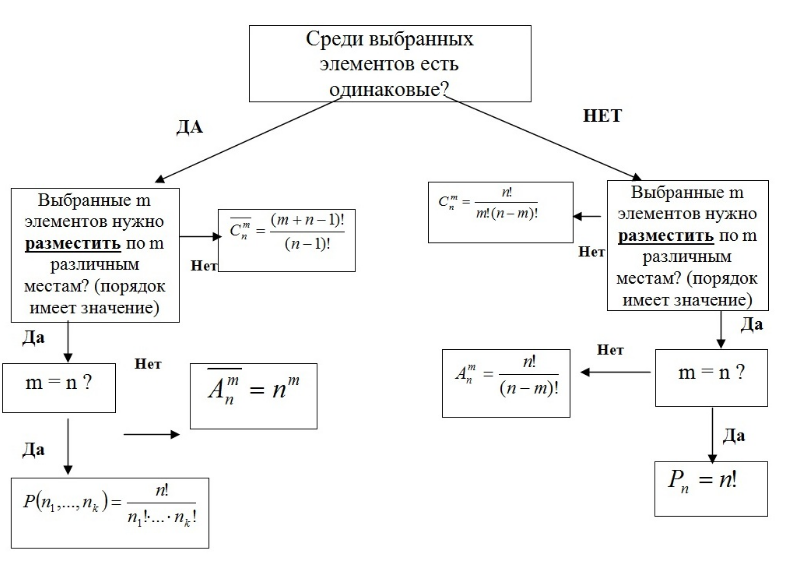.  |