КОМПЬЮТЕРНАЯ МОДЕЛЬ ОБТЕКАНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА ВОЗДУШНЫМИ ПОТОКАМИ И РАСЧЕТ ЕГО АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК. КОМПЬЮТЕРНАЯ МОДЕЛЬ ОБТЕКАНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА ВОЗДУШНЫМИ П. Компьютерная
 Скачать 1.86 Mb. Скачать 1.86 Mb.
|
 Системный анализ УДК 533.6 Ю. В. ЯЦКЕВИЧ, Ю. В. КОЖЕДУБ, Белорусский национальный технический университет,Минский государственный высший авиационный колледж КОМПЬЮТЕРНАЯ МОДЕЛЬ ОБТЕКАНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА ВОЗДУШНЫМИ ПОТОКАМИ И РАСЧЕТ ЕГО АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК В работе описывается оригинальная полуэмпирическая модель турбулентного течения воздуха в погра-ничном слое на поверхности летательного аппарата. На основе этой модели разработана компьютерная си-стема, позволяющая моделировать аэродинамические процессы вокруг летательного аппарата и по результа-там моделирования рассчитывать его аэродинамические характеристики. Эти характеристики используютавиаконструкторы дляоценкикачестваисвойств летательногоаппарата. The original semiempirical model of turbulent flow of air in an interface of an aircraft surface is described in thiswork. Based on this model the computer system allowing to simulate aerodynamic processes around an aircraft and tocalculate it’s aerodynamic characteristics was developed. These characteristics are used by aircraft designers for anassessment ofquality andpropertiesofan aircraft. Современный уровень проектирования ле- тательных аппаратов подразумевает использо- вание тех или иных методов компьютерного моделирования аэродинамической среды, обте- кающей 3d-модель планера при его движении. Поиск приемлемых для практики форм ма- тематического описания турбулентных тече- ний или моделей турбулентности идет уже на протяжении более 100 лет (начиная с класси- ческих работ О. Рейнольдса). Это объясняется исключительной сложностью турбулентности как физического явления. Турбулентные течения, согласно современ- ным представлениям, подчиняются классиче- ским уравнениям Навье-Стокса, и в этом смысле проблема может считаться давно решенной. Од- нако, несмотря на фантастический прогресс вы- числительной техники, наблюдаемый в послед- ние десятилетия, ее возможности все еще недо- статочны для решения этих уравнений при высо- ких разрешениях расчетной сетки (малых шагах дискретизации пространства), представляющих практический интерес. Такая ситуация по самым оптимистичным прогнозам останется вплоть до второй половины, а то и до конца XXI века [1]. В связи с этим, как и ранее, ключевым вопро- сом в рассматриваемой области является поиск приемлемого компромисса между физической адекватностью модели и приемлемым для прак- тического применения уровнем ее сложности. Данная работа посвящена оригинальному программному обеспечению («АэроПро-1»), построенному на основе разработанной авто- рами относительно простой полуэмпирической «подсеточной» модели турбулентного течения на основе уравнения Рейнольдса. То есть, рас- чет распределения скорости (x,y,z,t)по трехмерному пространству моделируемой воз- душной среды производился на основе урав- нения Рейнольдса [2]: x x x x 1 P 2x 2x 2x 'x'y 'x'z t xx yy zz x x2 y2 z2 y z , y y y y 1 P 2y 2y 2y 'y'x 'y'z x y z 2 2 , (1) t x y z y x y z x z z z , z z 1 P 2z 2z 2z 'y'z 'x'z t xx yy zz z x2 y2 z2 y x где t – время; x, y, z – декартовы координаты (ось Y направлена вертикально); x, y, z – проекции скорости воздуха на координатные оси X, Y, Z соответственно; P – давление воз- духа; – плотность воздуха; – динамическая вязкость воздуха; ’x, ’y, ’z – пульсации со- ответствующих проекций скорости воздуха внутри сеточного элемента. Расчет распределения плотности (x, y, z, t) на основании трехмерного поля скоростей (x, y, z, t) производился по уравнению нераз- рывности: ся шаг сетки от 0,05 до 0,2 мм. DNS-модель построена на основе уравнений Навье-Стокса, уравнения неразрывности и уравнения Менде- леева–Клапейрона [4]. Эта модель полностью свободна от эмпиризма (в данной статье не рассматривается). Она позволила выявить ос- новные закономерности возникновения и раз- вития турбулентного слоя в зависимости от шероховатости поверхности, скорости и угла набегающего ламинарного потока по отноше- нию к обтекаемой поверхности (локального угла атаки). Упрощенно предполагается, что погранич- t xx yy zz xyz. (2) ный слой до момента отрыва состоит из дви- жущихся цилиндрических вихревых областей (вихрей), диаметр wкоторых равен толщине x y z слоя . Линейная скорость воздуха прилегаю- Пересчет распределения плотности (x, y, z, t) в поле давлений P(x, y, z, t) производился по уравнению Менделеева-Клапейрона: щего к твердой поверхности равна 0. Воздух на внешнем крае пограничного слоя (внешняя часть вихрей) имеет скорость набегающего ла- минарного потока . Таким образом, центр P M RT, (3) вращения вихря (и сам вихрь) перемещается со скоростью w /2 в направлении воздуш- где Т– температура воздуха; М 0,029 кг/моль – молярная масса воздуха; R 8,3144 Дж/ (мольК) – универсальная газовая постоянная. Данная система уравнений (1–3) является не замкнутой. Для их замыкания нужно опре- делить 6 компонент турбулентных (Рейноль- дсовых) напряжений 'i' j. Для определения Рейнольдсовых напряже- ний используется понятие пограничного слоя. Пограничный слой – тонкий по сравнению с характерным линейным размером тела слой жидкости или газа, прилегающий к твердой поверхности, в котором градиенты газодина- мических переменных в нормальном к стенке направлении столь велики, что инерционные силы и силы трения имеют здесь один и тот же порядок. Течение в этом слое при больших числах Рейнольдса становится турбулентным. Понятие пограничного слоя [3] для анализа движения жидкости при больших числах Рейнольдса было предложено Л. Прандтлем(1904). Разработанная модель основывается на эм- пирических наблюдениях за поведением тур- булентного слоя, смоделированного методом прямого численного моделирования (Direct Number Simulation – DNS) для малого участка поверхности (1×5 см). При этом использовал- ного потока. 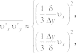 Исходя из этого представления, Рейноль- дсовы напряжения зависят от толщины погра- ничного слоя (диаметра вихрей) и скорости ламинарного потока (усредненной скорости) приблизительно так: Исходя из этого представления, Рейноль- дсовы напряжения зависят от толщины погра- ничного слоя (диаметра вихрей) и скорости ламинарного потока (усредненной скорости) приблизительно так: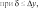 (4) 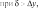 где ’x– пульсация скорости воздуха вдоль об- текаемой поверхности; ’y – пульсация скоро- сти воздуха вдоль нормали к обтекаемой по- верхности; 'x 'y– Рейнольдсово напряже- ние; – толщина пограничного слоя; x– про- екция скорости ламинарного потока на обтека- емую поверхность; y – высота сеточного эле- мента. Как показало DNS-моделирование, турбу- лентный вихрь появляется на поверхности при наличии неровности и еще двух условиях: набегающий поток направлен от поверх- ности, то есть локальный угол атаки внутри сеточного элемента не отрицательный (l 0); скорость набегающего воздушного пото- ка достаточно велика ( 0). 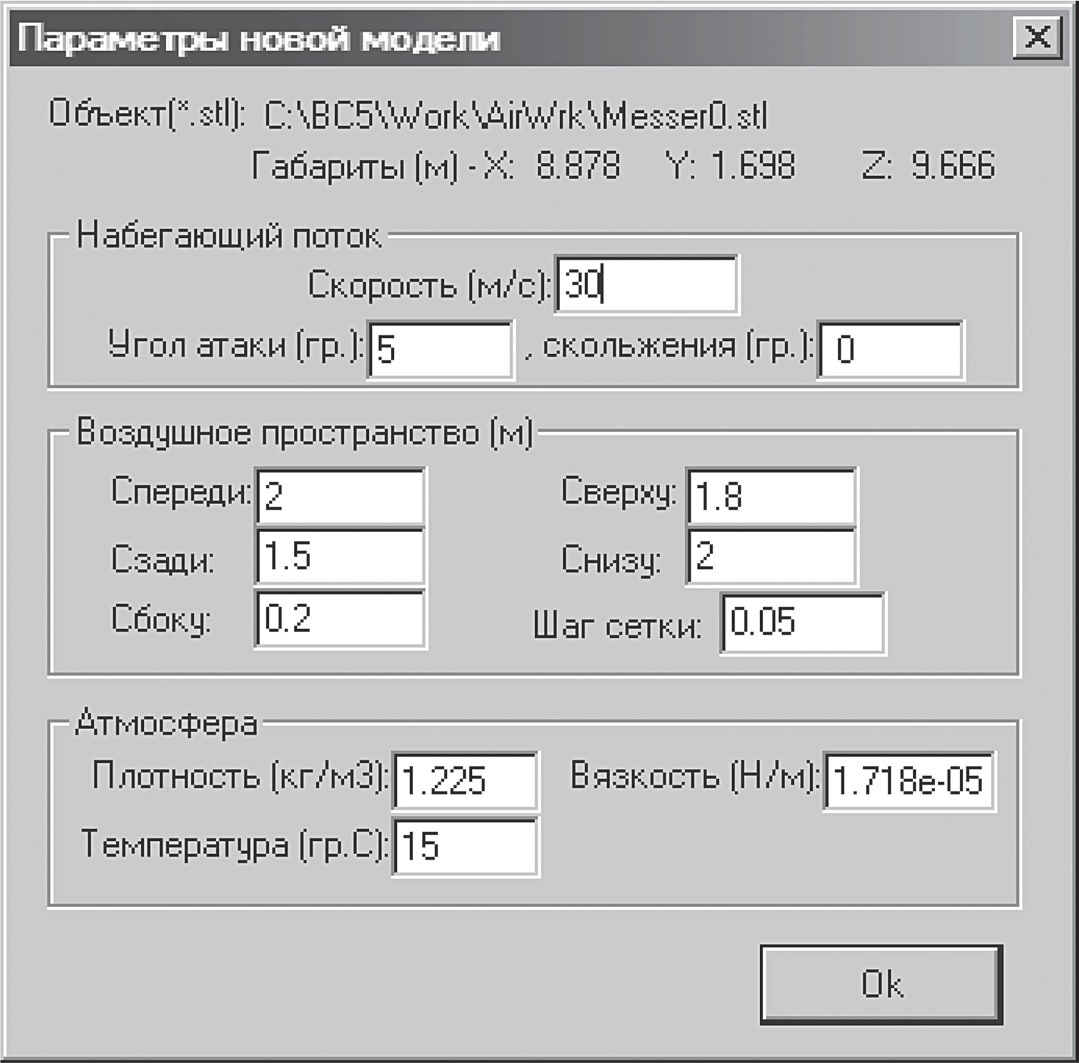 Рис. 1. Панель задания входных параметров при создании новой модели Значение 0 зависит от шероховатости поверхности. В данной работе принимается 0 7 м/с, что соответствует наличию на по- верхности неровностей высотой 0,4 мм. По мере перемещения вихря вдоль набега- ющего потока наблюдается рост его геометри- ческих размеров в результате вовлечения во вращательное движение окружающих масс воздуха. Этот процесс характеризуется скоро- стью роста толщины турбулентного погранич- ного слоя (K /t). По результатам числен- ных экспериментов с различными скоростями набегающего потока была установлена сред- няя величина скорости роста толщины турбу- лентного потока – K 2 м/с. Кроме роста размеров вихрей на геометри- ческую конфигурацию турбулентного слоя оказывает влияние усредненная скорость тече- ния воздуха. В целом изменение толщины тур- булентного слоя в разработанной модели опи- сывается уравнением: вания турбулентного слоя (l 0 и 0), то есть в компьютерной модели анализируется угол наклона набегающего потока к обтекае- мой поверхности в каждом граничном конеч- но-разностном элементе. Эта математическая модель была положена в основу компьютерной модели, в которой мо- делируемое пространство разбивается на пря- моугольные элементы (прямоугольную сетку). Элементы, пересекающие поверхность твер- дого объекта, имеют трапециевидную форму (конечно-объемное представление на границах твердого объекта). Кроме описания геометрии объекта в фор- мате «*.stl» входными данными для моделиро- вания являются: скорость набегающего пото- ка, угол атаки (угол между направлением воз- душного потока и продольной осью самолета в вертикальной плоскости), угол скольжения (угол между направлением воздушного потока и продольной осью самолета в горизонтальной плоскости), размеры воздушного пространства K . (5) с разных сторон относительно летательного t xx yy zz аппарата, а также – характеристики атмосфе- ры (рис. 1). Таким образом, уравнения (1–5) представ- ляют собой замкнутую систему, описываю- щую динамику воздушных потоков в про- странстве вокруг летательного аппарата. В нее также необходимо включить условия образо- На рис. 2, 3 представлены результаты мо- делирования в виде полей скоростей и давле- ний воздуха по сечениям моделируемого про- странства, а также в проекциях на поверхность самолета. 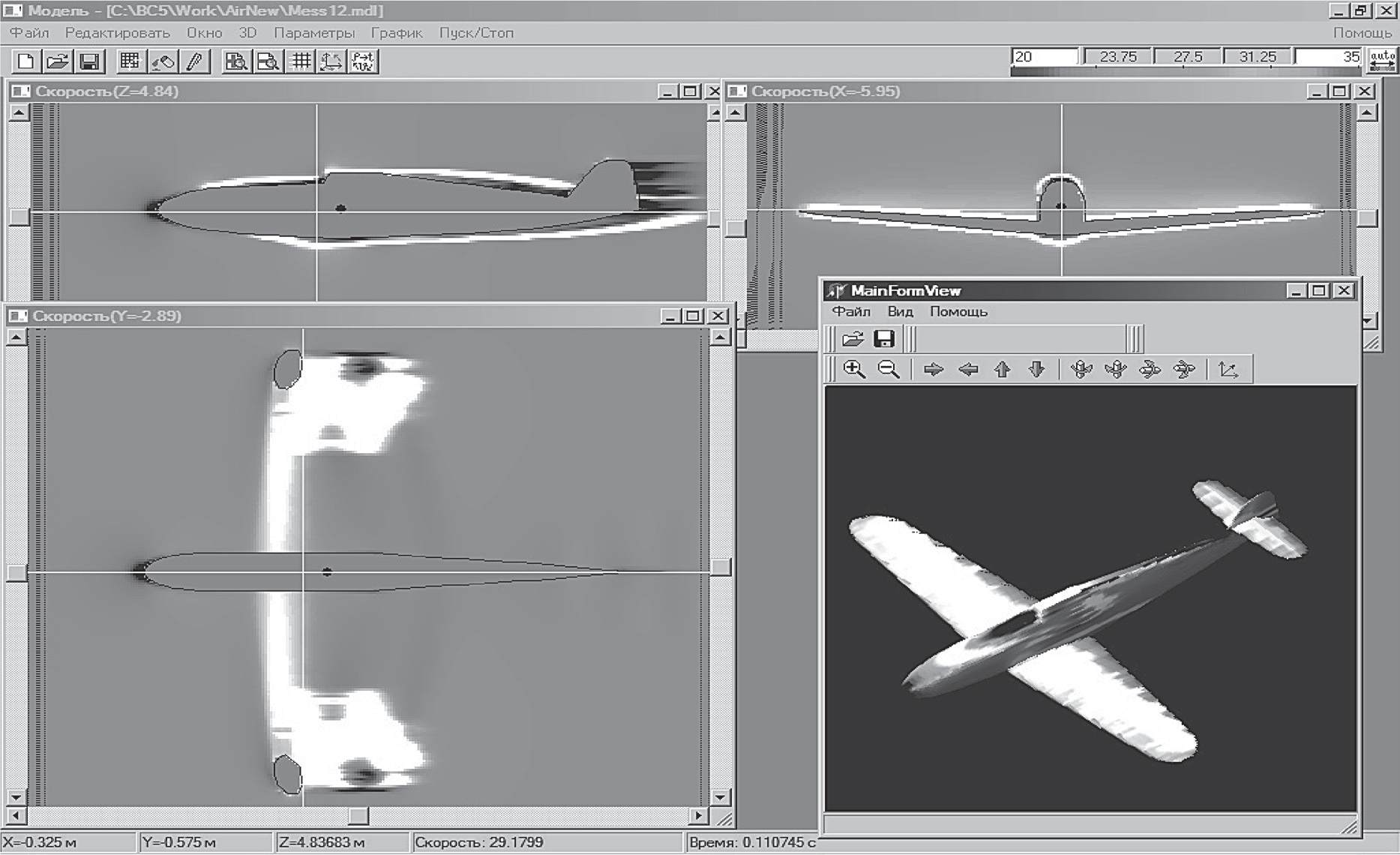 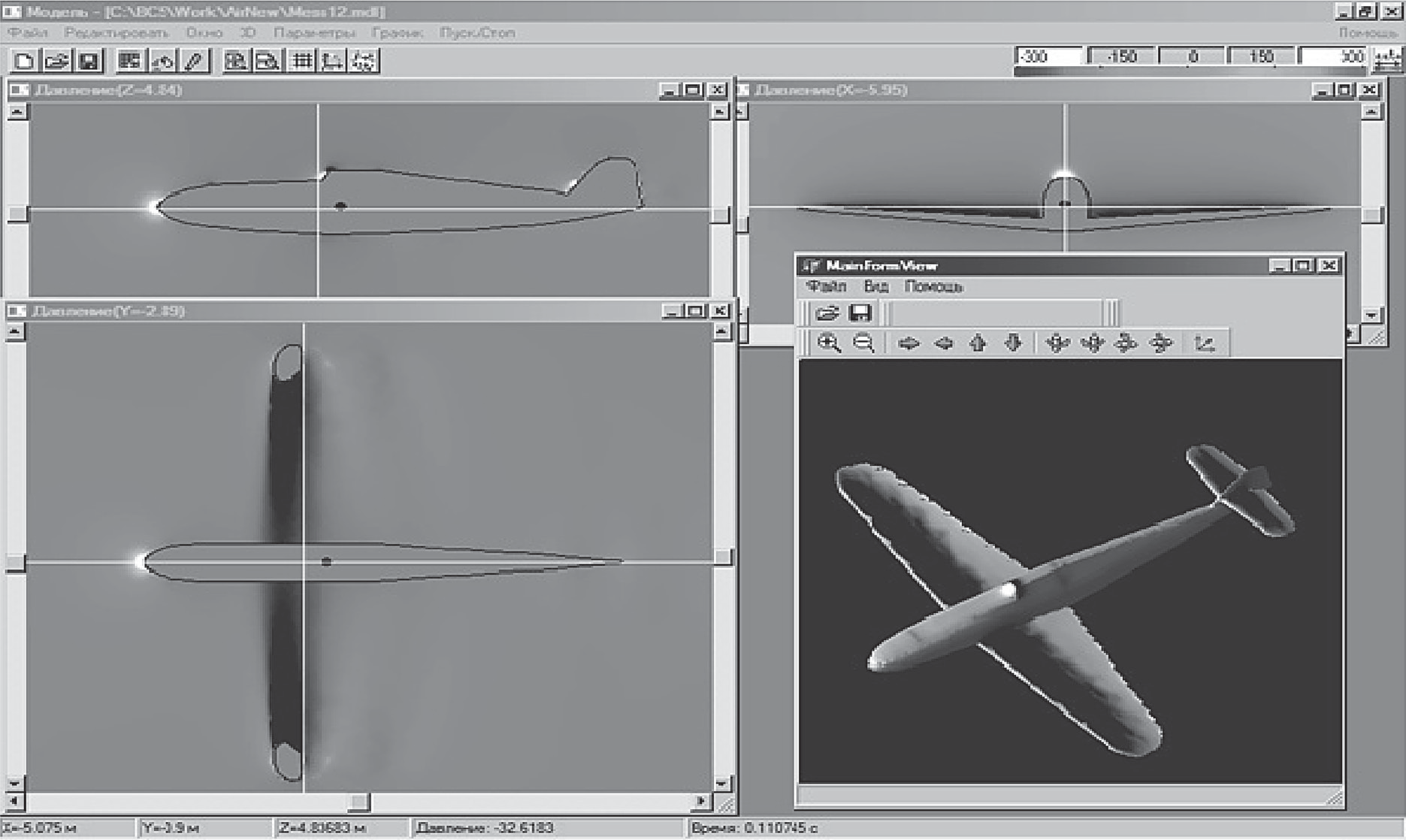 Рис. 2. Интерфейс программы при отображении распределения скоростей воздуха по сечениям моделируемого пространства и по поверхности самолета при угле атаки набегающего потока 0º Рис. 2. Интерфейс программы при отображении распределения скоростей воздуха по сечениям моделируемого пространства и по поверхности самолета при угле атаки набегающего потока 0ºРис. 3. Интерфейс программы при отображении распределения давлений воздуха по сечениям моделируемого про- странства и по поверхности самолета при угле атаки набегающего потока 0º На основе полученных трехмерных полей давлений рассчитываются основные аэродина- мические характеристики самолета [5] (лобо- вое сопротивление и подъемная сила, момен- ты тангажа, рыскания и крена). Аэродинамические характеристики вы- числялись следующим образом. Вначале вы- числялись силы давления, действующие с раз- ных сторон на самолет, путем суммирования сил давления каждого конечно-объемного элемента, пересекающего поверхность объ- екта: 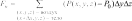 , (6) , (6) , (7) , (7) , (8) , (8)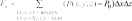 , (9) , (9)где Fп – сила давления, действующая на объ- ект спереди, Fз – сзади, Fв – сверху, Fн – снизу, P(x, y, z) – давление в конечно-разностном эле- менте с координатами (x, y, z); P0 105005 Па – нормальное давление воздуха; x, y, z– шаг конечно-разностной сетки. Затем, на основании полученных сил, дей- ствующих с разных сторон на объект, вычис- лялись лобовое сопротивление: 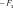 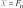 , (10) , (10)В разработанной программе вращающие моменты вычисляются относительно осей вра- щения, проходящих через центр тяжести само- лета, координаты которого (хс, yс, zс) задаются в программе перед началом моделирования. В процессе расчета просматриваются все пары соседних конечноразностных элементов, в ко- торых один элемент принадлежит твердому телу (летательному аппарату), а второй – воз- душному пространству. Произведение давле- ния в пограничном воздушном элементе на его расстояние до центра тяжести и площадь гра- ни дает вращающий момент. А сумма всех эле- ментарных вращающих моментов дает пол- ный вращающий момент летательного аппа- рата: 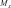 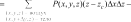   (14) (14)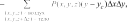 подъемная сила: подъемная сила: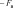 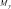 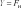 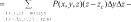 , (11) , (11)коэффициент лобового сопротивления:  коэффициент подъемной силы: где Sн – площадь несущей поверхности (верти- кальной проекции самолета), 0 – нормальная плотность воздуха (на бесконечном удалении от самолета); – скорость воздуха на беско- нечном удалении от самолета. Для вычисления вращающих моментов нужно более подробное описание системы ко- ординат: ось Х направлена вдоль оси самолета от носовой части к хвостовому оперению, ось Y направлена вертикально (перпендикулярно плоскости крыльев), ось Z направлена вдоль крыльев. Тогда крен соответствует вращению самолета вокруг оси X, рыскание – вращение самолета вокруг оси Y, тангаж – вращение са- молета вокруг оси Z. (15) 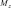 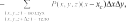 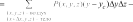  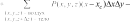 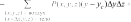 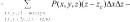 (16) (16) где Mx,My,Mz– моменты крена, рыскания и тан- гажа соответственно; P(x, y, z) – давление воз- духа в конечно-разностном элементе с коорди- 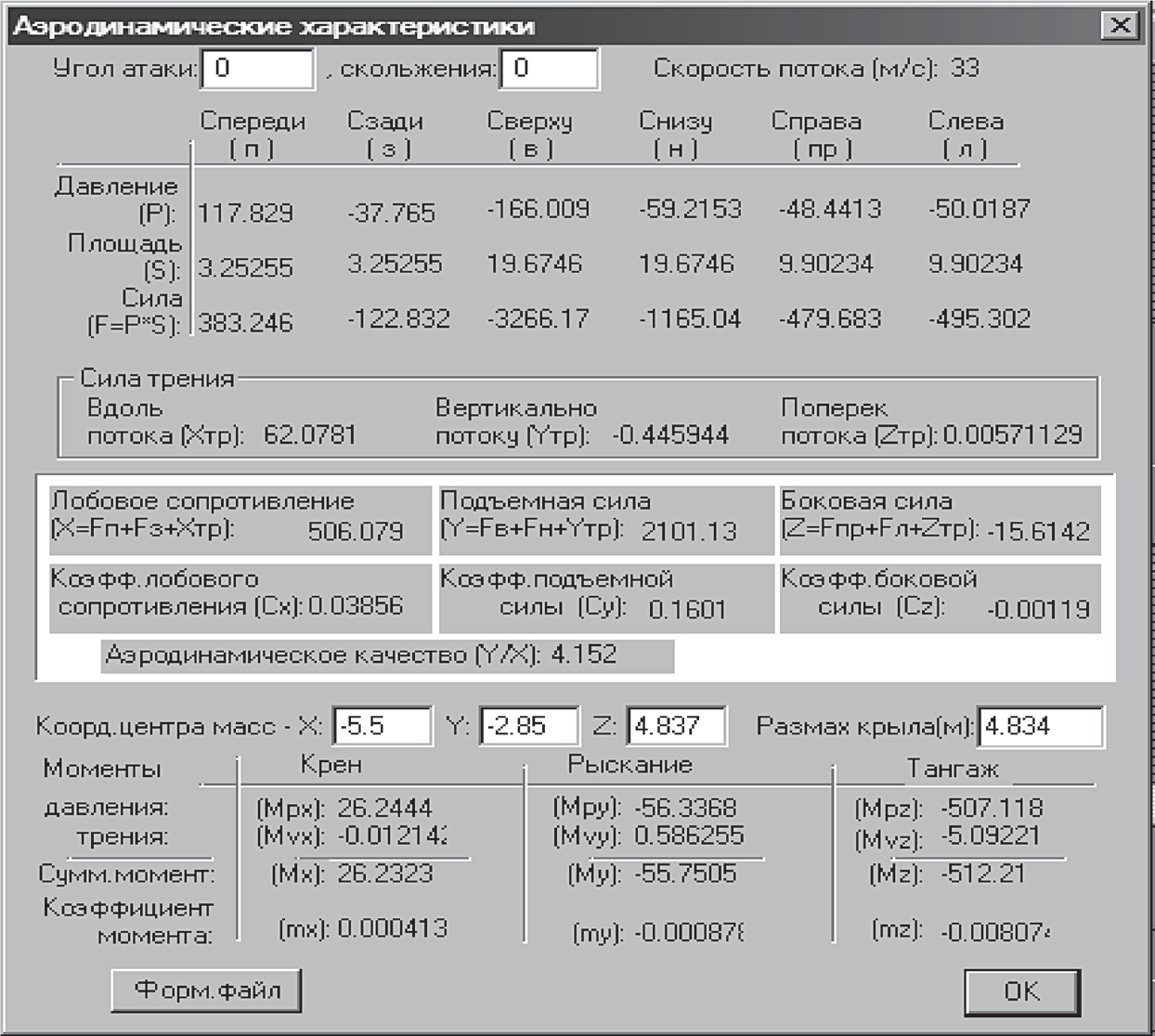 Рис. 4. Панель результатов расчета аэродинамических характеристик программой «АэроПро-1» натами (x, y, z); x, y, z – шаг конечно-раз- ностной сетки. На основании полученных моментов вы- числялись соответствующие коэффициенты: где mx, my, mz – аэродинамические коэффици- енты моментов крена, рыскания и тангажа со- ответственно; Sн – площадь несущей поверх- ности (вертикальной проекции самолета), 0 – нормальная плотность воздуха (на бесконеч- ном удалении от самолета); – скорость воз- духа на бесконечном удалении от самолета; l– размах крыльев. Пример результатов расчетов аэродинами- ческих характеристик самолета программой «АэроПро-1» представлен на рис. 4. Точность расчетов программы оценивалась путем моделирования и сравнения основных аэродинамических характеристик крыльев типо- вых профилей (лобовое сопротивление и подъ- емная сила) с известными данными [6] по ре- зультатам продувки этих крыльев в аэродина- мических трубах. Это сравнение показало, что разработанная компьютерная модель количе- ственно и качественно хорошо имитирует ре- альное поведение крыльев на углах атаки до 12º. Погрешность определения лобового сопро- тивления не превышает 13%, а погрешность определения подъемной силы не превышает 5%. Однако, на больших углах атаки (>12º), соот- ветствующих срыву воздушного потока с обте- каемой поверхности, наблюдается значительное несоответствие с натурными экспериментами.  Литература ЛитератураГарбарук А. В. Моделирование турбулентности в расчетах сложных течений: учебное пособие / А. В. Гарбарук, М. Х. Стрелец, М. Л. Шур – СПб: Изд-во Политехн. ун-та, 2012. – 88 с. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен/ В 2х т., т. 2: [Пер. с англ.]. – М.: Мир., 1990. Шлихтинг Г. Теория пограничного слоя, пер. с нем., М.: Наука, 1974. – 711 с. Белов И. А., Исаев С. А. Моделирование турбулентных течений: Учебное пособие / Балт. гос. техн. ун-т. СПб., 2001. 108 с. Микеладзе В. Г., Титов В. М. Основные геометрические и аэродинамические характеристики самолетов и ракет: Справочник. – М.: Машиностроение, 1982. – 149 с.  1, 2015 СИСТЕМНЫЙ АНАЛИЗ И ПРИКЛАДНАЯ ИНФОРМАТИКА   |
