Вопрос №15
V2
|
Берілген матрицалар А = 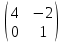 және В = және В = 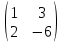 матрицасы. АВ және ВА матрицаларының көбейтіндісін табыңыз матрицасы. АВ және ВА матрицаларының көбейтіндісін табыңыз
(Даны матрицы А = 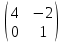 и матрица В = и матрица В = 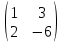 . Найдите произведение матриц АВ и ВА . Найдите произведение матриц АВ и ВА
|
0
|
АВ = ВА = 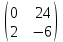
|
0
|
АВ = 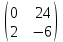
|
0
|
АВ = 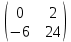
|
0
|
ВА = 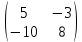
|
0
|
ВА = 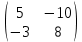
|
0
|
АВ = 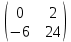
|
Вопрос №16
V2
|
Матрицаның рангісі деп ... аталады.
(Ранг матрицы -
|
0
|
сызықтық тәуелді жолдардың максималды саны
(– это максимальное количество линейно зависимых строк
|
0
|
сызықтық тәуелсіз жолдардың максималды саны
(– это максимальное количество линейно независимых строк
|
0
|
сызықтық тәуелді бағандардың максималды саны
(– это максимальное количество линейно зависимых столбцов
|
0
|
сызықтық тәуелді жолдар мен сызықтық тәуелсіз бағандардың максималды саны
(– это максимальное количество линейно зависимых строк и линейно независимых столбцов
|
0
|
сызықтық тәуелсіз бағандардың максималды саны
(– это максимальное количество линейно независимых столбцов
|
0
|
сызықтық тәуелсіз жолдар мен сызықтық тәуелді бағандардың максималды саны
(– это максимальное количество линейно независимых строк и линейно зависимых столбцов
|
Вопрос №17
V2
|
Рангісі 2-ге тең болатын матрицаны көрсетіңіз
(Укажите матрицу, ранг которой равен 2
|
0
|
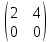
|
0
|
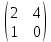
|
0
|
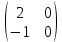
|
0
|

|
0
|

|
0
|
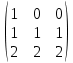
|
Вопрос №18
V2
|
Найти 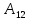 матрицы матрицы 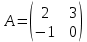 матрицасының матрицасының 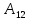 табыңыз табыңыз
|
0
|
1
|
0
|
-1
|
0
|
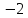
|
0
|
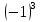
|
0
|
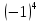
|
Вопрос №19
V2
|
Найти 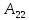 матрицы матрицы 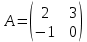 матрицасының матрицасының 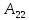 табыңыз табыңыз
|
0
|
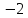
|
0
|
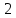
|
0
|
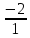
|
0
|
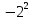
|
0
|
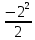
|
Вопрос №20
V2
|
Найдите обратную матрицу к матрице А = 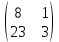 матрицасына кері матрицаны табыңыз матрицасына кері матрицаны табыңыз
|
0
|
А-1 = 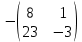
|
0
|
А-1 = 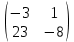
|
0
|
А-1 = 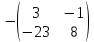
|
0
|
А-1 = 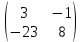
|
0
|
А-1 = 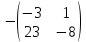
|
Вопрос №21
Вопрос №22
V2
|
Арас көбейтіндінің қасиетін көрсет
(Выберите свойства смешанного произведения векторов
|
0
|
Арас көбейтінді нөлге тең, егер векторлар перпендикуляр болғанында
(Смешанное произведение трех векторов равно нулю тогда и только тогда,
когда эти векторы перпендикулярны.
|
0
|
Арас көбейтінді нөлге тең, егер векторлар компланар болғанында
(Смешанное произведение трех векторов равно нулю тогда и только тогда,
когда эти векторы компланарны.
|
0
|
Егер векторлар компланар емес болса, онда аралас көбейтіндісінің модулі осы векторлардан құралған ұшбұрыштың көлеміне тең
(Если векторы 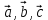 − некомпланарны, то модуль смешанного произведения − некомпланарны, то модуль смешанного произведения
равен объему треугольника, построенного на этих векторах.
|
0
|
Егер векторлар компланар емес болса, онда аралас көбейтіндісінің модулі осы векторлардан құралған параллелепипедтің көлеміне тең
(Если векторы 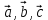 − некомпланарные, то модуль смешанного произведения − некомпланарные, то модуль смешанного произведения
равен объему параллелепипеда, построенного на этих векторах.
|
0
|
Бәрі дұрыс (Все ответы правильны
|
Вопрос №23
V2
|
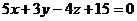 және және 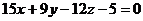 , , 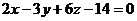 және және 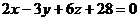 жазықтықтарының қашықтығын табыңдар(параллель жазықтықтар). жазықтықтарының қашықтығын табыңдар(параллель жазықтықтар).
(Укажите расстояние между параллельными плоскостями)
|
0
|
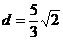 ; ;
|
0
|
;
|
0
|
.
|
0
|
;
|
0
|
;
|
Вопрос №24
V2
|
Кенiстiктегi декарт координат жүйесiндегi 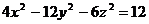 , , 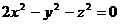 теңдеулер қандай беттердi анықтайды? теңдеулер қандай беттердi анықтайды?
(Какие поверхности описывают уравнения?)
|
0
|
эллипстік цилиндр;(эллиптический цилиндр)
|
0
|
гиперболалық параболоид;(гиперболичесий параболоид)
|
0
|
екі қуысты гиперболоид; (двуполостной гиперболоид)
|
0
|
параболалық цилиндр. (параболический цилиндр)
|
0
|
конус;
|
Вопрос №25
V2
|
Кенiстiктегi декарт координат жүйесiндегi 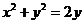 , теңдеулер қандай беттердi анықтайды? , теңдеулер қандай беттердi анықтайды?
(Какие поверхности описывают уравнения?)
|
0
|
шеңбер; (окружность)
|
0
|
конус.
|
0
|
дөңгелек цилиндр;
|
0
|
гиперболалық цилиндр; (гиперболический цилиндр)
|
0
|
параболалық цилиндр; (параболический цилиндр)
|
Вопрос №26
V2
|
Кенiстiктегi декарт координат жүйесiндегi , теңдеулер қандай беттердi анықтайды?
(Какие поверхности описывают уравнения?)
|
0
|
параболалық цилиндр;(параболический цилиндр)
|
0
|
конус.
|
0
|
шеңбер; (окружность)
|
0
|
дөңгелек цилиндр; (круговой цилиндр)
|
0
|
гиперболалық цилиндр; (гиперболический цилиндр)
|
Вопрос №27
V2
|
Кенiстiктегi декарт координат жүйесiндегi , теңдеулер қандай беттердi анықтайды?
(Какие поверхности описывают уравнения?)
|
0
|
шеңбер; (окружность)
|
0
|
конус.
|
0
|
дөңгелек цилиндр;(круговой цилиндр)
|
0
|
эллипстік цилиндр; (эллиптический цилиндр)
|
0
|
параболалық цилиндр; (параболический цилиндр)
|
Вопрос №28
V2
|
Екінші ретті сызықтың теңдеуін канон түріне келтіріп түрін ата.
(Уравнение кривой второго порядка приведите к каноническому виду и назовите ее 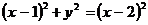
|
0
|
эллипс
|
0
|
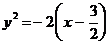
|
0
|
парабола
|
0
|
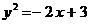
|
0
|
гипербола
| |
 Скачать 1.16 Mb.
Скачать 1.16 Mb.