сущность дифференцированного подхода к организации учебного сотр. Конкурса Учитель года России 2017 Дифференцированный подход в обучении математике
 Скачать 262.84 Kb. Скачать 262.84 Kb.
|
Тема «Законы арифметических действий»
Тема «Формулы». 5 класс
Тема «Уравнения». 5 класс
Приложение 3 Карточки – консультанты Тема «Сложение положительных и отрицательных чисел». 6 класс
Тема «Сложение и вычитание десятичных дробей». 5 класс
Приложение 4. Тема «Положительные и отрицательные числа». 6 класс
Приложение 5 Тема «Делимость чисел» II, III ступени 8*100=235,4 8*6-27= :100=2,354 *6-10=44 *0,1=23,54 (20+)*8=720 :0,1=23,54 (-200):=90. *1000=53,7 2. Добавить в середине две цифры так, чтобы число 356 делилось без остатка на 9. 3. Запиши пары значений и , при которых значение выражения 12*+45*. Делится на 2 Не делится на 5 Делится на 2 и на 5 Не делится ни на 2, ни на 5 4. Наташа забыла первую цифру в коде замка: 85327, но помнила, что всё шестизначное число было кратно 3. Сколько вариантов кода в самом худшем случае надо набрать Наташе, чтобы попасть к себе домой? Приложение 6 Задания с выбором ответа Тема «Десятичные дроби». 5 класс I ступень 1.Выполните деление: 17,1: 9 а)1,9 б) 19 в) 0,19 г)1,99 2.Найдите сторону квадрата с периметром 36,8см. а)92 см б)9,2 см в)18,4 см 3.Чтобы разделить десятичную дробь на натуральное число, надо: а) 1) разделить дробь на это число, не обращая внимания на запятую; 2) поставить в частном запятую, когда кончится деление целой части. Б) 1) умножить ее на это число, не обращая внимания на запятую; 2) в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби. II ступень 1.Найдите значения выражения: 2,4: 4 + 15,3: 5 + 16,4: 8 + 0,15: 3 а)4,6775 б)0,0625 в)0,0005 г)5,76 2. Собрали 36,9 т клубники. На консервный завод отправили 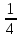 т собранной клубники, а остальную клубнику передали для продажи населению. Сколько тонн клубники было продано населению? т собранной клубники, а остальную клубнику передали для продажи населению. Сколько тонн клубники было продано населению?а)9,225 т б) 23,56 т в)9,3т г) 13,3т 3.Решите задачу: В двух корзинах 16,8 кг помидоров. В одной корзине в 2 раза больше помидоров, чем в другой. Сколько килограммов помидоров в каждой корзине? а)5,6 и 11,2 б) 4,4 и 12,6 в)8,4 и 8,4 г) 6,2 и 10, 6 IIIступень 1.Вычислите: 1,24: 3,1 + 12: 0,25 – 2:25 + 18: 0,45 а)88,32 б)48 в)88,012 г)88,48 2. Если задуманное число умножить на 2,4 и из полученного результата вычесть задуманное число, то получится 7. Найдите задуманное число. а)6,8 б)3,1 в)4 г)5 3. Для упаковки тортов приготовили коробки. Основание каждой коробки – квадрат с длиной стороны 25,5 см. Высота коробки 15,4 см. вычислите объем коробки. Результат округлите до целых. Приложение 7 Задания с выбором ответа Тема «Решение квадратных неравенств». 9 класс I ступень 1. Найдите на рисунке 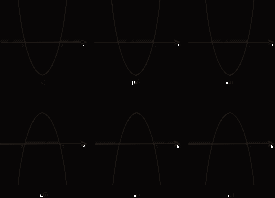 графическую интерпретацию решения каждого из данных неравенств. а)– 2 х² + 10х – 12 > 0; б)– 0,2 х² + х – 1,2 ≤ 0; в)х² - 5х + 6 < 0; г) 3х² - 15х + 18≥ 0.5. 2. Укажите решение неравенства х² - 3х – 4 ≥ 0. а)-1 < х < 4; б) х < -1, х > 4; в)-1 ≤ х ≤ 4; г)х ≤ -1, х ≥ 4. II ступень 1. Укажите решение неравенства - х² + 3х + 10 > 0. а)- 2 < х <5; б)х < - 2, х > 5; в)-2 < x < 5; г) x ≤ -2, x ≥5. 2. Найдите на рисунке 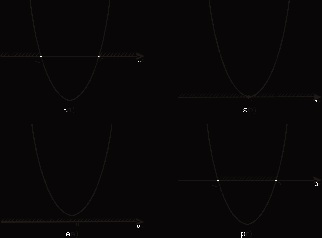 графическую интерпретацию решения неравенства х² + 2х < 0. 3. Найдите на рисунке  графическую интерпретацию решения неравенства 2х < х². 4. Найдите на рисунке 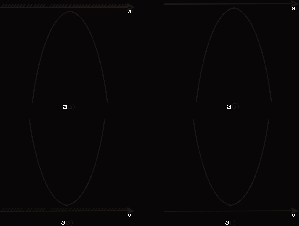 графическую интерпретацию решения неравенства 4х² - 5х + 9 > 0. 5. Укажите решение неравенства -4х² + 5х – 9 ≤ 0. а) нет решений; б)х ≤ -1, х ≥ 2; в)R; г)-1 ≤ х ≤ 2. III ступень 1. Найдите на рисунке 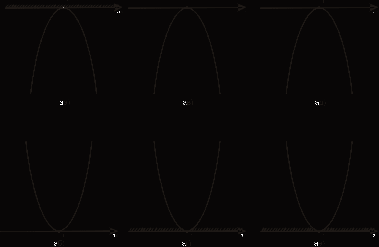 графическую интерпретацию решения каждого из данных неравенств. а) х² + 2х + 1 > 0; б) - х² - 2х -1 < 0; в) х² + 2х + 1 ≤ 0; г) -х² - 2х – 1 ≥ 0. 2. Укажите решение неравенства х² - 6х + 9 > 0 а) нет решений; б)х < 3, х > 3; в)R; г)3 3. Укажите решение неравенства - х² + 6х – 9 ≥ 0. а)R; б)3; в) нет решений; г) х < 3, х> 3. Приложение 8 Тест (время выполнения 15 минут) 6 класс. Тема: Координатная прямая. Модуль числа. Сравнение положительных и отрицательных чисел. 1.Координата точки А на координатной прямой   5 0 X 1)– 0,2; 2) 0,2; 3) – 2; 4) -52. 2.Из чисел – 65 и 75выберите то, у которого модуль больше 1)– 65; 2) – 75; 3) 65; 4) 75. 3. Какой знак надо поставить вместо *, чтобы получилось верное соотношение - 15,3 * 15,3 1) 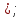 2) 2)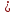 ; 3) =; 4) такого знака нет. ; 3) =; 4) такого знака нет. 4. Какие цифры надо написать вместо *, чтобы получилось верное неравенство - 5761 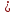 - 576* - 576* 1) 0; 2) 2,3,4,5,6,7,8,9; 3) 1; 4) только 2. 5. Чему равно - (-а) 1) –а; 2) 0; 3) а; 4) любое число. 6. Найди среди чисел противоположные числа: 31; - 3; - 1,3; - 43; 0,75; 34; 0; 3 1) – 43и 34; 2) 3 и – 3; 3) – 43 и 0,75; 4) – 3 и – 1,3 7 А . Найдите координату точки А  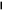 4 -4 1; 2) 0; 3) 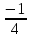 ; 4) ; 4) 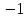 8. Какие целые числа расположены на координатной прямой между числами – 5 и 2 1) -5; -4; -3; -2; -1; 0; 1; 2 2) 0; 1 3) -4; -3; -2; -1; 0; 1 4) -4; -3; -2; -1; 0 Критерий оценивания: 1-4 верно выполненных заданий – оценка «2», 5 верно выполненных заданий – оценка «3», 6-7 верно выполненных заданий – оценка «4», 8 верно выполненных заданий – оценка «5». Приложение 9 Тема «Положительные и отрицательные числа». 5 класс Карточки для работы над теоретическим материалом и заданиями 1 уровня. 1.Выберите необходимые условия для того, чтобы прямая была координатной (подчеркните): Прямая должна быть разделена черточками; указано направление; определен единичный отрезок; нанесены точки; указано начало отсчета 2. Вставьте пропущенное слово в предложения: а) Число, показывающее положение точки на прямой, называют___________этой точки. б) Числа со знаком «+» называют __________. в) Числа со знаком « - « называют ______________. г) Два числа, отличающиеся друг от друга только знаками, называют __________________. 3. Из чисел 23; –6,12; 0; 476; – 76; -1; 0,35 выпишите: а) положительные числа; б) отрицательные числа; в) число, которое не относится ни к положительным, ни к отрицательным; г) противоположные числа. 4. Запишите, как называется расстояние от начала координат до данной точки____________. 5. Может ли модуль какого-нибудь числа быть отрицательным? ______ 6. Найдите: |9|; |–18|; |0|; |–11,5|. 7. Какой число больше: положительное или отрицательное? (подчеркните ответ). 8. Вставьте пропущенное слово: из двух отрицательных чисел больше то, у которого модуль___________. 9. Какими числами выражается увеличение любой величины? _______________. Какими числами выражается уменьшение любой величины? _______________. 10. Поставьте знак <, > или = между числами: а) 0 __34; б) –25__0; в) –7,4__7,2; г) –15__–20. Приложение 10 Контрольная работа. Тема «Положительные и отрицательные числа». 6 класс I уровень 1. Запишите числа, противоположные данным числам: 42; +8,1; -7; -27,5 2.Сравните числа: а) -54 и -13; в)1/2 и -1/2 б)-16,1 и -17,1; г) -250 и 0. 3.Вычислите: а) -60 + 30; в) – 4,2 + (-5,8); б) 25 – 35; г) -5/8 – 2/8. 4. Запишите все целые числа, расположенные на координатной прямой между числами -6 и 6. II уровень Вычислите: 37 – (- 45 + 31) + (-57 – 49) -100. 2.Запишите числа в порядке возрастания: -16; 4/7; -27; 0; -5/6. 3.Вычислите сумму и разность чисел: а) -50,8 и 27,9; б) – 3,27 и -14,003. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 2 = 22 км
2 = 22 км