Конспект лекций по надежности. Конспект лекций по надежности (2). Конспект лекций для студентов специальности 030600 Технология и предпринимательство

• Название: Конспект лекций для студентов специальности 030600 Технология и предпринимательство
• Анкор: Конспект лекций по надежности
• Дата: 25.11.2021
• Размер: 1.18 Mb.
• Имя файла: Конспект лекций по надежности (2).doc
• Тип: Конспект лекций; #282026
• страница: 5 из 6

Вопросы для самоконтроля

1. 
   Каким образом в повышении надежности используется принцип избыточности?
   
2. 
   Как соотносятся конструктивное соединение элементов системы и структурные схемы надежности?
   
3. 
   В чем суть и цель резервирования элементов?
   
4. 
   Если в двигателе внутреннего сгорания предусмотрено 4 цилиндра, можно ли утверждать об использовании в этом случае резервирования?
   
5. 
   Чем отличается резервирование замещением от резервирования дублированием с восстановлением?
   
6. 
   Что эффективнее: общее резервирование системы или раздельное? Какое из них сложнее в реализации?
   
7. 
   В чем особенность записи при составлении аналитических логических моделей надежности систем с резервированием?
   

«Представляется, что для нашей эпохи характерны совершенство средств и путаница целей»

Альберт Эйнштейн

Лекция 10. Методы расчета соединений деталей на надежность

10.1. Расчет надежности резьбовых соединений 10.2. Расчет надежности сварных соединений 10.3. Расчет надежности соединений с натягом

Нераскрытие стыка, несдвигаемость стыка, статическая прочность, сопротивление усталости, затяжка резьбы, предел выносливости, коэффициент трения, концентрация напряжений, ручная, автоматическая сварка, стыковая сварка, сварка внахлестку, в тавр, эквивалентное напряжение, соединение с натягом, модуль упругости, коэффициент поперечного сжатия

10.1. Расчет надежности резьбовых соединений
Вероятность безотказной работы резьбового соединения рассчитывается как произведение вероятностей безотказной работы по четырем основным критериям:

P_рез=P₁·P₂·P₃·P₄,

где P₁ – вероятность безотказнойработы по нераскрытию стыка;

P₂ – вероятность безотказной работы по несдвигаемости деталей стыка;

P₃ – вероятность безотказной работы по статической прочности;

P₄ – вероятность безотказной работы по сопротивлению усталости.

Полагаем, что распределение вероятностей безотказной работы соединения по всем критериям подчиняется закону нормального распределения. Тогда P₁, P₂, P₃, P₄ определяются в зависимости от значения соответствующей квантили u_p1, u_p2, u_p3, u_p4 с учетом соответствующих коэффициентов запаса n₁, n₂, n₃, n₄.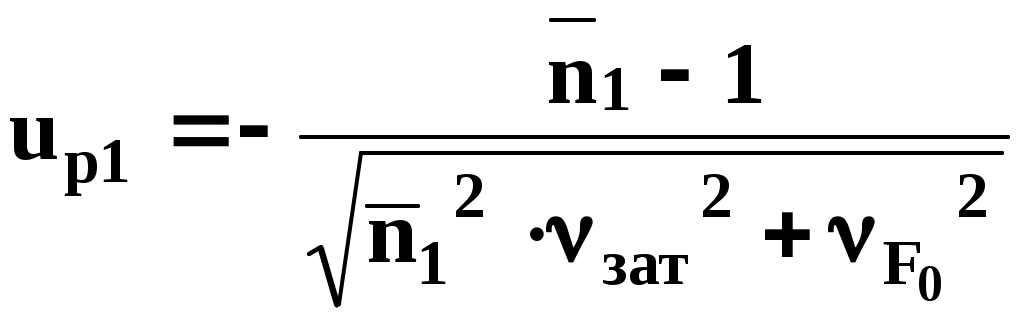

; _,

где , - средние значения затяжки и растягивающей силы;

, - коэффициенты вариации соответственно и .

=

где - напряжение от силы затяжки;

- предел текучести материала болта;

d_p – расчетный диаметр резьбы;

- коэффициент, учитывающий ослабление затяжки из-за

обмятия стыка, =1,1;

- коэффициент внешней основной нагрузки на стык.

Зависит от податливости детали и болта. =0,2-0,3.

Значение принимается в зависимости от метода контроля затяжки резьбового соединения:

Способ контроля	Динамометрическим ключом	По углу поворота гайки	По удлинению болта
	0,09	0,05	0,02

Значение коэффициента вариации растягивающей силы: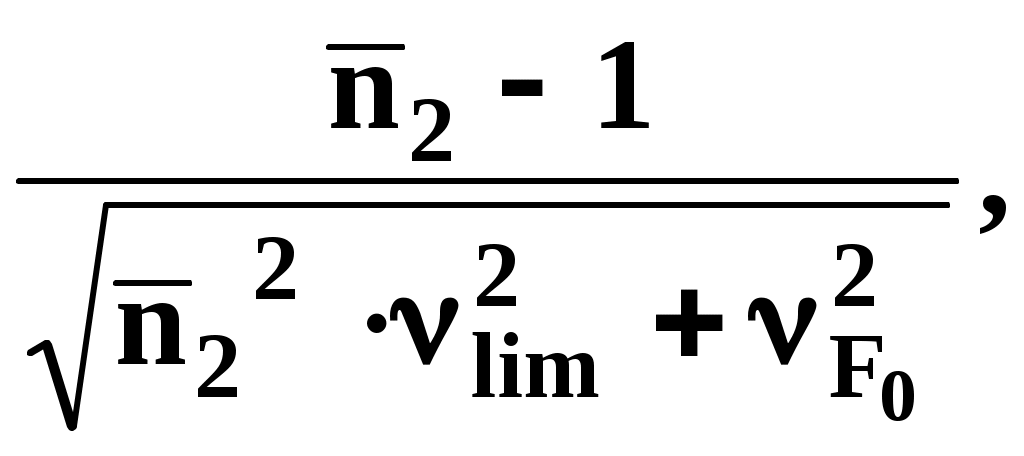

=0,1

u_p2=-

где - среднее значение коэффициента трения;

- среднее значение сдвигающей силы,



где - коэффициент вариации коэффициента трения определяется,

считая, что среднее квадратичное отклонение равно 1/6 части допуска.

u_p3=-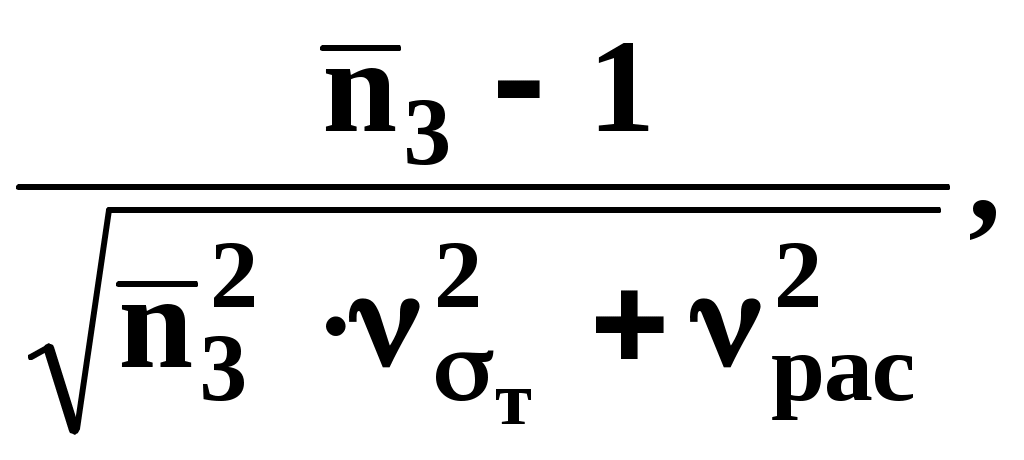

где k – коэффициент, учитывающий деформацию кручения болта

(k=1,3).

В технических расчетах принимаем .

u_p4=- ,

где - предел выносливости болта;

- действующие напряжения, приведенные к симметричном

циклу.

,

где - среднее значение предела выносливости гладкого образца;

- коэффициент влияния абсолютных размеров ( =1);

- среднее значение эффективного коэффициента концентрации напряжения, зависит от предела прочности материала

(Мпа)	400	600	800	1000
	3,0	3,9	4,8	5,2

Значение может быть вычислено: ,

где g – коэффициент чувствительности материала к концентрации

напряжений.

Для углеродистых сталей g=0,5-0,6.

Для легированных сталей g=0,7-0,8.

- среднее значение теоретического коэффициента концентрации напряжений. Зависит от шага резьбы и радиуса ее впадины.
,
где Р – шаг резьбы;

R– радиус впадины резьбы. Рассеяние радиуса впадины не зависит от точности резьбы и составляет (0,1-0,144)Р;

‑ коэффициент. Для стандартных болтов и гаек =1; для соединений типа стяжек =1,5-1,6.

‑ коэффициент технологического упрочнения.

Для нарезанной резьбы =1; для накатанной резьбы =1,2-1,3.

,

где - среднее значение максимальной нагрузки цикла;

0,5 - среднее значение амплитуды нагрузки. ;

- коэффициент чувствительности материала к асимметрии цикла

( =0,1);

- коэффициент вариации напряжения ;

- коэффициент вариации предела выносливости;

,

- коэффициент вариации предела выносливости детали одной

плавки, =0,06-0,08;

- коэффициент вариации среднего предела выносливости по

плавкам, 0,08;

- коэффициент вариации эффективного коэффициента

концентрации напряжений;

- коэффициент вариации концентрации напряжений

.
10.2. Расчет надежности сварных соединений
Предел выносливости сварных соединений имеет значительное рассеяние. В стыковых соединениях, например, от разброса угла шва рассеяние составляет 30% для ручной и 20% для автоматической сварки. Сварка лобовыми швами соединения внахлестку дает рассеяние предела выносливости в 35%. В тавровых соединениях рассеяние предела выносливости достигает 23%. Для сварных коробчатых балок с большим числом швов и непроваром корня швов рассеяние достигает 30-40%.

Т.о. можно установить коэффициент вариации предела выносливости вследствие разброса качества сварного шва

стыковая сварка ручная	0,05
стыковая сварка полуавтоматическая или автоматическая	0,03
внахлестку	0,06
в тавр с разделкой кромок и глубоким проплавлением	0,04
в тавр без разделки кромок и проплавления	0,06
с элементами, не передающими нагрузки	0,03
балки двутавровые	0,05
коробчатые балки	0,09

При наличии окалины коэффициент вариации, вызванный только некачественным состоянием поверхности – 0,06.

Коэффициент запаса прочности

где ‑ среднее значение предела выносливости;

‑ среднее значение действующих напряжений.

‑

‑ среднее значение предела выносливости для гладкого образца;

‑ коэффициент влияния абсолютных размеров;

‑ коэффициент, учитывающий упрочнение 1;

‑ коэффициент, учитывающий состояние поверхности; 1;

‑ эффективный коэффициент концентрации напряжения.



‑ коэффициент вариации предела выносливости сварной детали;

‑ коэффициент вариации нагрузки.



‑ коэффициент вариации предела выносливости детали одной плавки без сварного шва, =0,04-0,06;

‑ коэффициент вариации среднего предела выносливости по плавкам, =0,06-0,08;

‑ коэффициент вариации предела выносливости в зависимости от состояния поверхностей свариваемых деталей. Без окалины, кромки не повреждены, =0 или =0,06 (при наличии окалины или поврежденных кромок).