Конспект_СвСУ. Конспект лекций для студентов специальности 153 01 07 Информационные технологии и управление в технических системах

• Название: Конспект лекций для студентов специальности 153 01 07 Информационные технологии и управление в технических системах
• Анкор: Конспект_СвСУ.docx
• Дата: 09.09.2018
• Размер: 8.24 Mb.
• Имя файла: Конспект_СвСУ.docx
• Тип: Конспект лекций; #24302
• страница: 39 из 42

6.1 Цифроаналоговые преобразователи

Выделяют

1 Принцип суммирования напряжений (см. рисунок 6.1, а).

Имеется цифровой код, который следует преобразовать в аналоговую форму. По горизонтальной оси откладывается заполнение счетчика прямого счета (см. рисунок 6.1, б), по вертикальной оси – ступени, кванты, которые в идеале можно представить в виде наклонной прямой, аналоговой по природе. Это может быть не прямая, а произвольной формы линия в том случае, если вес кода не как у счетчика прямого счета, а произвольный.

Из построения видно, что прямая выходит не с начала координат. Это погрешность преобразования. Можно прямую провезти через углы квантов, тогда погрешности не будет. Но обычно при фильтрации выделяются средние части квантов, и есть начальная погрешность, которую часто устраняют балансировкой, применяющейся совместно с подобными схемами.



Рисунок 6.1 — Принцип суммирования напряжения, а); цифровое преобразование, б)

Выделяют линейную и нелинейную погрешности (см. рисунок 6.2).

Рисунок 6.2 — Линейная погрешность, а); нелинейная погрешность, б)
Выделяют шум квантования. Чем меньше ступеньки, тем меньше шум квантования. Можно фильтровать его, но это снижает быстродействие преобразования.

В схеме рисунка 6.1, а) ключи замыкаются и размыкаются соответственно нулями и единицами кода. При этом происходит суммирование соответственно разрядов и квантов.

Достоинство: несложность идеи, но метод не применяется, так как большое количество источников трудно реализуемо.

2 Принцип суммирования токов (см. рисунок 6.3).



Рисунок 6.3 — Типовое включение ОУ по инвертирующей схеме, а);

эквивалентная схема включения схемы а), б); суммирование токов, в)
Смысл схемы, представленной на рисунке 6.3, б), заключается в том, что точка 1, соответствующая верхнему электроду ОУ (схема 6.3,а), заземлена, потому что здесь действует глубокая ООС по напряжению. Она сводит сопротивление между “–” и “+” входами, а также R2 почти к нулю. Из данной схемы можно сделать выводы:

1 Точка 1 заземлена, следовательно, источник сигнала Е_с через R1 работает на землю, а выход источника Е_вых через R_ос также на землю, т. е. они как будто независимы.

2 Так как реально в схеме рисунка 6.3,а) сопротивление между “–” и “+” входами стремится к бесконечности, то тока в проводнике между точкой 1 и землей в схеме 6.3,б) почти нет. А это означает последовательное соединение R1 с R_ос; токи I₁ и I_ос равны, следовательно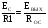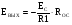





Это типовая формула коэффициента усиления инвертирующего включения ОУ.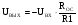



Здесь уместно вспомнить пять идеальных свойств операционных усилителей:

а) R_BX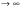

б) K_U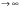

в) полоса частот стремится к бесконечности;

г) выходное сопротивление стремится к нулю;

д) входные и выходные напряжения в режиме ожидания равны нулю.

Разработчики операционных усилителей в интегральном исполнении стараются удовлетворить эти свойства. Именно по этой причине ток в цепи: 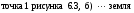практически равен нулю. Получается двойственность подхода к точке 1. С одной стороны она заземлена. С другой стороны не соединена с землей, т.е. имеется разрыв в цепи .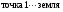

В схеме, изображенной на рисунке 6.3, в), два источника сигнала. Покажем, что в этой схеме суммируются токи, а через них и напряжения со своими коэффициентами усиления.

Так как точка 1 с одной стороны замкнута накоротко на землю, а с другой стороны имеет бесконечное сопротивление, в идеале, по отношению к земле, то сумма токов I₁ и I_2– равна току I_ос: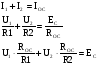



Из последней записи следует, что складываются напряжения со своими коэффициентами усиления. На этом принципе суммирования токов, а следовательно и напряжений, строится ЦАП. Их отличительными особенностями являются:

а) наличие ОУ;

б) у этого ОУ используется инвертирующий вход.

Выделяют

– ЦАП с весовыми резисторами;

– ЦАП с матрицей R–2R.
6.1.1 ЦАП с весовыми резисторами
Весовые резисторы – это означает, что сопротивление каждого резистора, их “вес” соответствует “весу” цифрового кода, так же как и точность исполнения. Наименее точные резисторы младших разрядов, наиболее точные – старших. В интегральном производстве вес резистора уточняют лазерной подгонкой. Здесь, для примера, принимаем всего четыре разряда двоичного кода:

1 001

2 010

3 011

4 100

Примем также, что верхнее положение переключателей k1, k2, k3 (см. рисунок 6.4) соответствует единице в кодах 1, 2, 4. В коде 3 две единицы, поэтому, k1, k2 в верхнем положении, а k3 – в нижнем.


Рисунок 6.4 – ЦАП с весовыми резисторами

Примем U_вх=E₀=1 В, R_ос=50 кОм, U_вых старшего разряда кода равным 10 В.

Рассчитаем величины резисторов R1, R2, R3:

1–ый код R1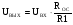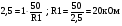

; ;

2 ;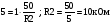

4 .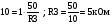

Для третьей позиции рассчитаем необходимую величину сопротивления резистора таким же образом, получится 6,66 кОм. И если установить в верхнее положение переключатели k1, k2 (k3 – нижнее) в соответствии с третьим кодом (011) и рассчитать величину параллельного соединения R1=20 кОм и R2=10 кОм, то получится тоже 6,66 кОм. Следовательно, получаем на графике лесенку (см. рисунок 6.4). Из схемы следует, что внутреннее сопротивление источника сигнала +E₀ должно быть минимальным (почти нулевым) для уменьшения погрешности преобразования (суммирования).

Чем старше разряд кода, тем точнее должен быть соответствующий резистор (например, R3 на рисунке 6.4). На “лесенке” рисунка 6.4 этому резистору соответствует цифра 10 В, а также ступенька такой же величины, как и для младшего разряда. Но если резисторы R1…R3 будут иметь одинаковую погрешность, то ясно, что ступенька старшего разряда может быть значительно большей в сравнении со ступенькой младшего разряда. Следовательно, чем старше разряд, тем выше точность резисторов. Таким образом, различие величин резисторов, а также их точностей принято называть недостатками этого вида схем. Тем не менее, они широко применяются в интегральной схемотехнике.
6.1.2 ЦАП с матрицей R–2R
Схема матрицы R–2R изображена на рисунке 6.5.

Рисунок 6.5 – Матрица R–2R
Матрицам R–2R присущи два основных свойства:

– делит напряжение Е₀ по двоичному закону;

– обладает неизменным сопротивлением, равным 2R, независимо от количества входящих элементов.

На рисунке 6.6 приведены две схемы преобразователей на основе матрицы R–2R.





Рисунок 6.6 — ЦАП с суммированием токов, а);

ЦАП на основе принципа деления напряжения, б)

В схеме, изображенной на рисунке 6.6, а), производится суммирование напряжений со своими коэффициентами усиления (как это следует из принципа суммирования токов), причем напряжения представлены деленными по двоичному закону. Используется минус–вход ОУ, так как применено суммирование токов.

В схеме на рисунке 6.6, б) не производится суммирование токов, поэтому в качестве входа ОУ – плюс–вход. Можно вообще без ОУ, если вход, например, осциллограф (у которого большое входное сопротивление) или нагрузки почти нет.

При нижнем положении ключей боковые 2R резисторы на земле, что соответствует принципу матрицы R–2R. При верхнем положении на Е₀, следовательно, внутренне сопротивление Е₀ должно быть почти нулевым для уменьшения погрешности преобразования. Из внешнего вида схемы не просматривается наглядность принципа деления напряжения. Тем не менее производится ЦАП–преобразование.

Для доказательства принципа деления напряжения в схеме рисунка 6.6, б) проанализируем два фрагмента этой схемы, изображенных на рисунке 6.7, а), б)


Рисунок 6.7 – Фрагменты матрицы R–2R в схеме рисунка 6.6, б)
Первый фрагмент (рисунок 6.7, а) имеет место при верхнем (замкнутом) положении переключателя S1, остальные переключатели S2, S3 в нижнем положении (замкнуты). Ясно, что в этом случае выходное напряжение матрицы равно 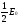, т.е. поделено на две равные части, что и требуется по двоичному закону, как в схеме рисунка 6.6, а). Второй фрагмент соответствует верхнему положению ключа S2, остальные ключи на земле. Покажем, что здесь, на выходе будет ¼ напряжения E₀. Для этого представим схему рисунка 6.7, б) так, как на рисунке 6.7, в). 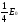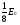Проведя простейшие расчеты, убеждаемся, что действительно, выходное напряжение схемы 6.7, в) равно .Если перевести в верхнее положение только S3, а S1, S2 в нижнее положение, то на выходе будет и т.д.

6.1.3 ЦАП с сигма–дельта модуляцией
Это имульсный класс интегральных преобразователей (рисунок 6.8). Слово “сигма” – сумма, “дельта” – схема работает на импульсном принципе.


а)


б)
Рисунок 6.8 — Схема сигма–дельта модулятора, а); графики процессов преобразования (ЦАП), б)

На вход подается сигнал h(t) (график 1 рисунка 6.8,б). Элементом 1₁ с инверсией производится преобразование, как на втором графике на рисунке 6.8, б). Тактовый сигнал с одной стороны подается на нижний вход &₁, верхний &₂; с другой стороны проинвертированный инвертором 1₂ на ключ S3 (графики 3, 4). Выходы логических элементов &₁, &₂ выдают импульсы, представленные пятым и шестым графиками на рисунке 6.8, б), которые управляют ключами S1 и S2. На выходе ключей S1 и S2 включен конденсатор С1, емкость которого в тысячи раз меньше емкости С2 интегратора на ОУ.

Через ключи S1 и S2 происходит заряд С1 малой величины от источников +В или –В, соответствующей полярности. Замыкается ключ S3, передает заряд конденсатора С1 в С2. Заряд на С1 представлен седьмым графиком рисунка 6.8, б), а заряд С2 соответственно – восьмым графиком. Из восьмого графика следует, что импульсы сигнала первого графика преобразуются в аналоговый сигнал восьмого графика, т.е. осуществляется операция ЦАП. Достоинства схемы – несложность, высокая точность преобразования, стабильность.
6.1.4 ЦАП с прямым преобразованием
Отличаются несложностью схем, однако имеют невысокую точность преобразования. Один из вариантов прямого преобразования на рисунке 6.9.



Рисунок 6.9 — ЦАП с прямым преобразованием
В схему вводится реверсивный счетчик, в котором периодически (циклически) параллельным образом записывается цифровой код. На протяжении действия цикла на счетчик, работающий в режиме вычитания (реверсивного считывания) поступают тактовые импульсы f_T, следовательно, на выходе счетчика выводятся импульсы, количество которых определяется цифровым кодом, записанным параллельным образом. Интегратор считает эти импульсы, на его выходе выделяется аналоговое напряжение, пропорциональное записанному в счетчике коду. Один из серьезных недостатков этого принципа – цикличность. Т.е. преобразователь не учитывает того, что происходит с сигналом на протяжении действия части цикла. Другие недостатки – невысокое быстродействие, большая погрешность.