Конспект лекций по дисциплине гидросиловые установки и возобновляющиеся источники энергии для студентов, обучающихся по специальности
 Скачать 6.68 Mb.
|
|
Рис. 11.4. Регулирование расхода иглой Размеры лопастей рабочего колеса ковшовой турбины обычно составляют: а = (2,8÷3,6)dс, с = (2,5÷2,8)dс и е = (0,9÷1,0)dс. Для опирания всех частей ковшовой турбины служит корпус, а для защиты от разбрызгивания воды — кожух, которые на рис. 11.3 не показаны. Лекция 12. Параметры работы гидротурбин — напор, расход, мощность, коэффициент полезного действия. – Понятие о характеристиках гидротурбин, их подобии и моделировании. – алгоритм подбора гидротурбин при проектировании гидроэлектростанций Режим работы турбины определяется геометрическими и кинематическими показателями. Геометрические: форма проточной части, то есть тип турбины, ее размер (диаметр D1) и открытие направляющего аппарата (НА) или иглы a0; у ПЛ турбин еще и угол установки лопастей рабочего колеса φ. Кинематические показатели связаны с условиями гидравлического подобия режимов и выражаются зависимостями от напора H или расхода Q:  или  ,где n – частота вращения, H = напор, η – гидравлический кпд турбины. Параметры режимов могут быть выражены: для жестколопастных турбин для поворотно-лопастных турбин функциями 4-х переменных: функциями 5-ти переменных: N = fN(D1, a0, H, n); N = fN(D1, a0, φ, H, n); Q = fQ(D1, a0, H, n); Q = fQ(D1, a0, φ, H, n); η = fη (D1, a0, H, n); η = fη (D1, a0, φ, H, n); HS = fHS (D1, a0, H, n); HS = fHS (D1, a0, φ, H, n); здесьN – мощность турбины, HS– допустимая высота отсасывания. Разделение на функции и независимые переменные условно – их можно поменять местами. Вместо Hвсе функции можно записать в зависимости от Q, например, η = fη(D1, a0, Q,, n). Однако при проектировании напор обычно задается, а расход вычисляется, и поэтому функции от H удобнее. Поскольку одновременное графическое изображение функций 4-х или 5-ти переменных невозможно, для практических целей часть переменных принимаются постоянными и используют характеристики типа y=f(x), называемые линейными, и типа z=f(x,y), называемые общими. Особое место среди общих характеристик занимает универсальная (оборотно-расходная) характеристика (рис. 12.1), определяющая свойства турбин данного типа. Она строится при D1 = const= 1 м и H= const = 1 м в поле так называемых приведенных (единичных) параметров  , где  и  . Универсальная характеристика обычно включает семейства изолиний гидравлического кпд  , открытий направляющего аппарата  и коэффициента кавитации  , но может содержать изолинии и других параметров.Получают универсальную характеристику по результатам испытаний моделей турбин на энергетических или кавитационно-энергетических стендах, и показанные на ней значения η, a0, σ относятся к модели. Поэтому на характеристике обязательно указывается размер модели D1m. Указывается также напор, при котором проведены испытания, и приводится габаритный чертеж турбины, включая спиральную камеру и отсасывающую трубу. 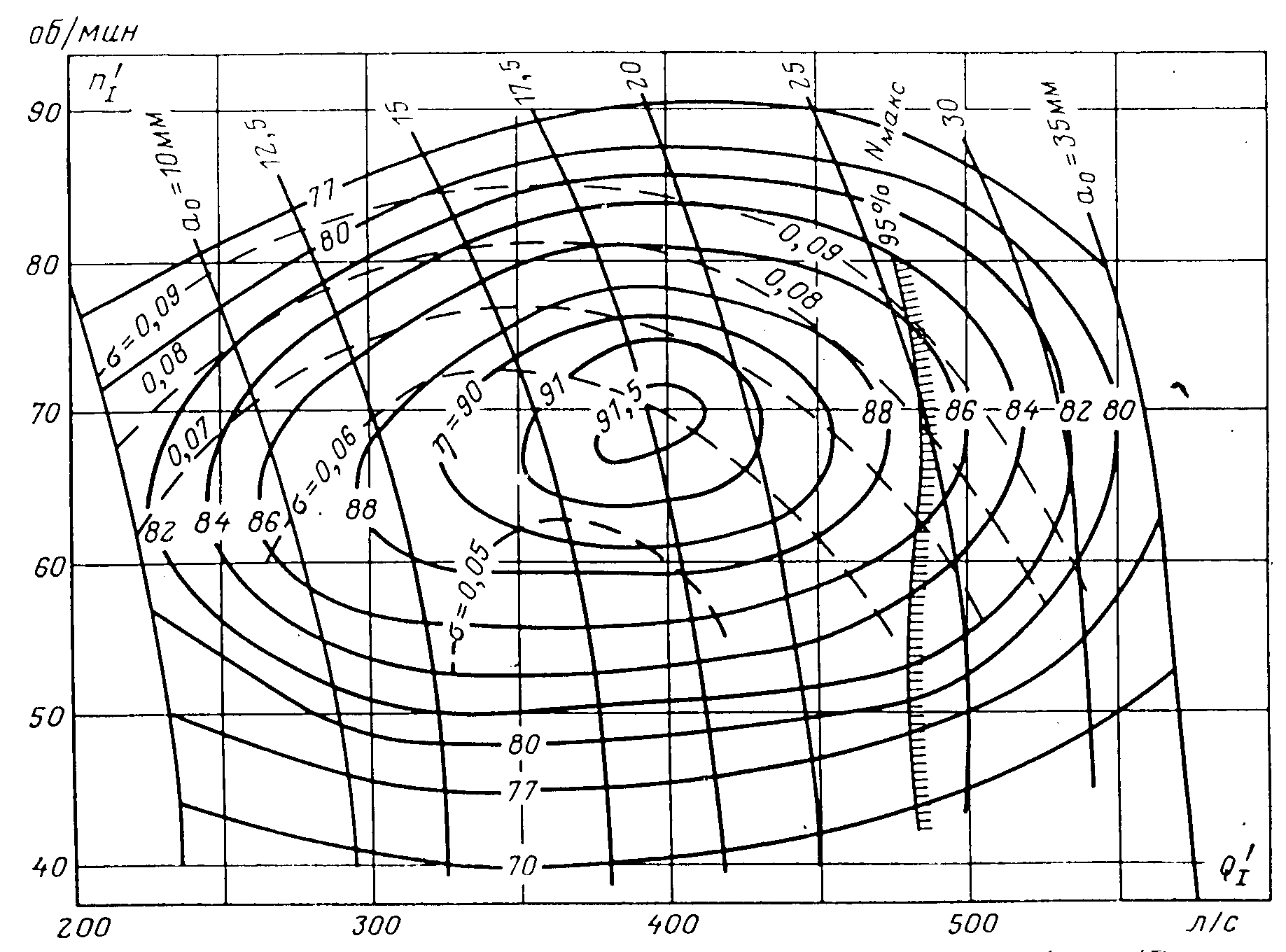 Рис. 12.1. Универсальная характеристика радиально-осевой турбины (Dм = 460 мм, Н = 4 м) Общие характеристики при D1=const и n=const именуются эксплуатационными и представляют собой отображения универсальной характеристики в поле координат N-HилиQ-H. Напорно-мощностная характеристика представляет собой семейства изолиний η = fη(N, H) иHS = fHS(N, H) в поле N-H (рис. 12.2). Область рабочих режимов выделена линиями со штриховкой. Вертикальная прямая представляет ограничение по мощности Nтурб.макс = Nген. ном / ηген и соответствует номинальной активной мощности генератора. Наклонная линия со штриховкой –ограничение по открытию, соответствующее максимальной мощности турбины при максимальном открытии НА и напорах меньше расчетного*. Напорно-расходная характеристика представляет семейства изолиний η = fη(Q, H) иN = fN(Q, H) в поле Q-H (рис. 12.3). Линии, ограничивающие область рабочих режимов, имеют тот же смысл, что и на рис. 12.2. Пересекаясь при расчетном напоре, они показывают максимальное значение расхода турбины. На эксплуатационные характеристики могут наноситься и другие семейства изолиний, кроме показанных, например, амплитуды пульсаций давления.  Рис. 12.2. Эксплуатационная напорно-мощностная характеристика турбины 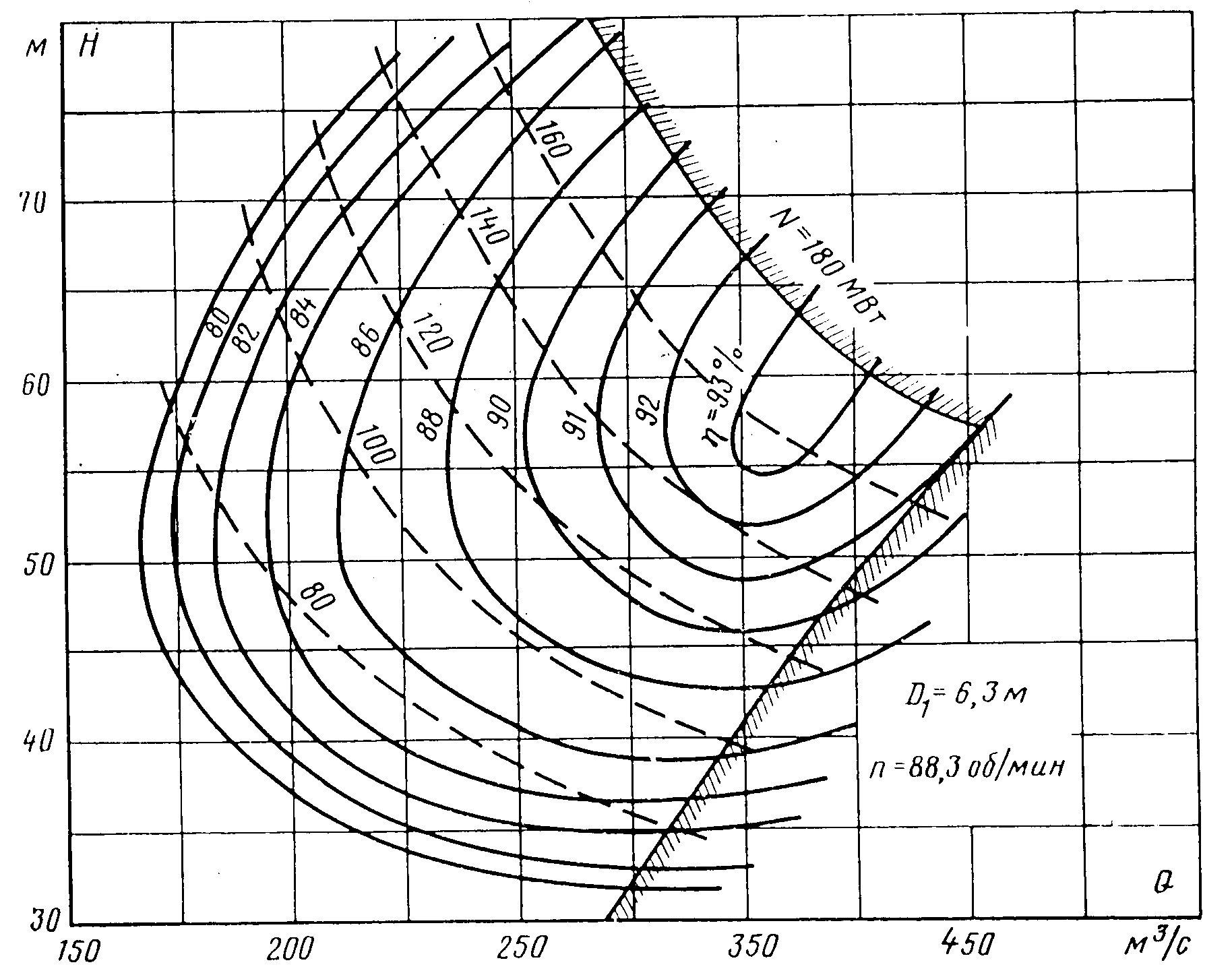 Рис. 12.3. Эксплуатационная напорно-расходная характеристика турбины 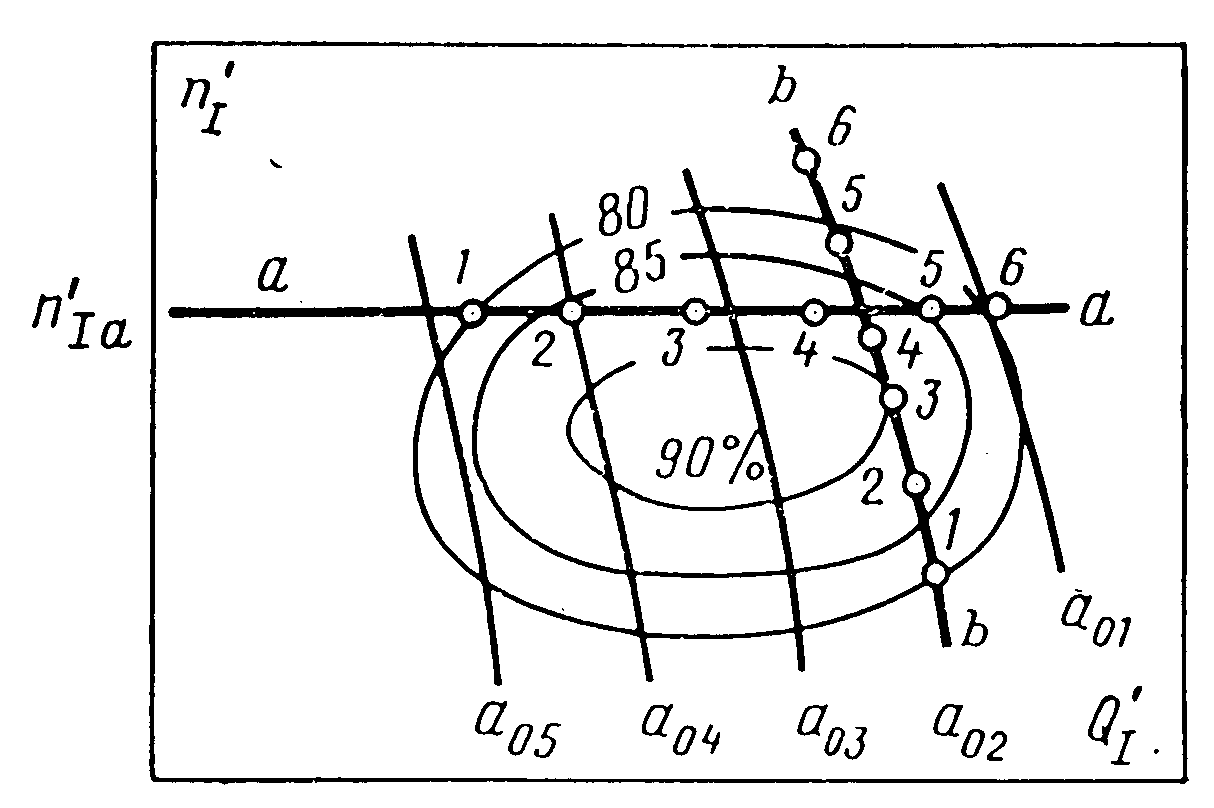 Рис. 12.4. К построению линейных характеристик по универсальной Координаты H, Q, N получают из приведенных параметров по формулам пересчета  , , .Приведённая частота вращения турбины  =  +  больше приведенной частоты модели на значение постоянной поправки .Линейные характеристики строятся как функции y(x) при трех постоянных параметрах, один из которых, как правило, диаметр D1. Например, линейные расходная и мощностная характеристики представляют собой сечение универсальной характеристики горизонтальной прямой a-a (рис. 12.4) при постоянном значении приведенной частоты вращения  , то есть при постоянных D1, n и H.В нескольких точках этой прямой по универсальной характеристике определяются значения кпд модели м, открытия НА a0, приведенного расхода  , коэффициента кавитации . Затем для каждой из точек вычисляются значения расхода Q, кпд турбины т, мощности N и высоты отсасывания HS и строятся графики расходной характеристики N(Q), т(Q), a0(Q), HS(Q) или мощностной характеристики Q(N), т(N), a0(N), HS(N).Линейная напорная характеристика строится при постоянныхзначениях D1, n и открытия НАa0. Проводится сечение универсальной характеристики линией b-b дляa0=const (см. рис. 12.4) и в каждой из выбранных точек вычисляются кпд турбины т и напор по формуле 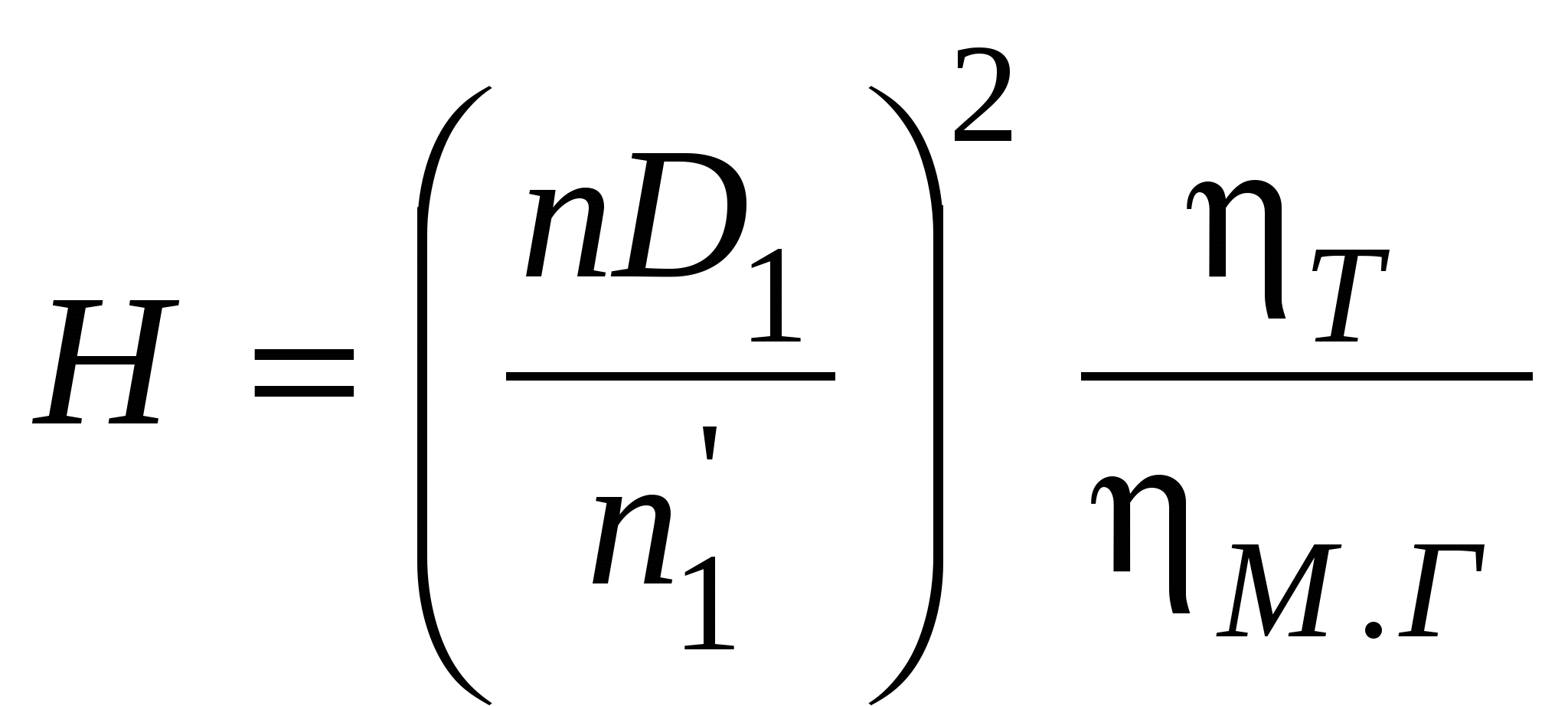 .Затем для каждой из точек вычисляются значения расхода Q, мощности N, высоты отсасывания HS и строятся графики напорной характеристики N(H), Т(H), HS(H) и другие. Линейная оборотная характеристика строится при постоянных значенияхD1, H и открытия НАa0. Проводится сечение универсальной характеристики линией b-b дляa0=const и в каждой из выбранных точек вычисляются кпд турбины т и частота вращения по формуле  .Затем для каждой из точек вычисляются значения расхода Q, мощности N и строятся графики оборотной характеристики N(n), Т(n) и другие. 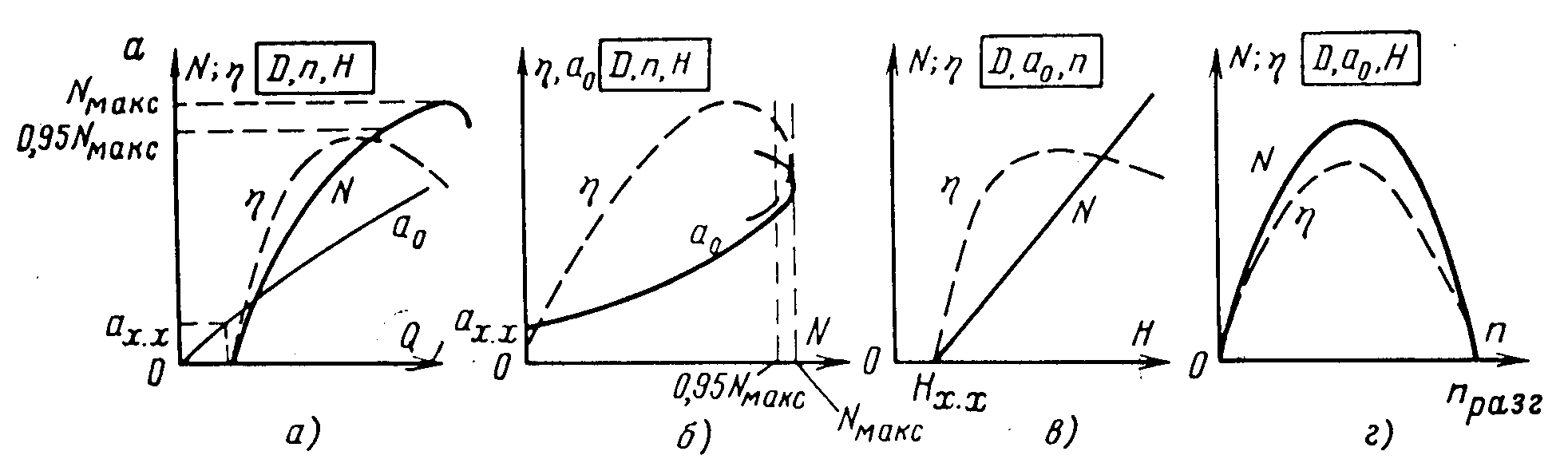 Рис. 12.5. Линейные характеристики турбины Общий вид рассмотренных линейных характеристик показан на рис. 5, где также отмечены точки открытия и расхода холостого хода, 95%-ного ограничения мощности (см. рис. 12.5, а и б), напора холостого хода (см. рис. 12.5, г) и разгонной частоты вращения (см. рис. 12.5, д). При проведении натурных испытаний гидротурбин с измерением расходов могут быть получены натурные линейные (так называемые рабочие) характеристики N(a0), hт(a0), Q(a0), Q(N), hт(N) и другие. Режимные точки, пересчитанные в координаты и нанесенные на универсальную характеристику, позволяют судить об идентичности модели и натурной турбины. Исходные данные, необходимые для подбора гидротурбин: расчетный, максимальный и минимальный напоры нетто, мощность ГЭС или одного агрегата, отметка нижнего бьефа. Подбор реактивных гидротурбин состоит из следующих этапов: Этап 1. Определение мощности одной турбины — NТ = NГЭС/m∙ген. Здесь m — число агрегатов на ГЭС; ген — КПД генератора (в первом приближении 0,97-0,98). Выбор типа турбины по максимальному напору и мощности с использованием номенклатурных графиков H – N. Этап 2. Вычисление расхода турбины QР=NТ/ 9,81HР∙ ηТ (кпд ηТ принимают для РО турбин 0,9…0,92, для ПЛ турбин — 0,87…0,9) при номинальной мощности NТ и расчетном напоре HР. Этап 3. Определение максимального приведенного расхода  по универсальной характеристике турбины в координатах . Для РО турбин значение приведенного расхода  принимается в точке пересечения горизонтальной прямой с ординатой  с линией 95%-ного ограничения мощности. Для ПЛ турбин значение приведенного расхода принимают по допустимой высоте отсасывания, то есть по максимальному значению коэффициента кавитации.Этап 4. Определение диаметраD1 с использованием формулы для приведенного расхода 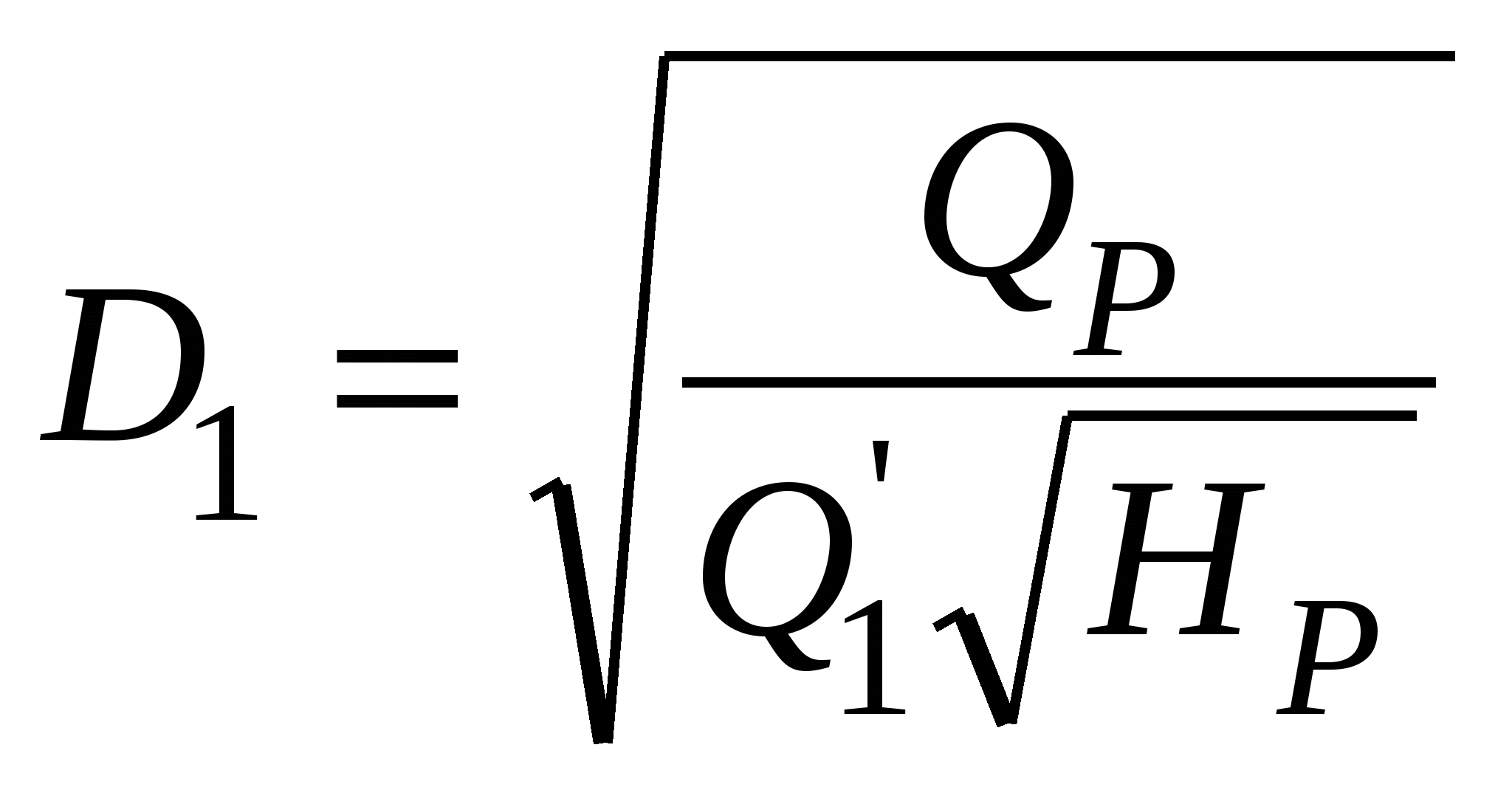 . Полученное значение диаметра округляют до ближайшего номенклатурного.Этап 5. Определение частоты вращения турбины с использованием формулы для приведенной частоты вращения  . Отсюда  . Расчетное значение приведенной частоты вращения принимается для РО турбин при , для ПЛ турбин — при +5…10 мин-1. Принимают ближайшее значение синхронной частоты вращения, определяемое по выражению nС=3000/р, где p — число пар полюсов ротора генератора.Этап 6. После назначения диаметра и частоты вращения следует построить на универсальной характеристике область рабочих режимов турбины и оценить, насколько эта область совпадает с областью максимальных кпд. По формуле вычисляют три значения приведенной частоты вращения — для расчетного, максимального и минимального напоров. Затем на характеристику наносят три горизонтальных линии  , соответствующие полученным значениям . Абсциссы , ограничивающие эти линии, определяются с учетом выбранного значения диаметра D1. Для расчетного напора  , по характеристике также определяется значение открытия направляющего аппарата a0макс. Для максимального напора  , где QHmax=NТ/ 9,81Hmax∙ ηТ. Абсцисса на линии  для минимального напора должна соответствовать такому же открытию направляющего аппарата a0макс, что и на линии максимального напора. Соединив определенные для трех напоров режимные точки с координатами , получим и оценим область рабочих режимов подобранной турбины (рис. 12.6). При неудовлетворительном результате подбор следует повторить, выбрав новые значения диаметра и частоты вращения.Этап 7. Вычисление минимально допустимой высоты отсасывания по зависимости 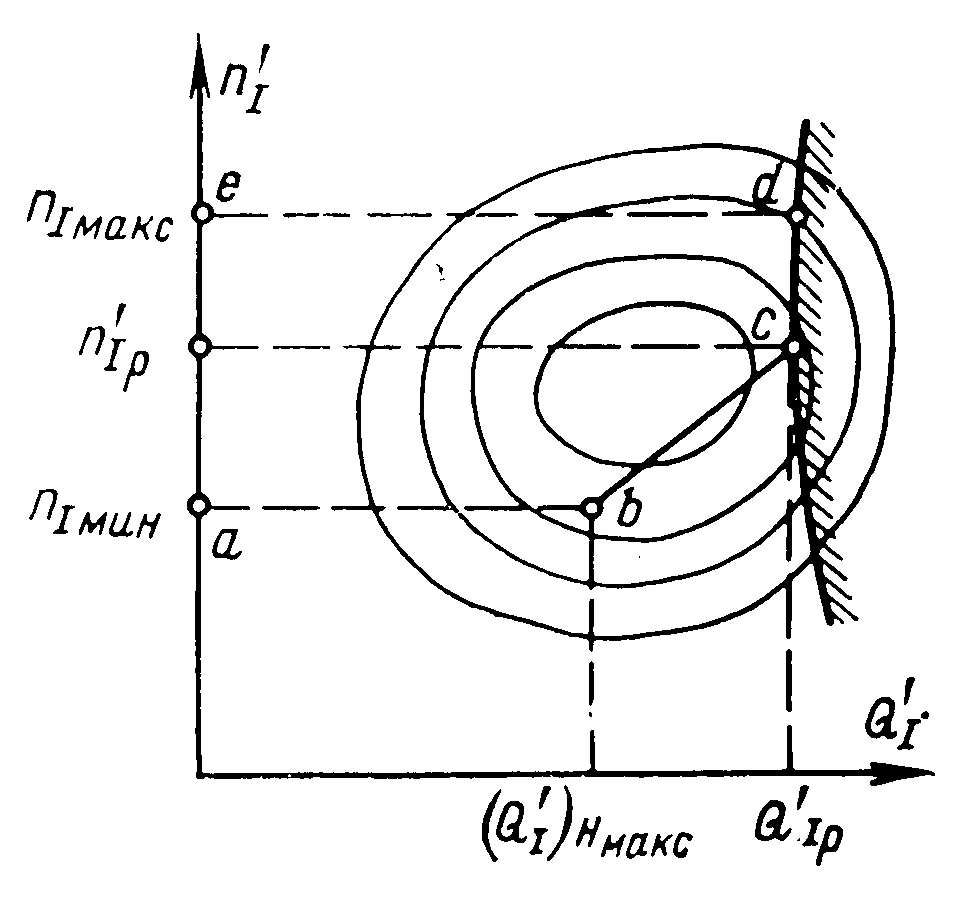 , Рис. 12.6. Используемая область характеристики турбины где НБ — отметка нижнего бьефа, — коэффициент кавитации, определяемый для нескольких (5-7) точек, покрывающих левую границу области рабочих режимов турбины. Напор в выбранных точках, если не известен заранее, определяется по формуле  . Из 5-7 вычисленных значений высоты отсасывания выбирается минимальная по абсолютному значению.Этап 8. Определение поправки на кпд турбины. Поправка на гидравлический кпд с учетом масштабного эффекта вычисляется по формуле  ,где г.м — максимальное значение кпд в оптимуме универсальной характеристики, ε — доля пересчитываемых потерь, принимаемая в первом приближении равной 0,75. В числителе подкоренных дробей — диаметр модельной турбины и напор при модельных испытаниях, в знаменателе — диаметр и напор подобранной турбины. В любой точке характеристики кпд турбины определяется зависимостью т = м + г – м.о, где м.о — поправка на механические и объемные потери, принимаемая равной 0,01-0,02. Этап 9. Определение размеров турбины по чертежам, прилагаемым к универсальной характеристике, где приводятся относительные размеры в долях от диаметра D1. Подсчет веса турбины и, отдельно, веса рабочего колеса по приближенным формулам или справочным таблицам, где вес определяется в зависимости от типа турбины, напора и мощности. Подбор ковшовых турбин имеет некоторые особенности. В частности, оптимальная приведенная частота вращения 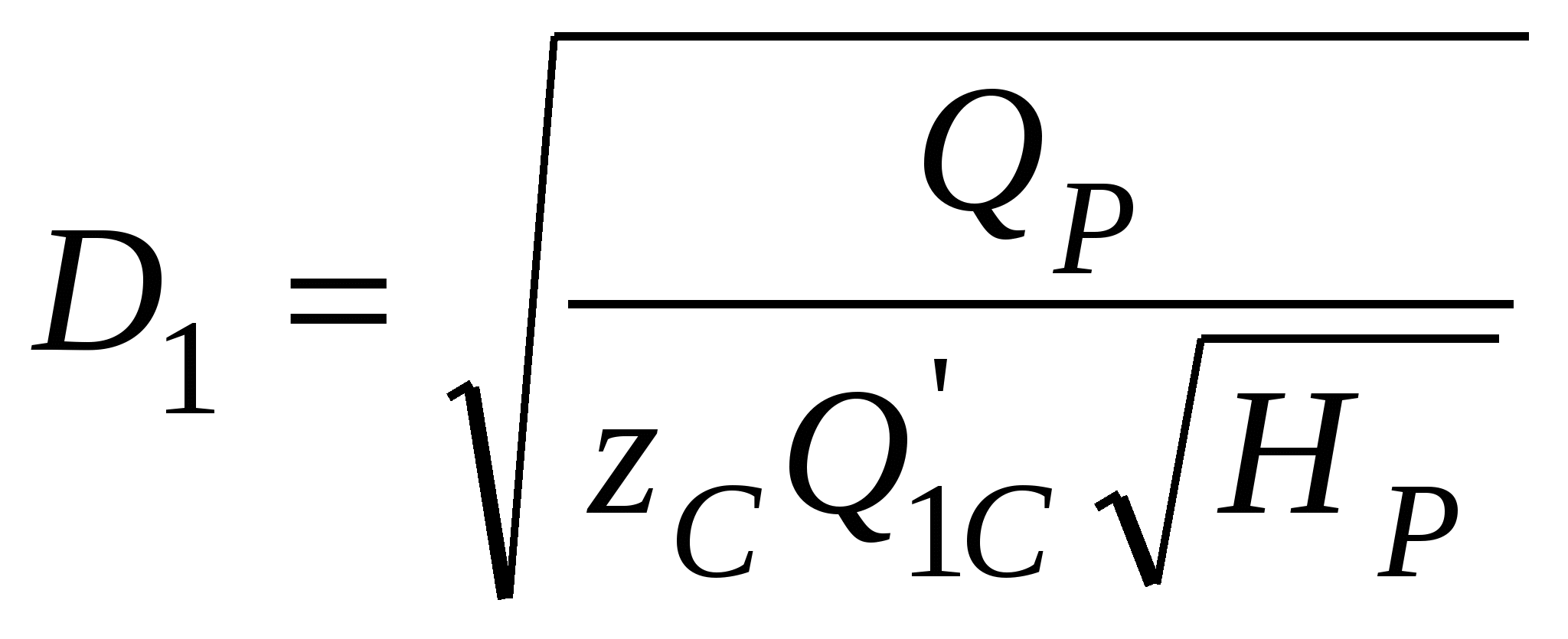для всех ковшовых турбин практически одинакова и составляет 39-40 мин-1. Диаметр турбины зависит от числа струй (сопл) zC и вычисляется по формуле ,где 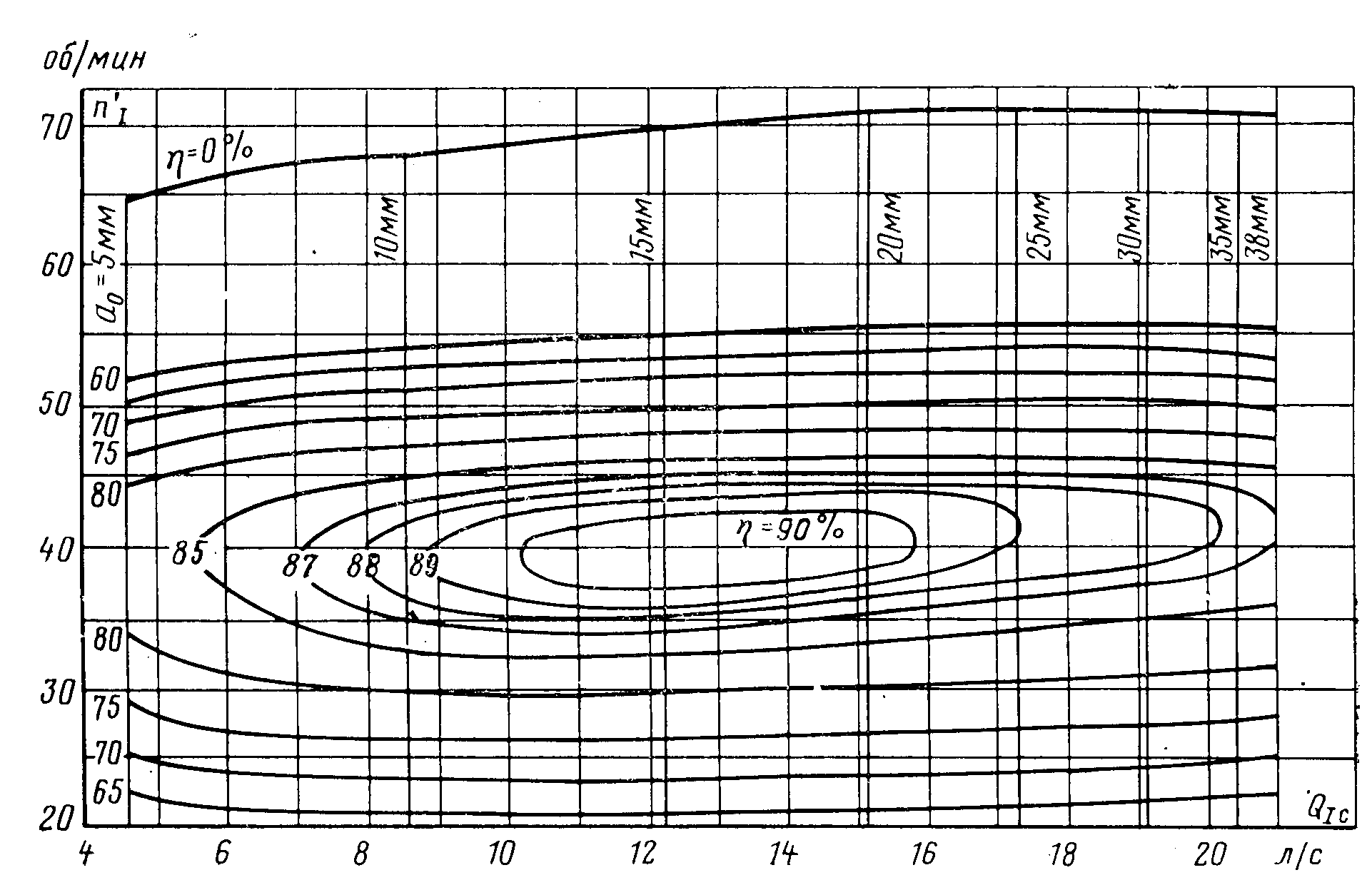 - приведенный расход одного сопла, определяемый по универсальной характеристике (рис. 12.7). Рис. 12.7. Универсальная характеристика ковшовой турбины (односопловая, число лопастей рабочего колеса 18) Частота вращения зависит от диаметра и, через диаметр, от числа сопл: 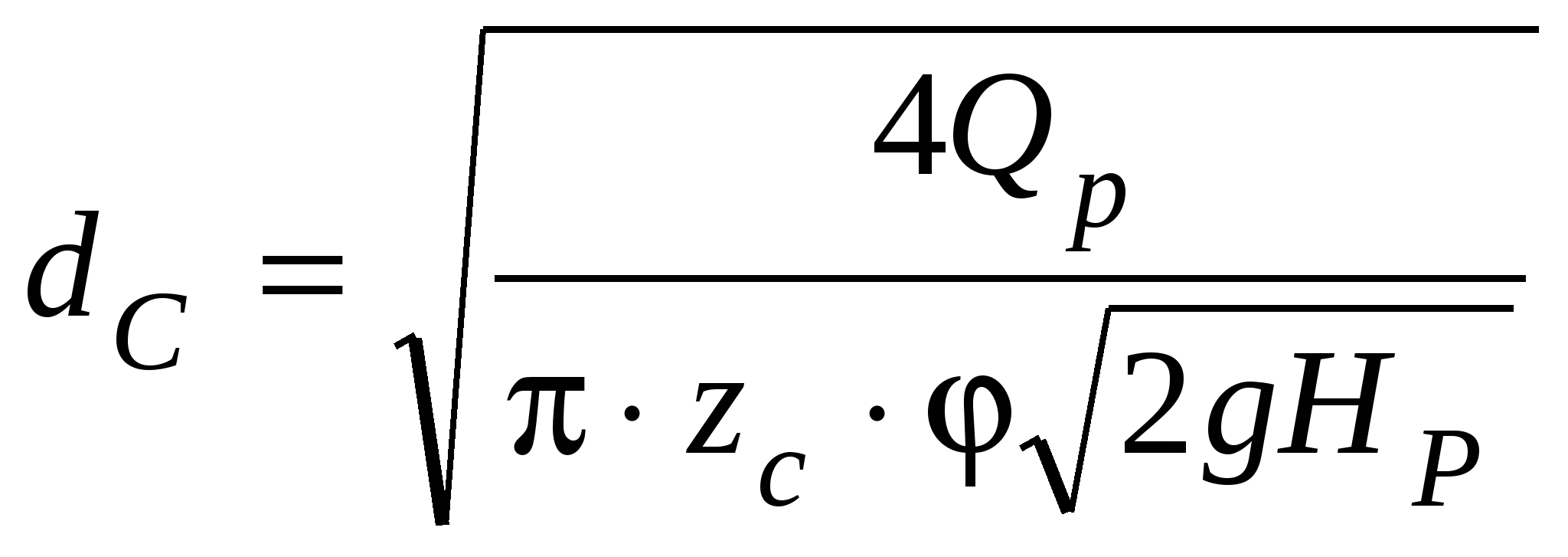 . Как правило, при подборе ковшовых турбин рассматриваются варианты с различным числом сопл — 1, 2, 3, 4, 6 и т. д. Строится таблица соответствия значений zC–D1–nи выбирается число сопл. Если синхронная частота вращения отличается от выбранного n, то следует изменить диаметр, чтобы сохранить  Принимая коэффициент скорости при истечении струи =0,98-0,99, вычисляют диаметр струи  , диаметр сопла dсопла= 1,3dC и наружный диаметр рабочего колеса DНАР=D1+ (2,8…3,6)dC.Лекция 13. Элементы проточного тракта гидротурбин — турбинные камеры и отсасывающие трубы, их типы, выбор формы и размеров. – Понятие о кавитации в гидротурбинах и коэффициенте кавитации Турбинная камера соединяет концевое сечение турбинного водовода и направляющий аппарат реактивной гидротурбины. К турбинным камерам предъявляются следующие требования: 1) равномерное по всему периметру (осесимметричное) питание направляющего аппарата; 2) гидравлические потери в самой камере, в статоре и при входе потока в направляющий аппарат должны быть малыми; 3) форма и размеры турбинной камеры соотносятся с условиями компоновки блока здания ГЭС. Важнейшее из этих требований обеспечивается в открытых безнапорных камерах (рис. 13.1, а), которые могут быть и напорными. Однако они имеют большие плановые размеры и поэтому применяются только на малых ГЭС. На крупных ГЭС применяются камеры, которые по всей своей длине или по ее части выполнены в виде спирали ("улитки"), с уменьшающимися по течению потока сечениями. Для крупных гидротурбин применяются только два типа турбинных камер — изготавливаемые из железобетона, с трапецеидальными поперечными сечениями и со спиральной частью, занимающей часть полной окружности выходного сечения камеры (периметра направляющего аппарата; изготавливаемые из стали, с круглыми поперечными сечениями, с так называемой "полной" спиралью, обнимающей весь периметр направляющего аппарата. Области использования турбинных камер со спиральными частями определяются главным образом напором. Бетонные (железобетонные) камеры применяются при напорах 4-80 м, а металлические при 40-700 м, рис. 13.2. Кроме турбинных камер со спиральными частями (спиральных турбинных камер), применяются также:
Конструкции турбинных камер. На рис. 13.3 показана стальная спиральная турбинная камера радиально-осевой турбины диаметром 5,5 м с напором 100 м. Входным сечением камеры считается сечение 0-0, перпендикулярное оси подводящего водовода. Концевое сечение принято определять по выходной кромке замыкающей колонны статора — зуба спирали. Камера почти полностью охватывает направляющий аппарат. Стальные спиральные камеры имеют угол охвата охв = 340÷350º. Поперечные сечения круглые; в концевой части, примерно на последних 90º, сечения переходят в эллиптические: необходимая площадь здесь настолько мала, что круглое сечение нельзя сопрячь с опорными поясами статора. 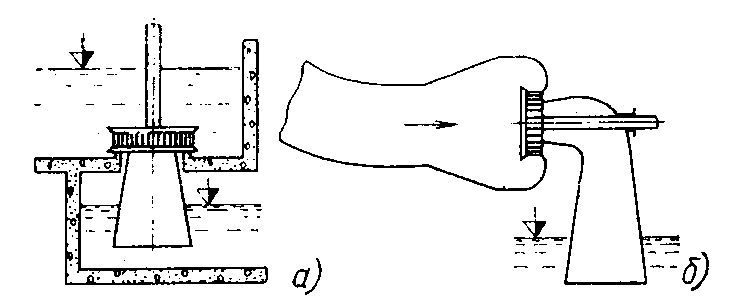 Рис. 13.1. Компоновки турбинных камер малых турбин 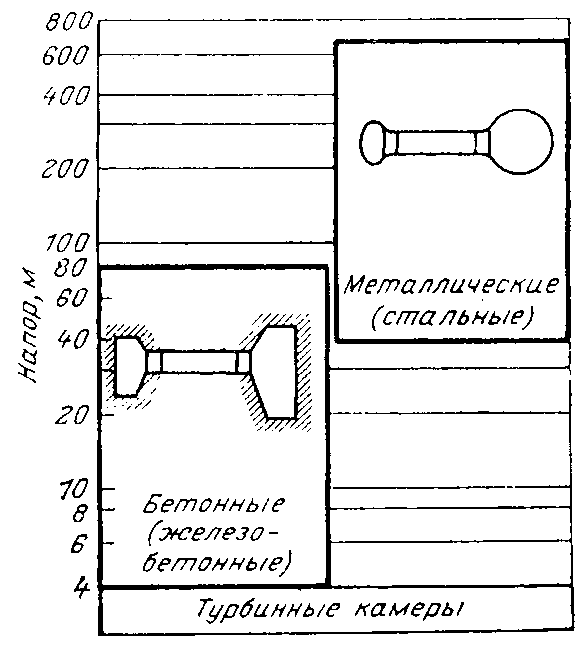 Рис. 13.2. Области использования спиральных турбинных камер по напору 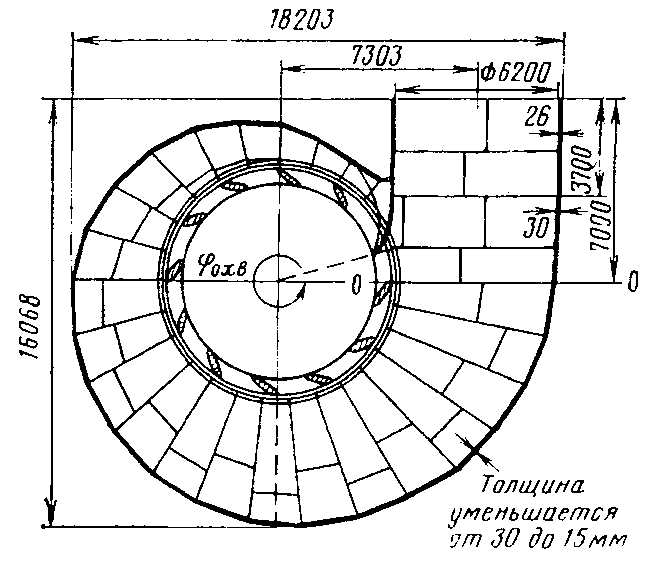 Рис. 13.3. Стальная турбинная камера Стальная спиральная камера представляет сварную конструкцию, выполненную из вальцованных стальных листов. Если камера имеет не слишком большие размеры (по транспортным условиям), то она может полностью изготавливаться на заводе литой или сварной конструкции, иногда объединенной со статором. Литые или цельносварные камеры применяются для турбин диаметром до 2,5 м. Оболочка стальной камеры рассчитывается на максимальное внутреннее давление воды с учетом гидравлического удара. При этом нужно исключить передачу нагрузки на бетон, для чего верхняя часть оболочки покрывается податливой прокладкой, например битумными матами, либо остается открытой. Наибольшее распространение получили конструкции спиральных камер с передачей части нагрузки от внутреннего давления воды на железобетон блока здания ГЭС. Бетонные турбинные камеры имеют трапецеидальную форму поперечного сечения и меньший угол охвата спирали, который составляет охв = 180÷270º и зависит от максимального напора Нмакс. Меньшие значения охв = 135º обоснованы необходимостью разместить статор турбины в середине блока здания ГЭС, т. е. условиями компоновки блока. Поперечные сечения бетонных камер (рис. 13.5) имеют трапецеидальную форму, высота b обычно больше, чем ширина а. Это делается с целью уменьшения габаритов камеры в плане и главным образом сокращения ширины Всп. 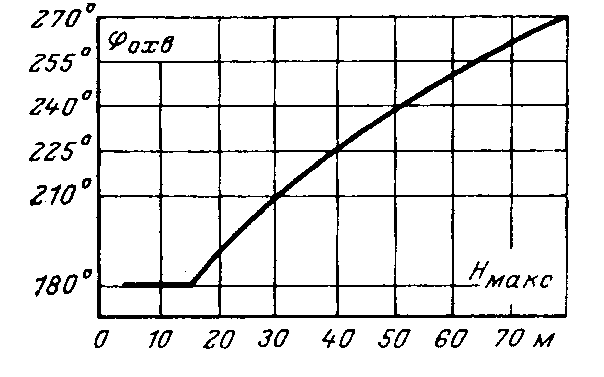 Рис. 13.4. Зависимость угла охвата бетонных спиральных камер от напора 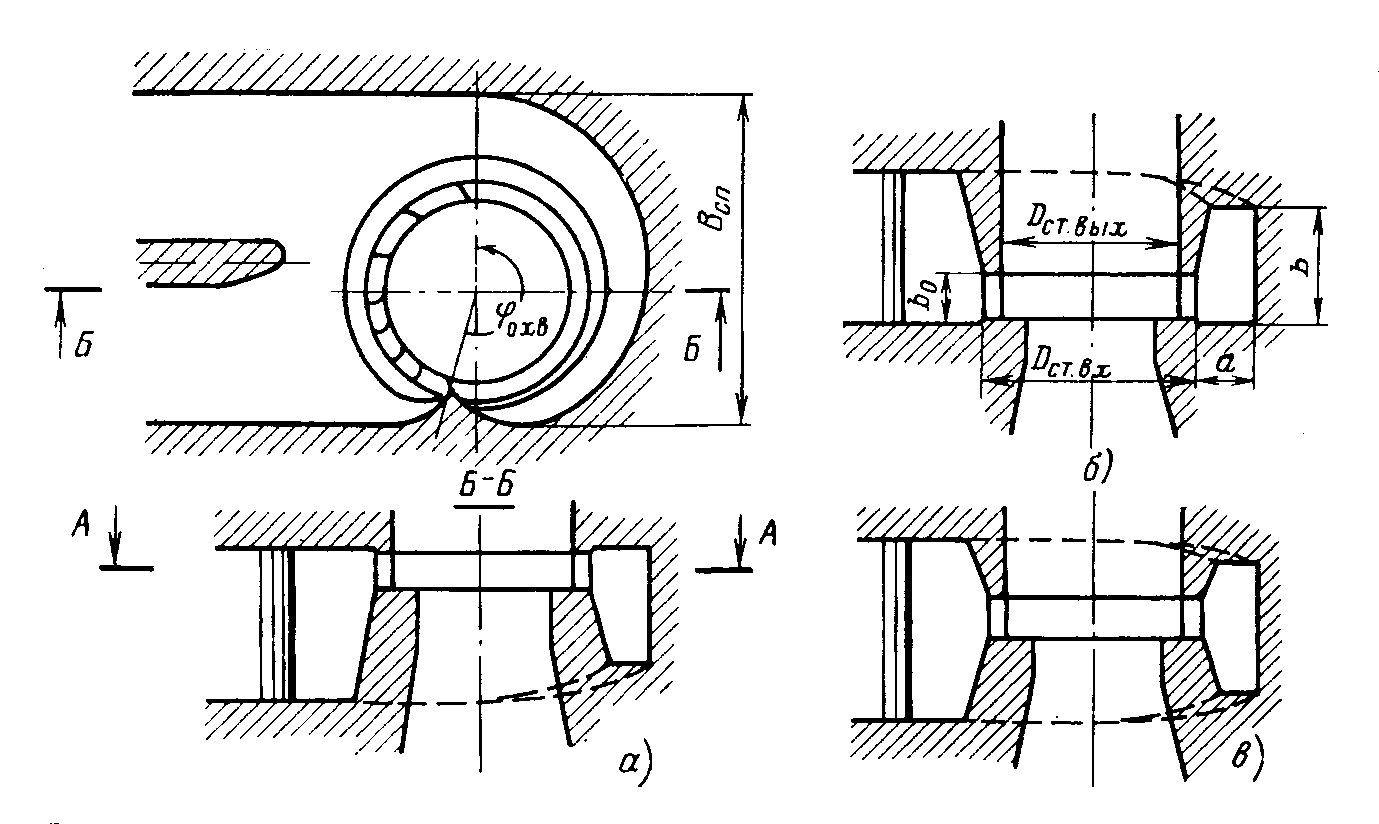 Рис. 13.5. Бетонные турбинные камеры Характерны три формы бетонных камер: развитая вниз с постоянной отметкой потолка (рис. 13.5, а); развитая вверх с постоянной отметкой пола (рис. 13.5, б); тавровая с переменной отметкой потолка и пола (рис.13.5, в). Выбор той или иной формы целиком определяется условиями наивыгоднейшей компоновки блока здания ГЭС. Значительная часть периметра направляющего аппарата при бетонных камерах получает воду непосредственно из подводящего водовода. Подвод воды к статору и направляющим лопаткам здесь менее благоприятен, так как при входе в статор и в направляющий аппарат происходит резкое изменение направления скорости. С целью улучшения условий входа потока в направляющий аппарат в правой четверти спирали перед зубом ставят криволинейные колонны, причем шаг их здесь делают меньше. При напорах более 50 м бетонные камеры снабжаются стальной облицовкой из листов толщиной 10-16 мм, которая служит противофильтрационной защитой, но учитывается при расчете конструкции на прочность. Она должна быть хорошо заанкерена в бетон. Конструкция и размеры турбинной камеры определяются заводом, поставщиком турбин, однако при проектировании ГЭС приходится рассматривать возможность изменения форм и размеров турбинных камер для лучшей увязки их с компоновкой блока здания ГЭС и со строительными конструкциями. Важным параметром является ширина турбинной камеры Всп. Относительное значение  в зависимости от Нр показано на рис. 13.6. 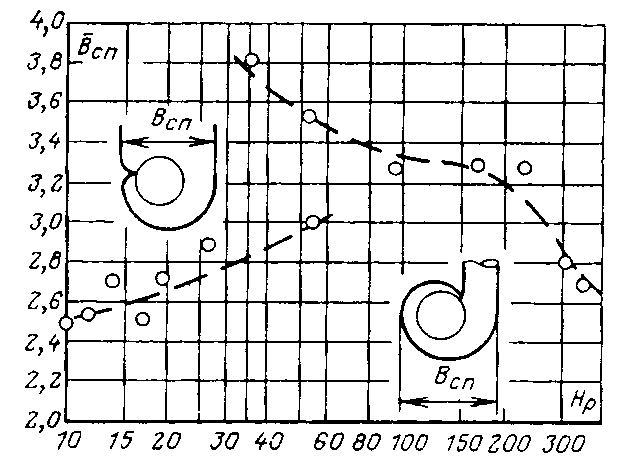 Рис. 13.6. Зависимость ширины турбинной камеры от напора Поскольку турбинная камера непосредственно примыкает к статорному кольцу, то необходимо знать его размеры, характеризуемые относительной высотой  и относительными диаметрами расположения входных и выходных кромок колонн  и  (см. рис. 13.5). Для турбин с бетонными камерами и ,бóльшие значения при D1 < 4,0 м. Для турбин со стальными спиральными камерами  и  ,бóльшие значения для D1 < 3,2 м. Для напоров выше 100 м оба диаметра увеличиваются на 0,03-0,07. Исходным положением для гидравлического расчета турбинной камеры является равномерное поступление расхода в статор и в направляющий аппарат по его периметру. Расход Q , проходящий через данное сечение спирали, определяемое углом (рис. 13.7), будет выражаться формулой  . (13.1)Здесь Q — полный расход турбины; — угол, отсчитываемый от конца зуба спирали. 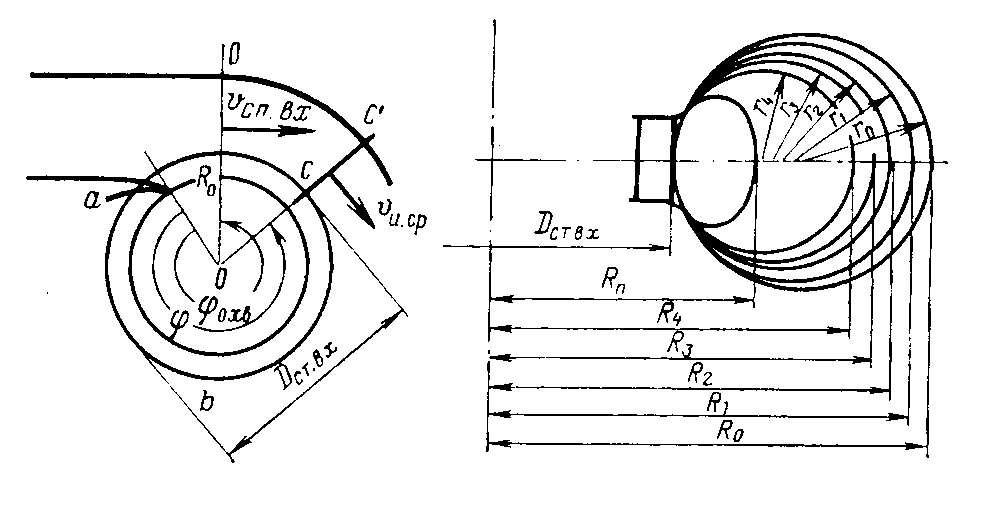 Рис. 13.7. К расчету металлической спиральной камеры Расход во входном сечении спиральной камеры равен:  .Размеры сечений спиральной камеры определяются на основании одной из двух гипотез: 1) по заданным значениям средней окружной компоненты скорости течения vu ср; 2) по заданному направлению скорости течения на выходном диаметре статора Dст.вых, т. е. непосредственно перед входом на направляющий аппарат. 1. Расчет по средним значениям скоростей производят либо по закону постоянства средней скорости vu ср = vсп.сх = const, где vсп.сх — средняя скорость во входном сечении спирали 0-0 (рис. 13.7), либо по закону убывающей средней скорости vu ср = f(), причем vсп.ср убывает с уменьшением по графику на рис. 13.8. 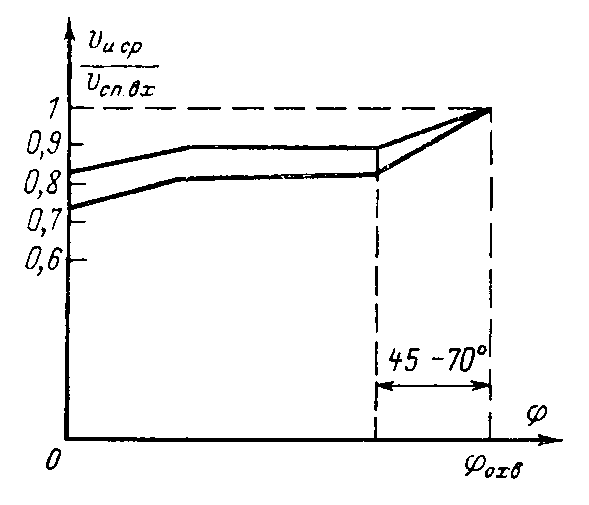 Рис. 13.8. Законы убывания средней скорости в спирали 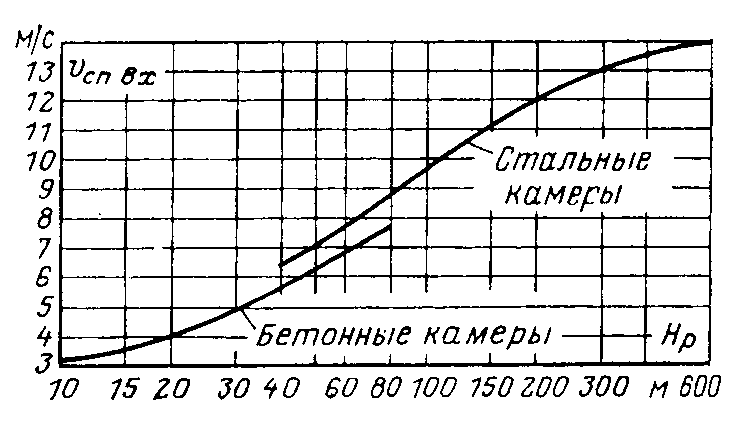 Рис. 13.9. Зависимость средней скорости во входном сечении спирали от напора Значение средней скорости во входном сечении vсп.сх желательно брать бóльшим, это приводит к уменьшению размеров спиральной камеры, но в то же время при чрезмерном увеличении vсп.сх заметно растут потери (снижается КПД) и сокращается пропускная способность турбины. Кривая vсп.сх = f(Нр), где Нр — расчетный напор турбины, показана на рис. 13.9. Расчет спирали по убывающей средней скорости (рис. 13.8) позволяет на 10-20% (бóльшие значения для бетонных камер) увеличить vсп.сх по сравнению с рис. 13.9 без ощутимого ухудшения энергетических показателей. Площадь меридианного сечения спиральной камеры:  , (13.2)причем в случае vu ср = const берут vu ср = vсп.сх. Габариты стальной спиральной камеры с круглыми поперечными сечениями определяются просто: задаются различными значениями углов и для каждого угла по (13.2) вычисляются площади и радиусы:  .Окружности сечений вписываются так, что они касаются верхнего и нижнего статорных поясов, как показано на рис. 13.7. Для бетонных камер сначала определяют угол охвата охв (рис. 13.4) и по (13.2), приняв = охв и vu ср = vсп.сх (рис. 13.9), вычисляют необходимую площадь входного сечения спирали Fсп.вх. По условиям компоновки блока здания ГЭС выбирается форма поперечного сечения (рис. 13.5) и строится входное сечение. При этом учитывают следующие условия: 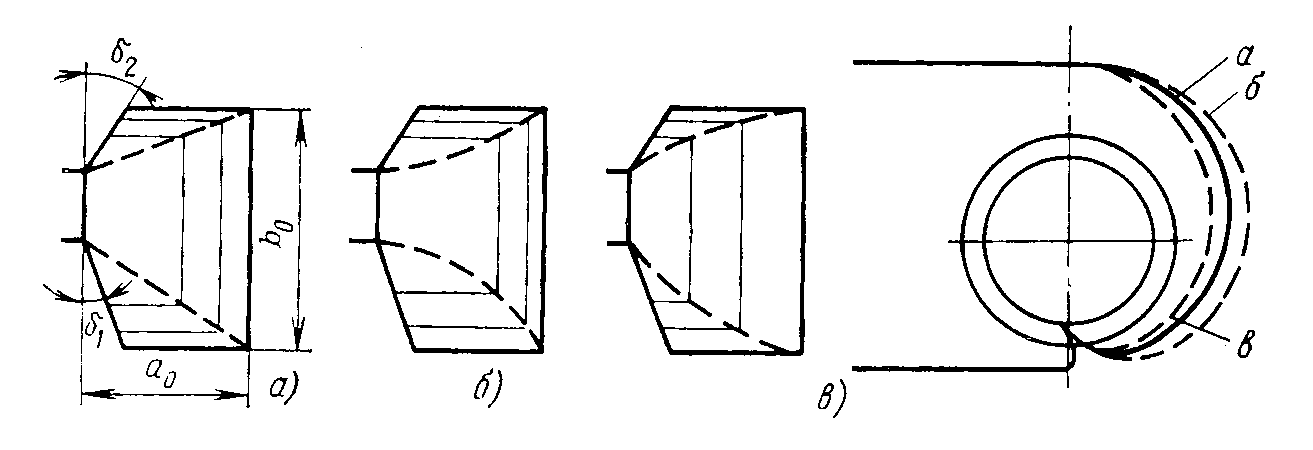 , углы 1 и 2 принимаются 15-30º (рис. 13.10). Способ построения промежуточных сечений задается кривыми пересечения вертикальной стенки с потолком и дном. Возможны три варианта (рис. 13.10): а — равномерное сокращение высоты и ширины; б — более быстрое сокращение высоты и в — более быстрое сокращение ширины. В плане форма в — самая обжатая, форма б — самая широкая. Рис. 13.10. Построение промежуточных сечений бетонных спиральных камер 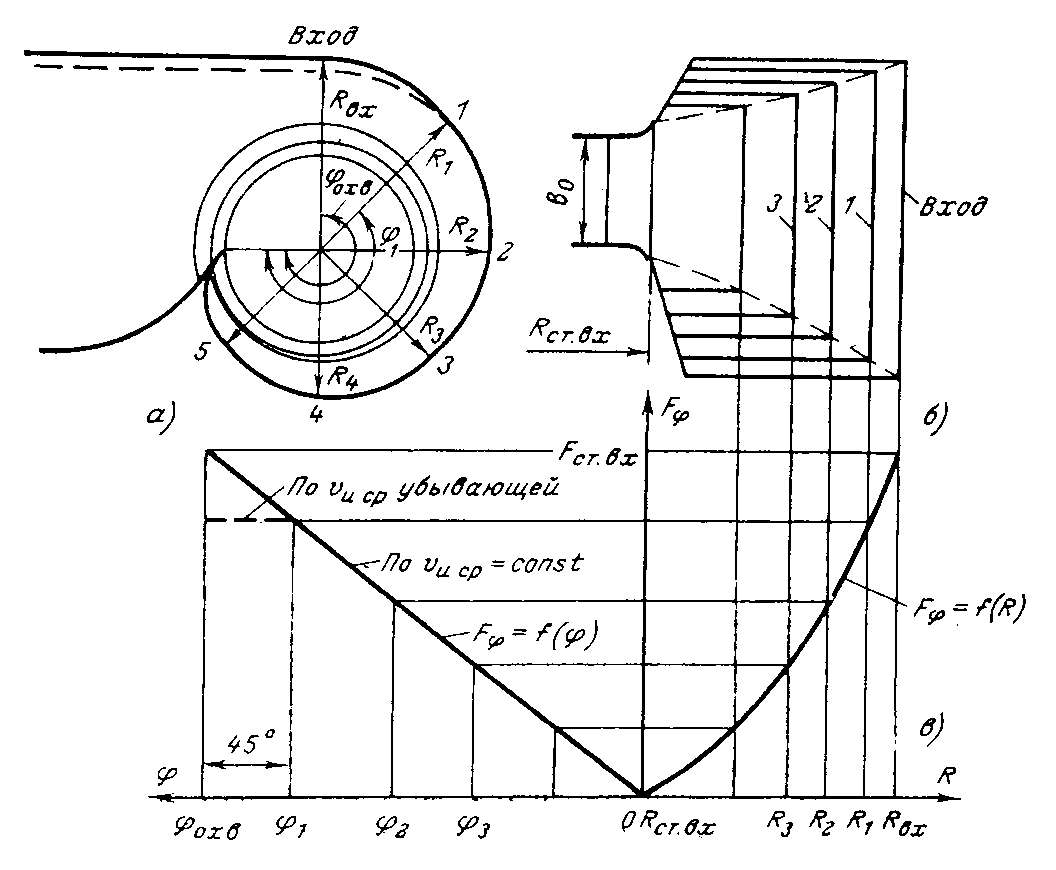 Рис. 13.11. Графическое определение размеров бетонной спиральной камеры Построение бетонной камеры удобно производить графическим способом, рис. 13.11. Задав охв (рис. 13.4) и найдя по (13.2) площадь  ,исходя из условий компоновки блока здания ГЭС выбирают форму и подбирают размеры входного сечения по площади Fсп.сх, по известным размерам статора (Rст.вх и b0) строят полученное сечение (вход на рис. 13.11, б) и, выбрав закон его изменения по длине (пунктирные линии), наносят несколько промежуточных сечений (1, 2, 3…). Под сечением строят сдвоенный график (рис. 13.11, в):  и  по (13.2). Снося промежуточные сечения на эти кривые, находят соответственные значения  … и 1, 2, …, которые позволяют построить спираль в плане (рис. 13.11, а).Если требуется уменьшить размер входного сечения, то можно использовать закон убывающей скорости на угле около 45º (показано пунктиром на рис. 13.11, а). Отсасывающая труба существенно влияет на энергетические показатели турбин, особенно низконапорных. Отсасывающая труба в значительной мере определяет размеры нижней части блока здания ГЭС и отметку заложения основания. Гидравлические показатели отсасывающих труб: средняя скорость v2 на входе в трубу (сечение 2-2 на рис. 13.12) зависит от режима работы турбины; абсолютное давление в сечении 2-2 при работе турбины ра2/g; ра5/g = h5 + ратм/g (h5 — заглубление сечения 5-5 под уровень нижнего бьефа); ратм — атмосферное давление. 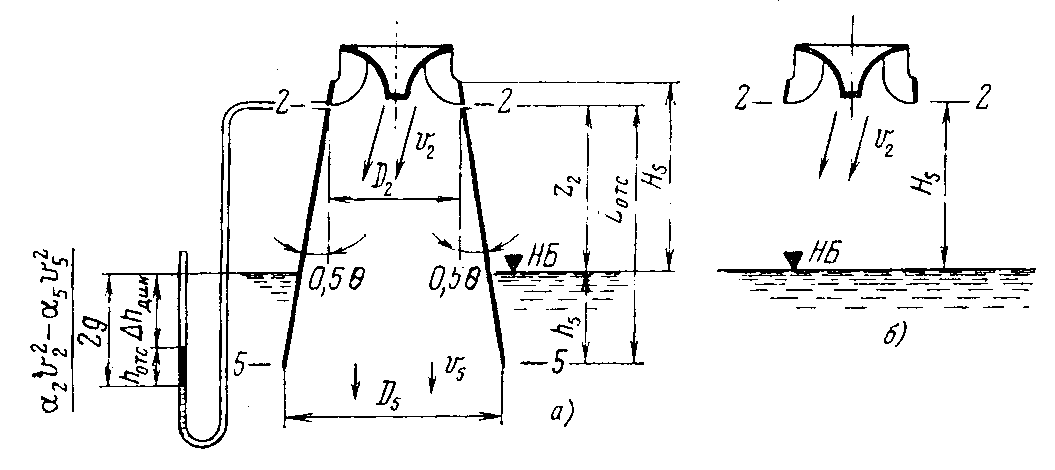 Рис. 13.12. Гидравлические показатели отсасывающих труб Высота установки турбины относительно нижнего бьефа, называемая высотой отсасывания Нs, отсчитывается от определенной плоскости турбины, можно принять z2 = Hs. Отсасывающая труба создает понижение давления (вакуум) под рабочим колесом, которое слагается из двух частей: из статического понижения давления Нs, которое не зависит от расхода, и динамического понижения давления  ,где hотс — гидравлические потери в отсасывающей трубе, определяемого диффузорным действием отсасывающей трубы и возрастающего с увеличением расхода. Энергетические показатели отсасывающей трубы. Энергия е2, с которой вода покидает рабочее колесо, не может быть использована турбиной и представляет собой потерю. Всегда стремятся снизить е2 и за счет этого увеличить КПД турбины. Это достигается отсасывающей трубой, представляющей собой плавно расширяющийся диффузор.  . (13.3)При наличии отсасывающей трубы теряемая энергия е2 состоит из выходных потерь  и внутренних потерь hотс.Для уменьшения теряемой энергии е2 можно увеличить площадь выходного отверстия трубы F5 (приводит к снижению v5), однако при этом потери hотс возрастают. Эти потери определяются трением о стенки, которое имеет малое значение, и вихревыми потерями, вызываемыми диффузорностью. Угол можно увеличить до 12-14º и даже более, не вызывая увеличения потерь, а даже получая некоторое их снижение. С этой целью поток за рабочим колесом должен быть не осевым, а иметь небольшую крутку, что достигается подбором соответственного режима (угол 2 0). Тогда возникающие центробежные силы препятствуют отрыву потока от стенок. Энергетический эффект отсасывающей трубы. Без отсасывающей трубы  . (13.4)Сравнивая (13.4) с (13.3), устанавливаем, что отсасывающая труба увеличивает используемую турбиной энергию на  . (13.5)Отсюда следует, что отсасывающая труба позволяет: 1) полностью использовать энергию, соответствующую высоте установки турбины Нs над нижним бьефом (важно только при Hs > 0); 2) использовать значительную часть кинетической энергии, которой обладает вода при выходе из рабочего колеса. Коэффициент полезного действия, или коэффициент восстановления отсасывающей трубы отс 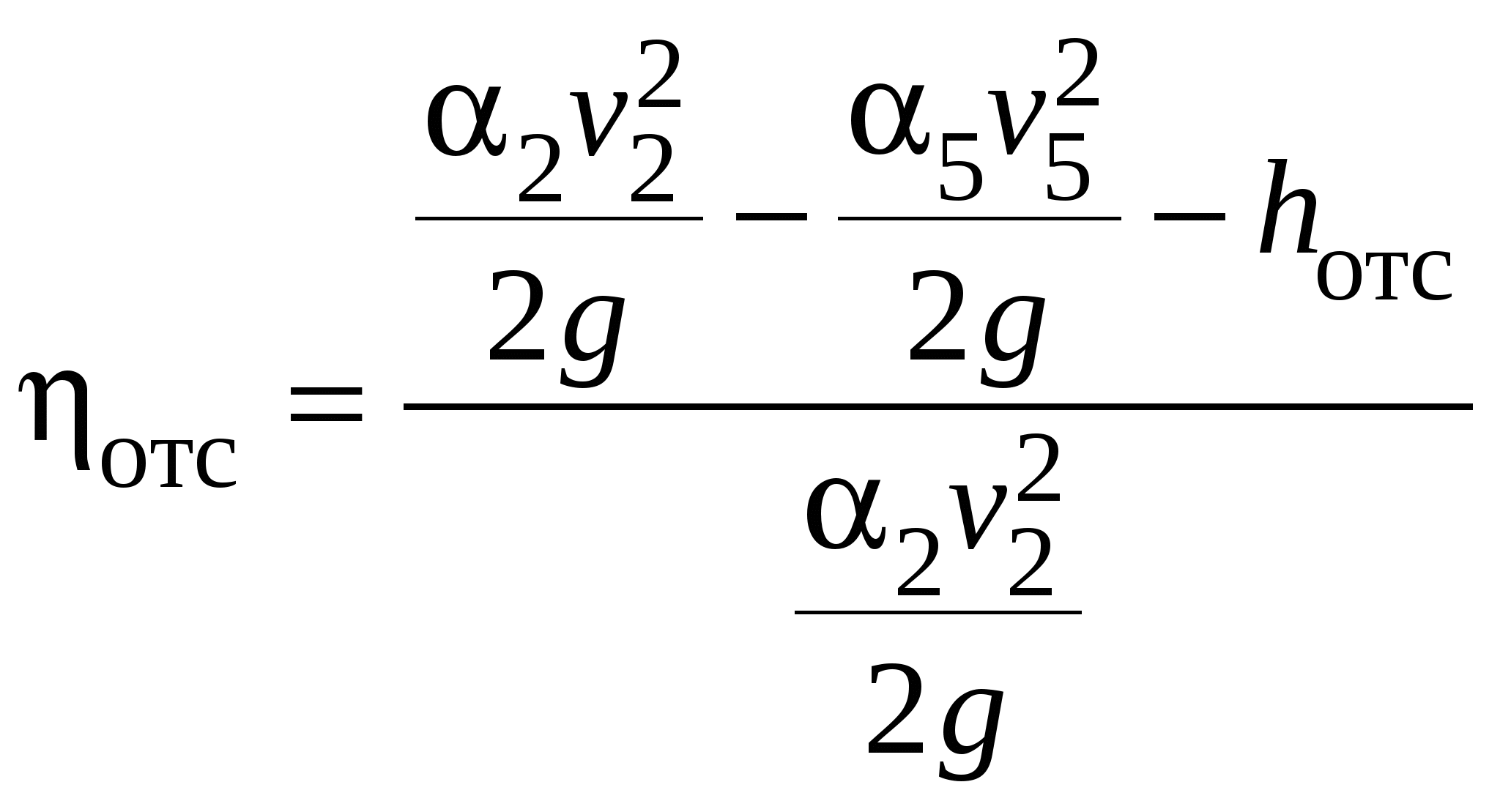 . (13.6)Для хороших отсасывающих труб отс достигает 80-85%. От всей энергии, располагаемой турбиной, кинетическая энергия потока за рабочим колесом составляет  . (13.7)Зависимость е2 кин/Н от напора для полной мощности турбин показана на рис. 13.13. В низконапорных турбинах кинетическая энергия за рабочим колесом может составлять 50-90% суммарной энергии Н и только у высоконапорных турбин при H > 100 м она составляет менее 10%. Возможность использования кинетической энергии е2 в значительной мере определяет эффективность турбин, указывает на большое значение отсасывающих труб, особенно при низких и средних напорах. 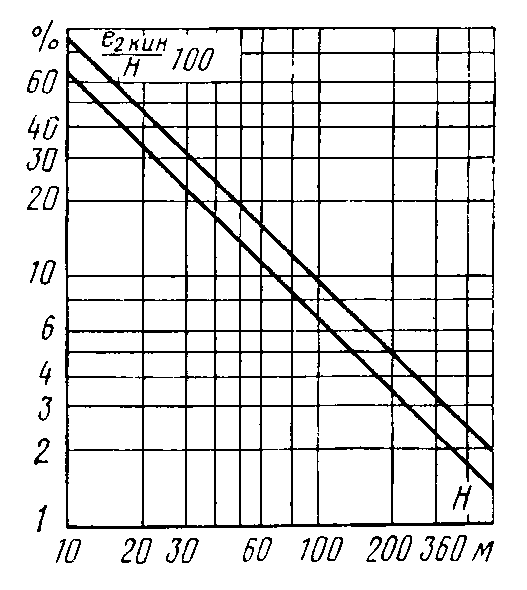 Рис. 13.13. Зависимость относительной кинетической энергии за рабочим колесом от напора турбины Отсасывающие трубы подразделяют на прямоосные и изогнутые. Прямоосные трубы применяются только для мелких турбин и для горизонтальных капсульных агрегатов (рис. 13.14, в). Изогнутые отсасывающие трубы используются практически на всех ГЭС с крупными вертикальными турбинами. Труба (рис. 13.15) состоит из трех основных частей: А — конуса; Б — колена и В — отводящего диффузора. В пределах конуса поперечные сечения трубы круглые, далее в колене они плавно переходят в прямоугольные с более быстрым увеличением ширины и в диффузорной части сохраняются прямоугольными, причем сечение нарастает за счет высоты (потолок имеет наклон под углом ). 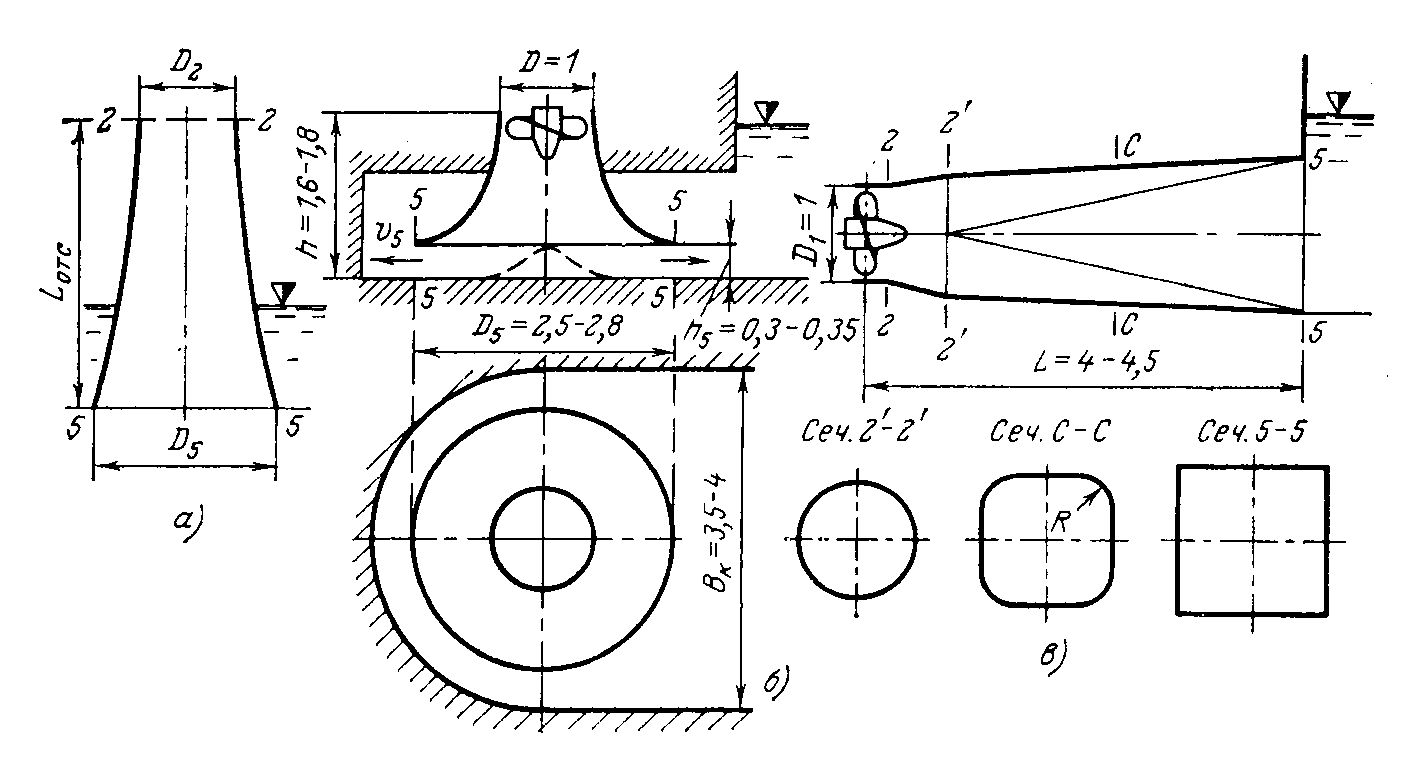 Рис. 13.14. Прямоосные отсасывающие трубы 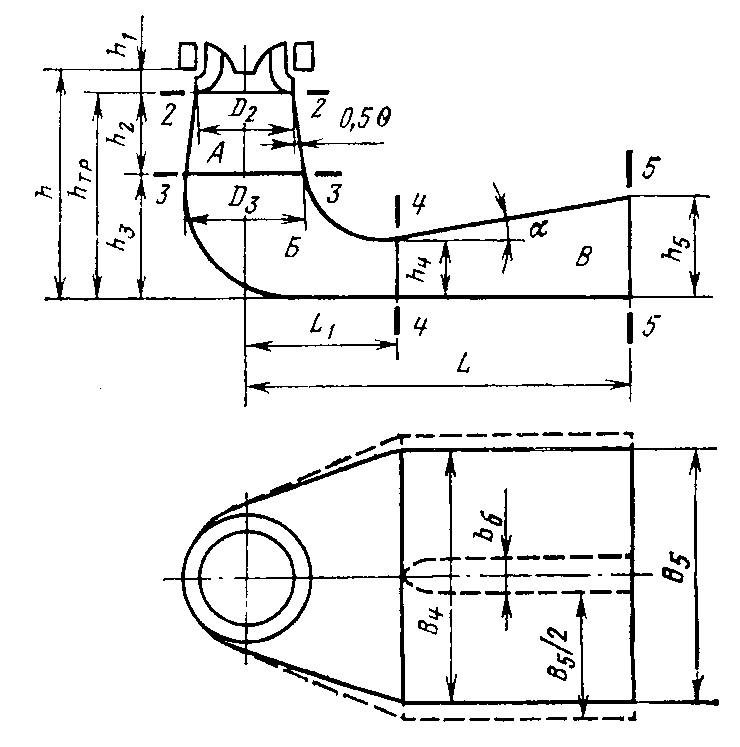 Рис. 13.15. Изогнутая отсасывающая труба Наиболее характерными размерами изогнутой отсасывающей трубы являются высота h, которая берется от низа направляющего аппарата (фактическая высота трубы hтр меньше и слагается из высоты конуса h2 и высоты колена h3), и длина трубы L (в действительности это длина горизонтальной части). В России используются изогнутые трубы с типовым коленом (рис. 13.16). Оно образовано из простых поверхностей: конической 1, цилиндрических 2 и 3, торовой 6, плоскостей 4, 5 и 7. Это упрощает изготовление опалубки. Колено может быть симметричным в плане или со смещением средней линии отводящего диффузора. Многие фирмы применяют плавно очерченные колена с криволинейными поперечными сечениями. По энергетическим показателям предпочтительнее более высокая труба. Но с ростом h увеличиваются объем работ и стоимость ГЭС. Поэтому высота трубы определяется технико-экономическими соображениями. Большинство ПЛ турбин имеют трубы высотой 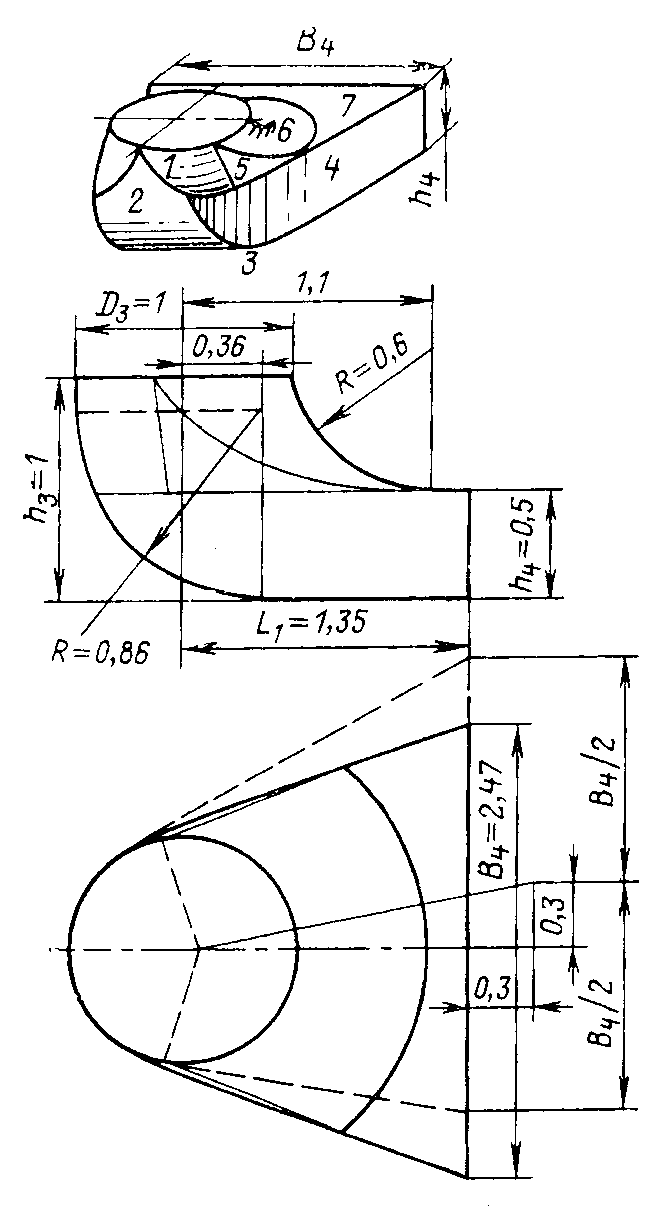 = 1,9 и 2,5. Для РО турбин применяют трубы высотой = 2,5÷3,0. Рис. 13.16. Типовое колено изогнутой отсасывающей трубы Ширина отсасывающей трубы В5 = В4 тем больше, чем больше . Так, для = 1,9 В5 = 2,2D1, а для = 2,7 В5 = 2,8D1. Если В5 превышает 10-12 м, то с целью облегчения фундаментной плиты ГЭС и уменьшения пролета затворов в диффузоре ставится один, а иногда два промежуточных бычка (см. рис. 13.15). При этом нужно обеспечить, чтобы суммарная ширина в свету В5 сохранилась.Используемые типы изогнутых отсасывающих труб показаны на рис. 13.17. Несимметричная отсасывающая труба (рис. 13.17, а) удобна по условиям компоновки блока здания ГЭС (пунктиром показан контур спиральной камеры). Часто с целью снижения объемов работ диффузор трубы делают наклонным (до 12º). При этом высота выходного сечения h5 сохраняется. 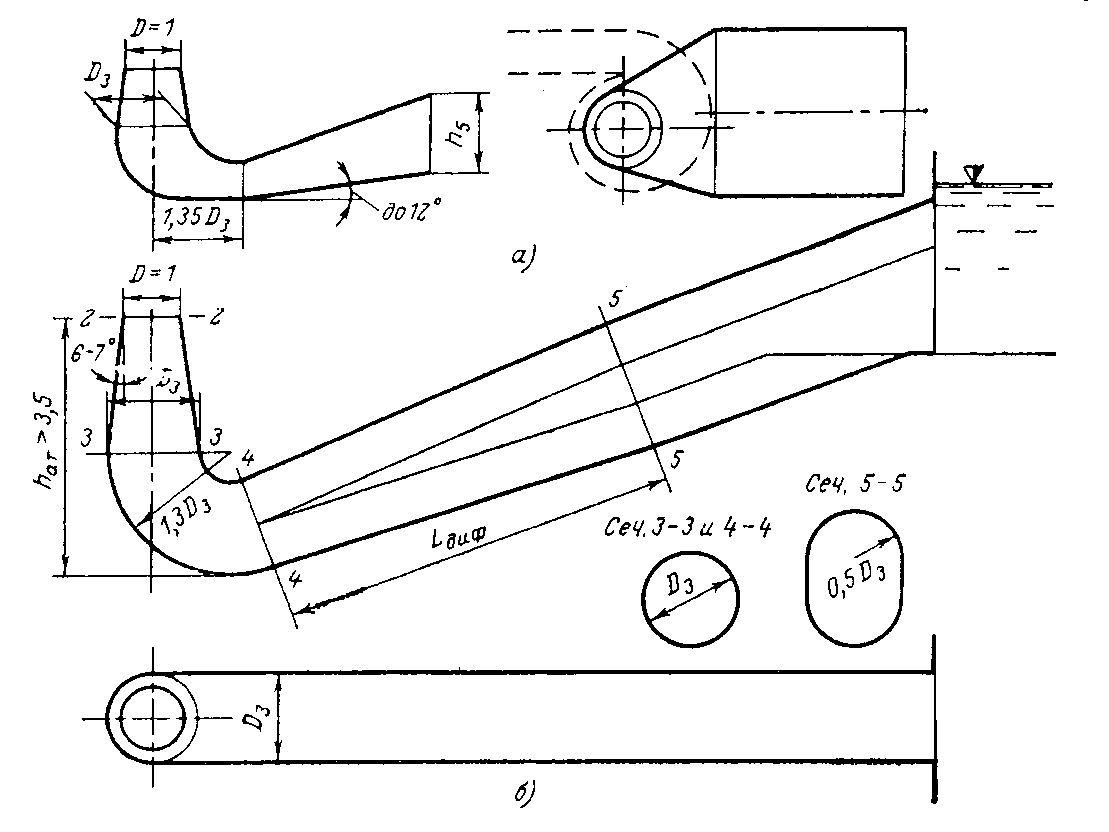 Рис. 13.17. Различные типы изогнутых отсасывающих труб В подземных и полуподземных ГЭС увеличение высоты трубы не приводит к ощутимому удорожанию, поэтому на этих станциях применяют трубы с > 3,5 (рис. 13.17, б), но стремятся ограничить ширину, чтобы имелась возможность сохранить целики скалы между выработками.Для горизонтальных мелких РО турбин применяется коленчатая отсасывающая труба (см. рис. 13.1, б). Под рабочим колесом турбины с отсасывающей трубой создается пониженное давление. Кроме того, при обтекании лопастей рабочего колеса на их тыльной стороне создается дополнительное снижение давления. Таким образом, в некоторой части проточного тракта гидромашины давление может быть весьма низким (глубокий вакуум). Эти условия могут приводить к возникновению кавитации. 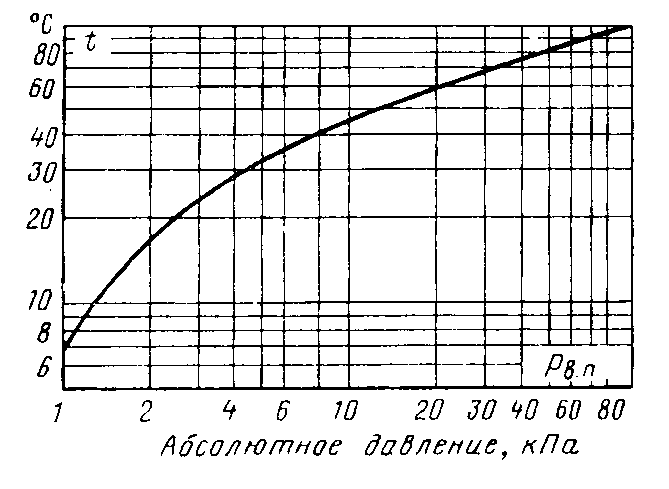 Рис. 13.18. Зависимость давления насыщенного водяного пара от температуры Когда давление в жидкости падает ниже давления насыщенного пара, начинается интенсивный переход жидкости в газообразное состояние — пар (кипение) и образуются местные разрывы сплошности — каверны, заполненные водяным паром. После образования каверн дальнейшее понижение давления в жидкости не происходит, так как оно компенсируется быстрым увеличением объема каверн. При повышении давления каверны захлопываются и пар мгновенно конденсируется. В турбулентном потоке мгновенное давление в точке определяется двумя компонентами:  ,где ра — осредненное во времени абсолютное давление; р′ — пульсационная компонента. В отдельные моменты времени ра.мгн будет достигать рв.п и здесь будут образовываться местные каверны, которые тотчас захлопнутся с повышением давления. С уменьшением ра число каверн возрастает, но они также будут возникать и захлопываться — пульсировать. Возникновение в турбулентном потоке разрывов сплошности жидкости — каверн, и их захлопывание с формированием в точках потока высокого динамического давления носит название кавитация. Кавитирующий поток вызывает воздействия на гидромашины: 1) при достаточно развитой кавитации возрастают гидравлические потери, что приводит к падению КПД и уменьшению расхода; 2) в гидромашине возникает резкий характерный шум и создаются повышенные вибрации; 3) довольно быстро в местах, где захлопываются каверны, образуется износ поверхности. Кавитационный износ (эрозия) вызывается главным образом механическим воздействием кавитирующего потока, которое проявляется в виде ударов высокой частоты, возникающих при захлопывании каверн на обтекаемой поверхности или вблизи нее. При этом проявляются усталостные явления в металлах. Разрушение происходит в форме выкрашивания, выбивания отдельных кристаллов, и поверхность металла вместо гладкой становится губчатой. Характерные виды кавитации (рис. 13.19): а — профильная, возникающая при обтекании лопастей в области наиболее низкого давления; б — щелевая при протекании жидкости с большим перепадом давления через зазоры, например между лопастями рабочего колеса и камерой, и в — местная, вызываемая обтеканием неровностей, отдельных уступов, ребер и др., например головок болтов. Кавитация, в основном профильная, имеет различные формы или стадии развития (рис. 13.20): а — пузырьковую форму кавитации, при которой разрывы сплошности имеют вид отдельных движущихся пузырьков; б — зональную или пленочную с наличием сплошной каверны, заполненной пульсирующими вихрями жидкости; в — отрывную с полостью, не заполненной жидкостью, и г — суперкавитацию, при которой полость настолько развита, что она замыкается за пределами обтекаемого профиля. Кавитация ухудшает энергетические и эксплуатационные показатели гидромашин, т. е. представляет собой опасное явление, недопустимое при нормальной эксплуатации. 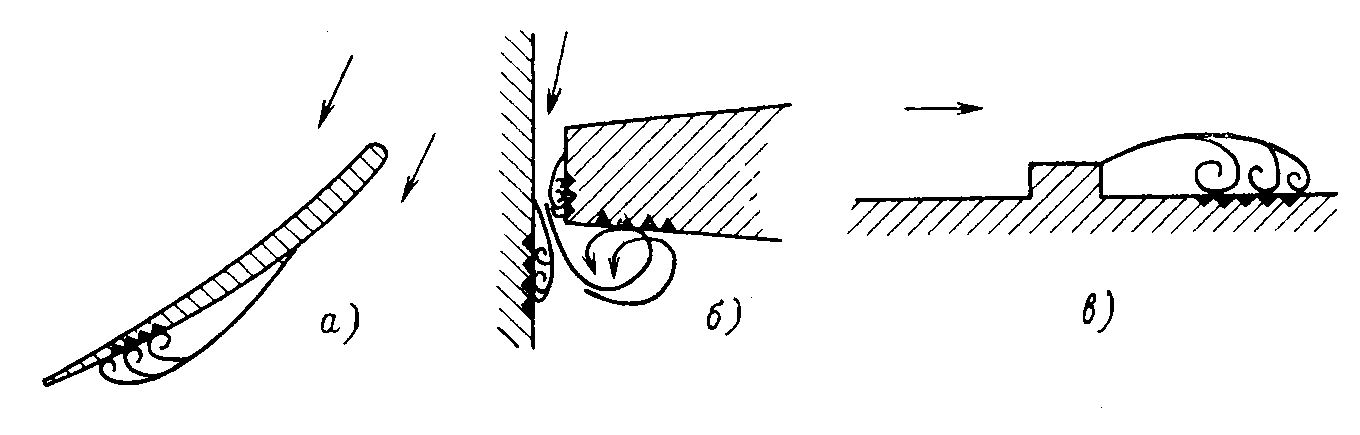 Рис. 13.19. Виды кавитации в гидромашинах 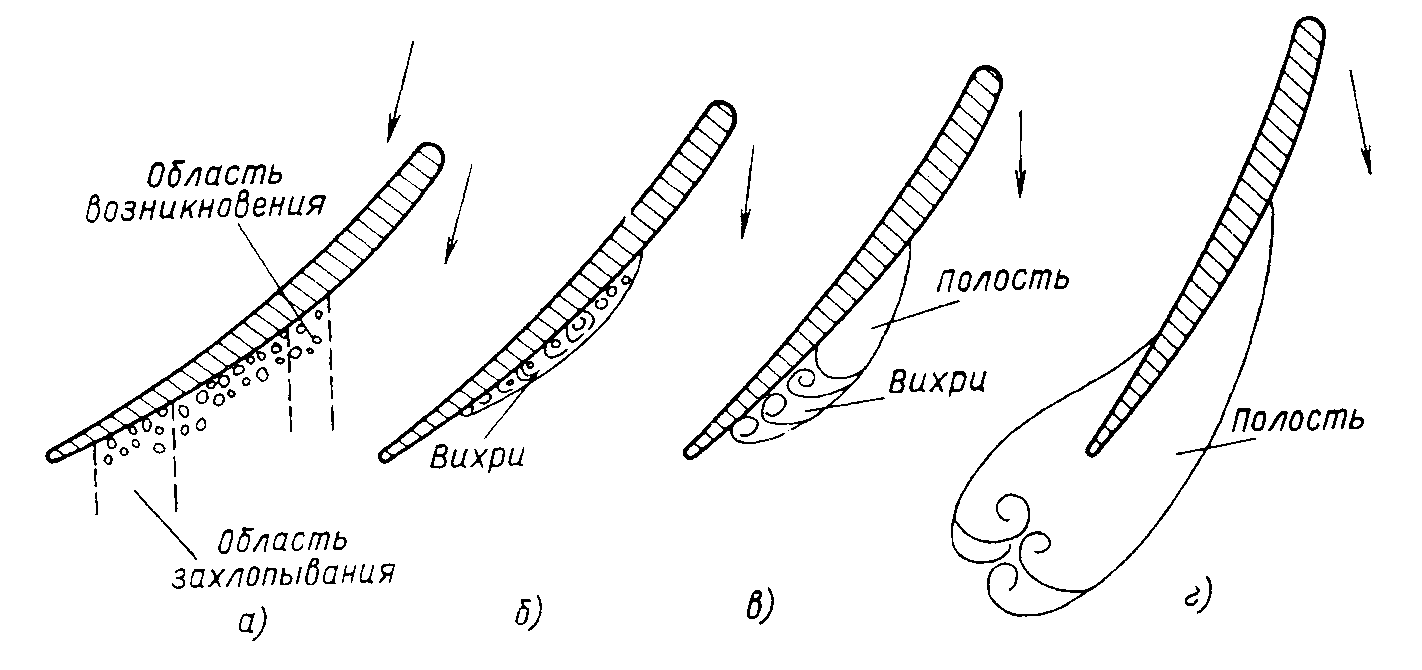 Рис. 13.20. Стадии (формы) лопастей кавитации Кавитация не будет возникать, если во всех точках проточного тракта давление ра i будет выше давления насыщенного водяного пара рв.п. Условие отсутствия кавитации записывается так:  . (13.8)Рассматривая баланс давлений в некоторой точке с в рабочем колесе, про которую известно, что в ней абсолютное давление ра с минимально, в итоге получим  . (13.9)Коэффициент есть коэффициент кавитации. Он показывает, какую часть напора турбины составляет динамическое разрежение в проточном тракте турбины (рис. 13.21) 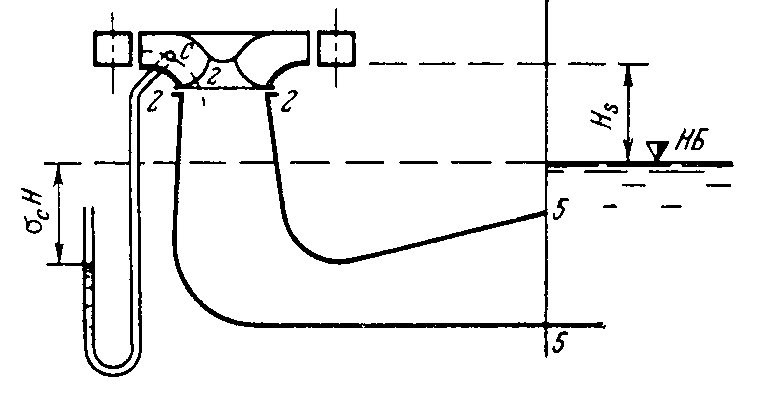 Рис. 13.21. К определению коэффициента кавитации Зная ра с, можем выразить условие отсутствия в турбине кавитации по (13.8):  . (13.10)Отсюда устанавливается значение высоты отсасывания:  . (13.11)Чтобы в турбине не возникала кавитация, необходимо ограничивать высоту отсасывания Нs. Для холодной воды можно принять рв.п /g = 0,3 м (рис. 13.18). В этих условиях  . (13.12)Здесь т — расчетный коэффициент кавитации турбины;  — абсолютная отметка нижнего бьефа.Значения коэффициента кавитации определяются экспериментальным путем на специальном кавитационном стенде. Они соответствуют моменту возникновения кавитации и называются критическими. При расчетах допустимой высоты отсасывания Нs расчетный коэффициент кавитации турбины т определяют по критическому значению с введением коэффициента запаса k, который принимается равным 1,1-1,2:  .Значения берутся с характеристик турбин. Обобщенная зависимость = f (ns ном) для условий номинальной (максимальной) мощности турбин по опытным данным показана на рис. 13.22, причем указан диапазон возможных отклонений для различных типов турбин. С ростом быстроходности турбины коэффициент кавитации быстро увеличивается. 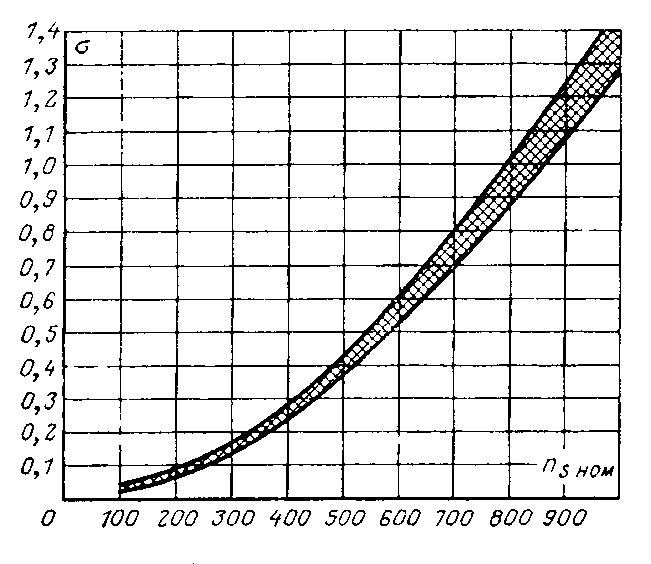 Рис. 13.22. Зависимость коэффициента кавитации от быстроходности при номинальной (максимальной) нагрузке Способы отсчета высоты отсасывания Нs, определяемой по (13.12) — расчетной, для различных турбин показаны на рис. 13.23. В вертикальных РО и диагональных турбинах Нs отсчитывается от нижней кромки направляющего аппарата; в вертикальных осевых турбинах — от оси поворота лопастей рабочего колеса; в горизонтальных турбинах — от верхней точки рабочего колеса. 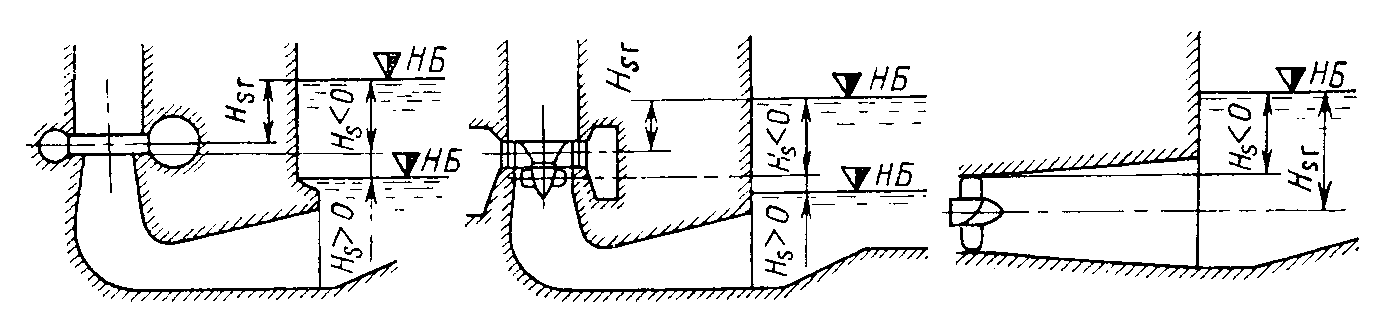 Рис. 13.23. Отсчет высоты отсасывания Нs в различных турбинах |