Конспект лекций по дисциплине силовая электроника по направлению 140400. 62
 Скачать 1.41 Mb.
|
Сглаживающие фильтры постоянного напряженияКомплексный коэффициент передачиПри анализе сложных электрических цепей, в частности фильтров, которые могут быть представлены в виде четырехполюсника, то есть имеют вход и выход, удобно использовать комплексный коэффициент передачи  .Где  и  могут быть различными, физически не однородными. При этом комплексный коэффициент передачи учитывает изменение модуля  и фазы  выходной переменной.Зная комплексный коэффициент передачи легко найти выходную переменную по известной входной переменной  .Если фаза выходной переменной не имеет значения, то достаточно знать модуль комплексного коэффициента передачи .Анализ сложных фильтровЕсли входной ток фильтра непрерывен, то при известном коэффициенте пульсаций на входе фильтра qВХ, зная модуль коэффициента передачи фильтра можно найти коэффициент пульсаций на выходе фильтра qВЫХ. Принято характеризовать фильтрующие свойства фильтра коэффициентом сглаживания или фильтрации  .Коэффициент пульсаций входного напряжения равен  ,где UmmВХ – амплитуда низшей гармоники пульсаций входного напряжения, UdВХ – среднее значение входного напряжения фильтра. Коэффициент пульсаций выходного напряжения равен  ,где UmmВЫХ – амплитуда низшей гармоники пульсаций входного напряжения, UdВЫХ – среднее значение входного напряжения фильтра. Коэффициент фильтрации соответственно равен  ,где  - коэффициент передачи постоянной составляющей напряжения, - модуль коэффициента передачи низшей гармоники пульсаций с частотой  .Пример. Схема Г-образного фильтра приведена на рис. 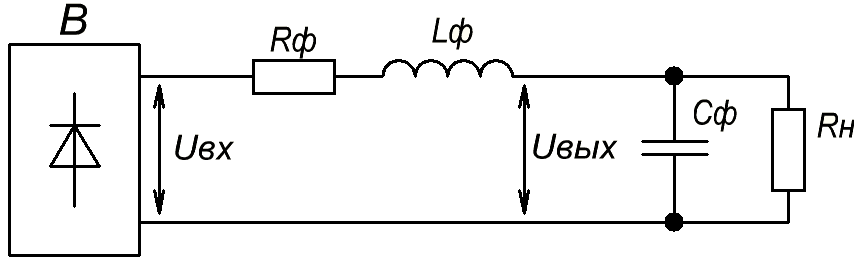  Рис. Источник питания с Г - образным LC - фильтром Обозначим за комплексные сопротивления:  ,  , тогда  . .Передача фильтра по постоянному току  .Коэффициент фильтрации соответственно равен  .Примерная зависимость коэффициента фильтрации от относительной 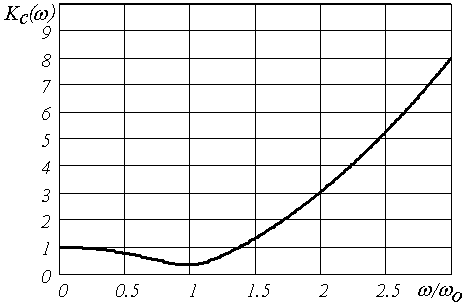частоты пульсаций  приведена на рис. Рис. Зависимость коэффициента фильтрации от относительной частоты пульсаций .За базовую частоту принята резонансная частота  .Резонансная частота выбирается значительно меньше частоты пульсаций, при этом коэффициент сглаживания приближенно определяется выражением  Анализ емкостного фильтраПростейшим фильтром, широко применяемым в маломощных выпрямителях, является емкостной фильтр. Принципиальные схемы двухфазных нулевой и мостовой схем выпрямления с емкостным фильтром приведена на рис. .  Рис. Двухфазные схемы выпрямления с емкостным фильтром: а) – нулевая; б) – мостовая схемы выпрямления Фильтр состоит из емкости СФ, которая включена на выходе выпрямителя параллельно нагрузке. Емкостной фильтр искажает выходное напряжение выпрямителя и не имеет раздельных входа и выхода, поэтому понятие комплексного коэффициента передачи не применимо. Точный анализ такого простейшего фильтра весьма сложен, поэтому ограничимся приближенным анализом, разбив задачу на две части: определение среднего выходного напряжения фильтра и определение его гармонического состава. Определение среднего выходного напряжения фильтра Для определения среднего выходного напряжения примем следующие допущения: напряжение фильтра (нагрузки) абсолютно сглажено; ток выпрямителя состоит из участков синусоид, то есть учитывается только активное сопротивление обмоток трансформатора, которое у маломощных трансформаторов значительно больше индуктивного. Диаграммы напряжений и тока выпрямителя при указанных допущениях приведены на рис. В диапазоне углов  ток выпрямителя равен ,где: RФ – фазное сопротивление трансформатора и проводов; 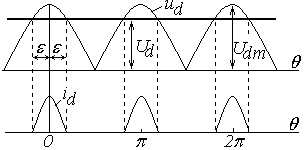 - угол отсечки. Рис. Диаграммы напряжений и тока при определении среднего выходного напряжения выпрямителя Средний ток нагрузки равен  Средний ток выпрямителя  ,где m – фазность схемы выпрямления. Решим совместно уравнения  .Обе части уравнения разделим на  , получим , применим разложение  , , разрешим уравнение относительно  .Знание угла отсечки позволяет найти среднее напряжение на нагрузке, средний выходной ток выпрямителя, средний ток диодов и, соответственно, рассчитать выпрямитель.Определение гармонического состава выходного напряжения фильтраПульсации выходного напряжения определим, считая, что  . С учетом этого условия заряд идет очень быстро, а разряд медленно с постоянной времени ТР = RHCФ. Примерный вид напряжения приведен на рис. , где m – фазность схемы выпрямления, f – частота сети. Рис. Форма напряжения на нагрузке при определении его гармонического состава В интервале повторяемости напряжение на нагрузке изменяется согласно уравнению  .Считая заряд емкости мгновенным, определим скачок напряжения при заряде емкости  Разложим напряжение на нагрузке как треугольную функцию в ряд Фурье и получим уравнение для амплитуд гармоник  , где m – фазность схемы выпрямления, а n – ряд натуральных чисел .При определении коэффициента пульсаций напряжения учитывается только низшая гармоника, соответственно он равен  .При заданном коэффициенте пульсаций можно найти емкость фильтра  .Сглаживающие фильтры переменного напряженияПо принципу фильтрации различают две группы фильтров: Фильтры основной гармоники, настроены на пропускание основной гармоники и задержку высших гармоник. Фильтры высших гармоник, настроенные в резонанс на высших гармониках. Фильтры основной гармоники В общем случае структура фильтра основной гармоники имеет вид  Напряжение на нагрузке  Коэффициент ослабления фильтра  Нерезонансный фильтр 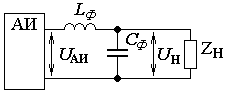  ,  , соответственно ,Введем понятия добротности реактора  и добротности конденсатора  , тогда  .При k>>1 модуль Кф примерно равен  .Фильтр хорошо фильтрует высшие гармоники, но ослабляет так же и основную гармонику. |