Начертательная геометрия. Конспект лекций по курсу нгииг л. В. Белозерцева, А. Г. Коробова, М. Н. Потапова

• Название: Конспект лекций по курсу нгииг л. В. Белозерцева, А. Г. Коробова, М. Н. Потапова
• Анкор: Начертательная геометрия
• Дата: 29.03.2023
• Размер: 1.12 Mb.
• Имя файла: 310.doc
• Тип: Конспект лекций; #1024690
• страница: 3 из 4

4.2. Следы плоскости

Прямую, по которой плоскость пересекает плоскость проекций, называют следом плоскости(рис.4.1.).

При этом различают:

- горизонтальный след - прямая, по которой плоскость пересекает горизонтальную плоскость проекций H (_н);

- фронтальный след - прямая, по которой плоскость пересекает фронтальную плоскость проекций V(_v);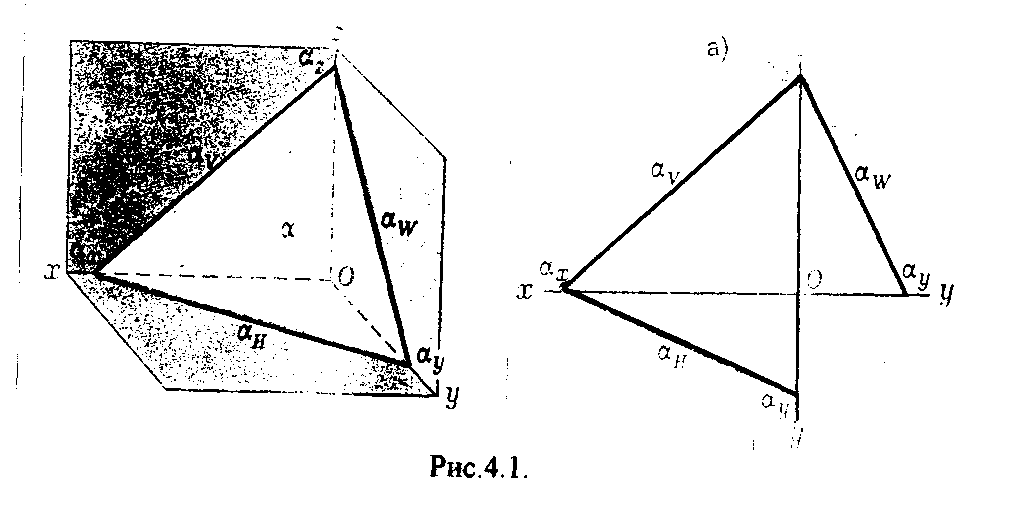

- профильный след - прямая, по которой плоскость пересекает профильную плоскость проекций W(_w).

Т
Рис.4.1.
очки в которых пересекаются (сходятся) два следа называются точками схода следов.

Для того, чтобы построить следы плоскости, надо найти следы двух произвольных прямых, принадлежащих этой плоскости.

Плоскость, не параллельную и не перпендикулярную ни к одной из плоскостей проекций, называют плоскостью общего положения.

4.3 Плоскости частного положения

Плоскости, параллельные или перпендикулярные какой либо плоскости проекции, называются плоскостями частного положения.

4.3.1. Проецирующие плоскости

Плоскости, перпендикулярные к плоскостям проекций, называются проецирующими (рис.4.2.).

Плоскость, перпендикулярная горизонтальной плоскости проекций называется горизонтально - проецирующей (рис.4.2.а.).

Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально - проецирующей (рис.4.2.6.).

Плоскость, перпендикулярная профильной плоскости проекций, называется профильно - проецирующей(рис.4.2.в.).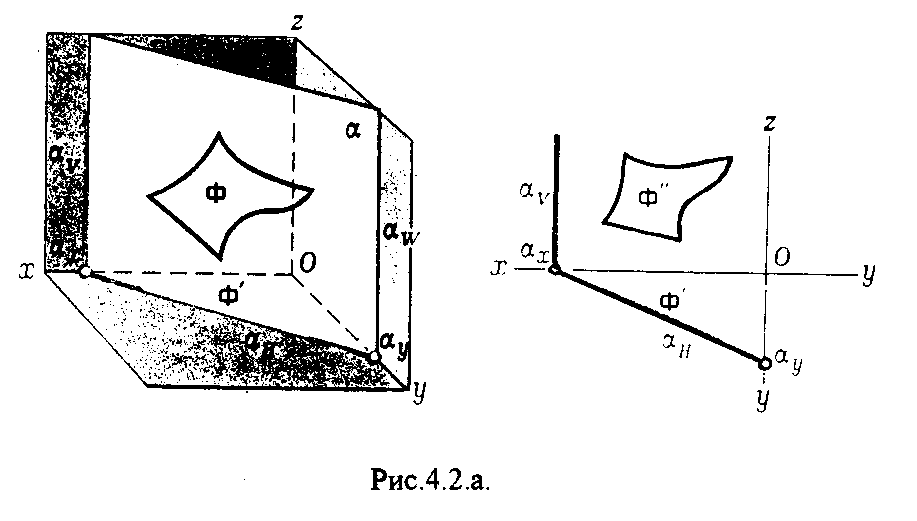






4.3.2. Плоскости уровня

Плоскости, перпендикулярные двум плоскостям проекций, называются плоскостями уровня.

Плоскости уровня параллельны какой-либо плоскости проекций:

- плоскость  -фронтальная плоскость (рис.4.3.а.);

- плоскость  -фронтальная плоскость (рис.4.3.б.);

- плоскость  - профильная плоскость (рис.4.3.в.).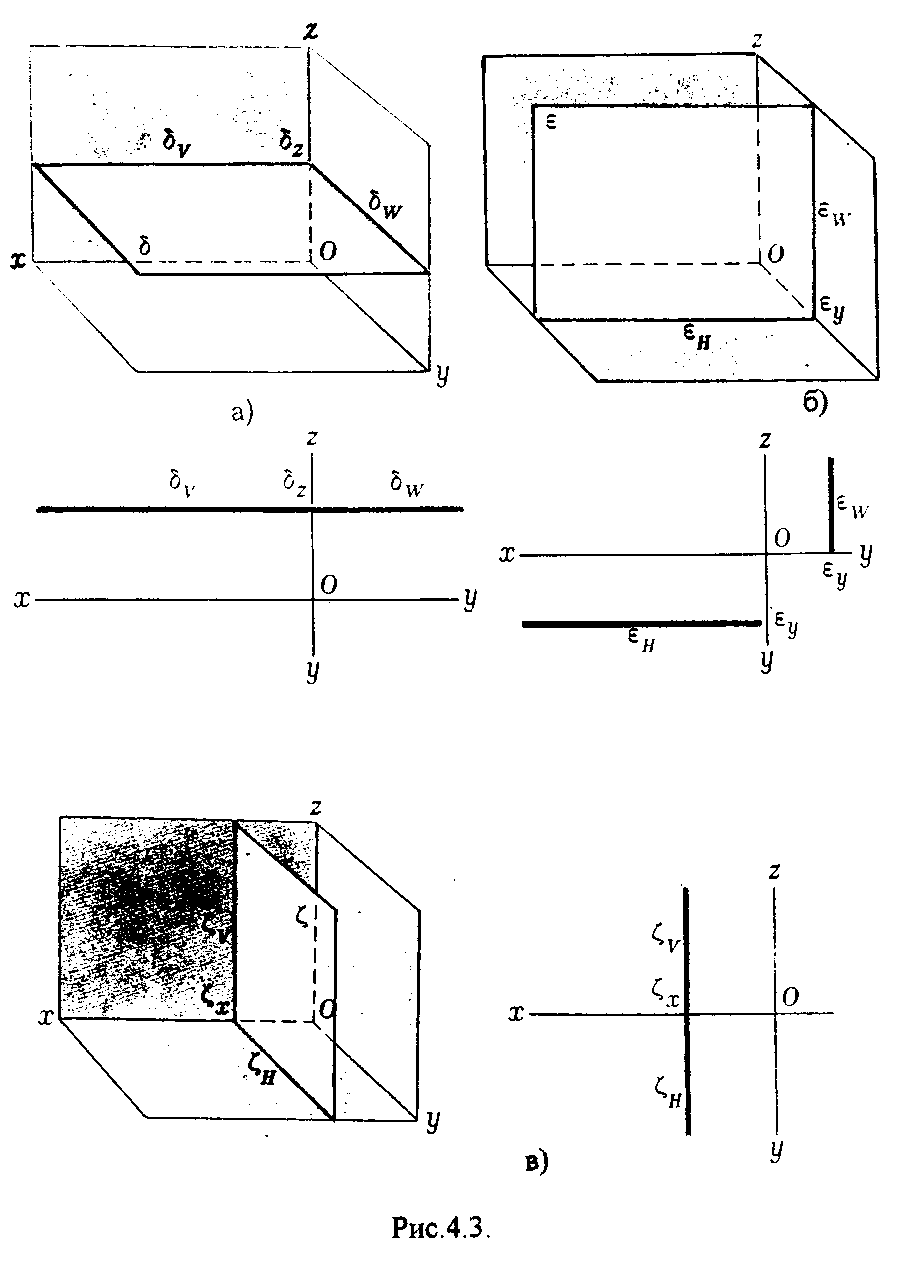

4.4. Линии уровня плоскости

Прямые, параллельные какой - либо плоскости проекции и принадлежащие заданной плоскости, называются линиями уровня плоскости.

Горизонталь плоскости - прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций (рис.4.4,а.).

Фронталь плоскости - прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций (рис.4.4.6.).

Профильнаяпрямая плоскости - прямая, принадлежащая плоскости и параллельная профильной плоскости проекций (рис.4.4,в.).

Следы плоскости также являются ее линиями уровня. Поскольку они лежат в плоскостях проекций, их еще называют нулевыми. Например, горизонтальный след - нулевая горизонталь и т.д.

У плоскостей, заданных следами, горизонтальная проекция горизонтали параллельна горизонтальному следу, фронтальная проекция фронтали параллельна фронтальному следу. профильная проекция профильной прямой параллельна профильному следу.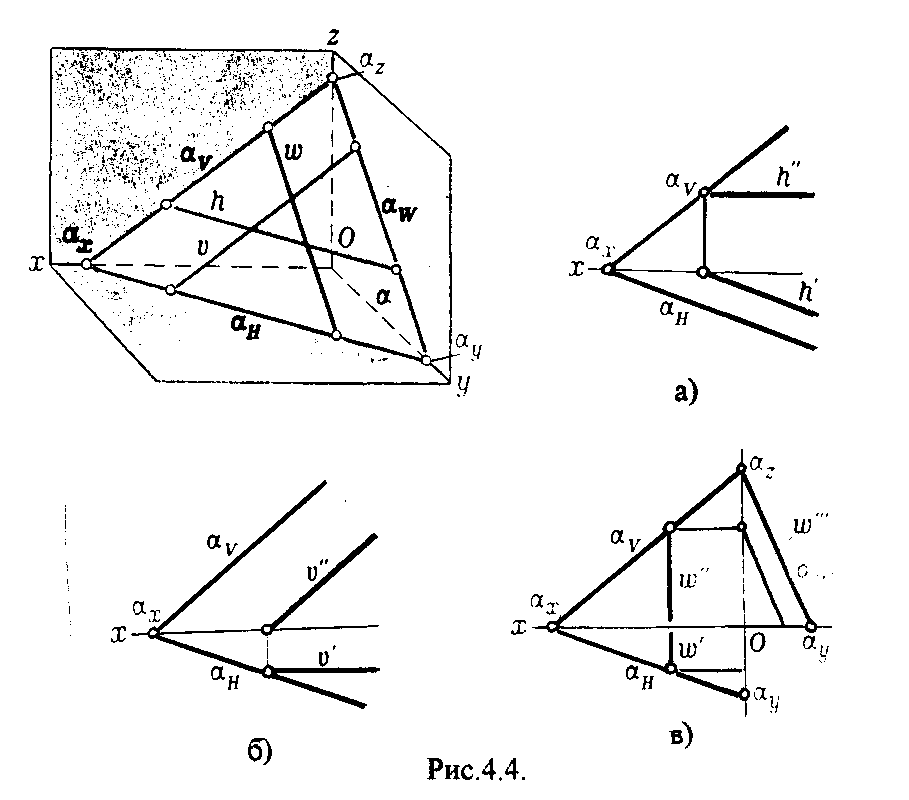



5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ,

ДВУХ ПЛОСКОСТЕЙ

Плоскости и прямые в пространстве могут быть взаимно параллельны либо пересекаться.

5.1. Построение линии пересечения двух плоскостей

Две плоскости пересекаются по прямой линии, следовательно, в общем случае для построения линии пересечения двух плоскостей достаточно найти две точки, принадлежащие одновременно каждой из заданных плоскостей.

Н 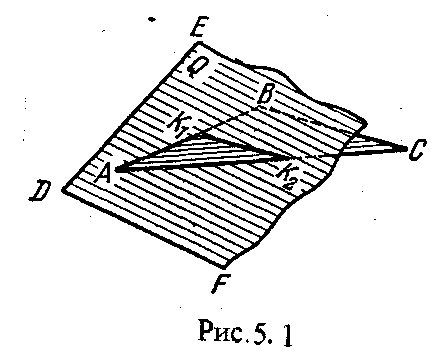а рис.5.1. такими точками являются К₁, К₂,







Выбор решения данной задачи зависит от расположения заданных плоскостей относительно плоскостей проекций.

Рассмотрим случай, когда хотя бы одна из пересекающихся плоскостей проецирующая. Рис.5.2, 5.3.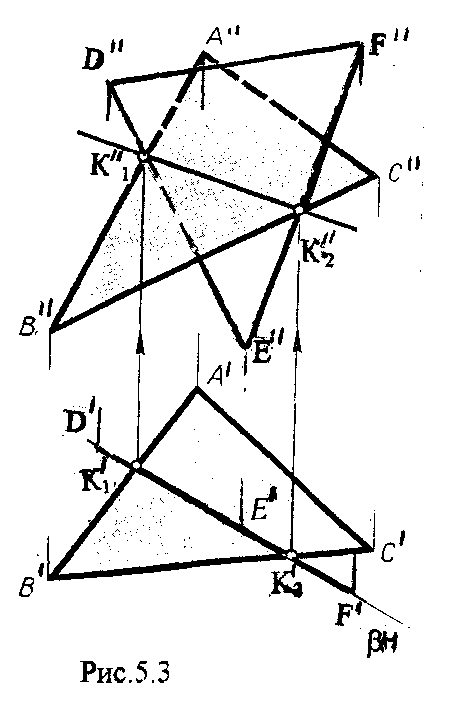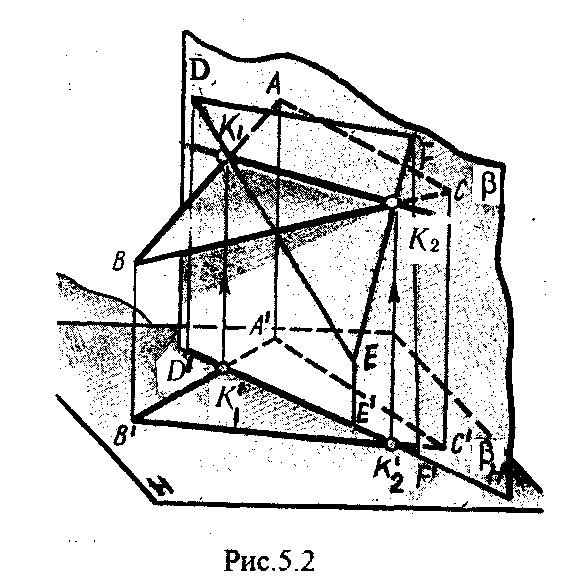





Даны плоскости (АВС) и (DEF), Плоскость  перпендикулярна к горизонтальной плоскости проекций, Так как треугольник DEF проецируется на плоскость Н в виде прямой линии (DF), то горизонтальная проекция l линии пересечения плоскостей  и  совпадает с DF, Обозначаем на этой проекции K₁ и K₂, затем определяем K₁ и K₂ по условию их принадлежности к сторонам треугольника ABC K₁AB, К₂ВС/

Рассмотрим общий случай построения линии пересечения двух плоскостей.

Способ построения линии пересечения двух плоскостей состоит в следующем (рис,5.4)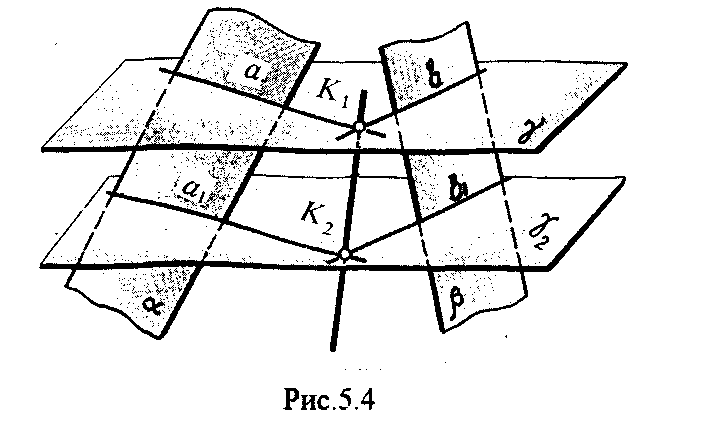



Заданные плоскости  и  пересекают третьей вспомогательной плоскостью . Находим линии пересечения плоскости  с плоскостью  и плоскостью 

а=    ; b=   .

Точка k₁ определяется в пересечении а и b. Для того, чтобы найти точку К₂, проведем описанные построения еще раз с еще одной вспомогательной секущей плоскостью.

Рассмотрим как этот алгоритм реализуется на чертеже (рис.5.5.). Плоскость  задана двумя пересекающимися прямыми (АВ, ВС).

Плоскость  задана параллельными прямыми (ED, GF). Обе плоскости общего положения.

Проведем вспомогательную секущую плоскость ₁ перпендикулярную V и пересекающую каждую из плоскостей  и .

При пересечении плоскости ₁ с плоскостью  получаем прямую «a₁» с проекциями 12, 12, а при пересечении ₁ с  получаем прямую «b₁» с проекциями 34, 34, Эти прямые расположенные в плоскости ₁ в своем пересечении определяют точку k₁ линии пересечения  и .

K₁= 1234 K₁ ₁

Введя затем плоскость ₂ получим:

a₂ = ₂ с проекциями 56, 56

b₂= ₂ с проекциями 78, 78

К₂= a₂Ь₂

К₂=5678

К₂ ₂

Затем определяем проекции искомой линии пересечения K₁K₂ и K₁K₂.

Е 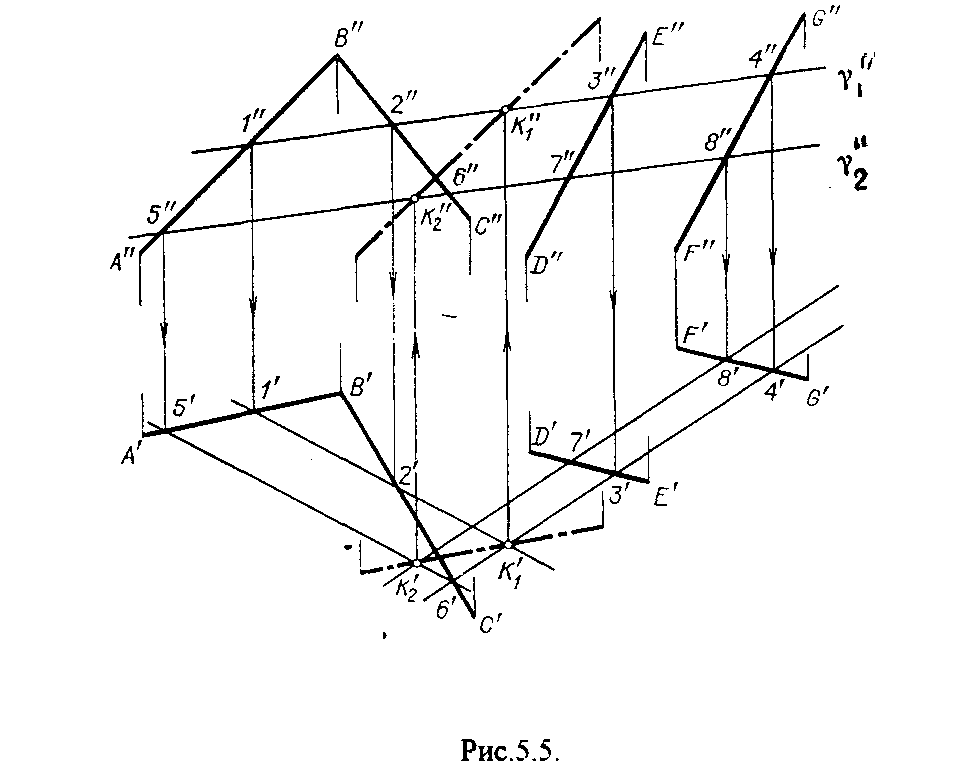сли плоскости заданы их следами на плоскостях проекций, то точки, определяющую прямую пересечения плоскостей, находят на пересечение одноименных следов плоскостей.

L₁=_H  _H; L₁=_V  _V

В этом случае плоскости проекции выполняют роль вспомогательных секущих плоскостей, а соответствующие следы несут функции проекций прямых а, b и а, b. (рис,5,6.).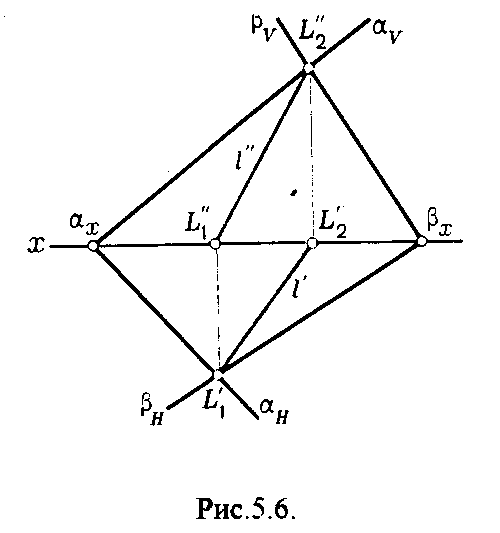


На рис.5.7. показан случай когда известно направление линии пересечения. Поэтому достаточно иметь лишь одну точку от пересечения следов и далее провести через эту точку прямую, исходя из положения плоскостей и их следов.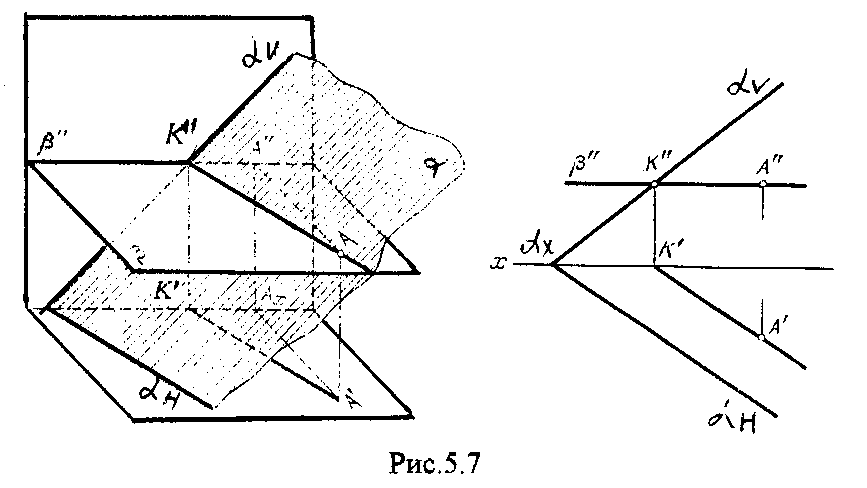




5.2. Пересечение прямой линии с плоскостью

Рассмотрим способы построения точки пересечения прямой с плоскостью при различном их расположении относительно плоскостей проекций.

1) Пересечение прямой линии с плоскостью перпендикулярной

к одной или двум плоскостям проекций.

Плоскость, перпендикулярная к плоскости проекций, проецируется на нее в виде прямой линии. На этой прямой должна находиться соответствующая проекция точки, в которой прямая пересекает плоскость.

На рис,5,8 фронтальная проекция К точки пересечения прямой АВ с плоскостью (CDE) определяется в пересечении проекций АВ и СЕ, т.к. пл.  проецируется на пл. V в виде прямой линии. Определить проекцию К, находим К по условию принадлежности на АВ.

Т.к. прямая АВ в направлении от К к В находится под треугольником, часть ее горизонтальной проекции является невидимой и потому проведена штриховой линией.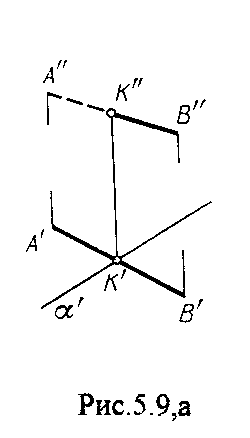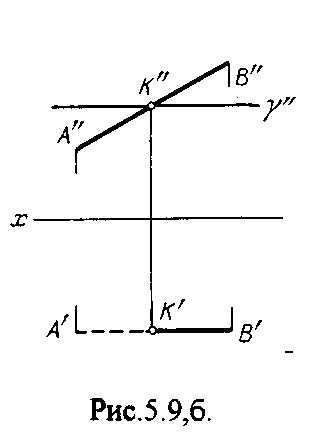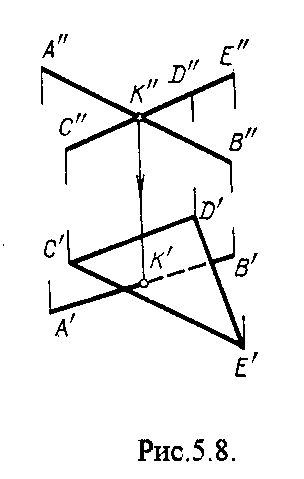




На рис.5.9а фронтальный след плоскости  является ее фронтальной проекцией. Проекция К определяется в пересечении проекции АВ и следа  . Аналогично решается задача на рис.5.9.б.

2) Пересечение проецирующей прямой с плоскостью

общего положения.

Прямая, перпендикулярная плоскости проекций проецируется на эту плоскость в точку. В эту же точку спроецируется искомая точка пересечения рис.5.10.

П 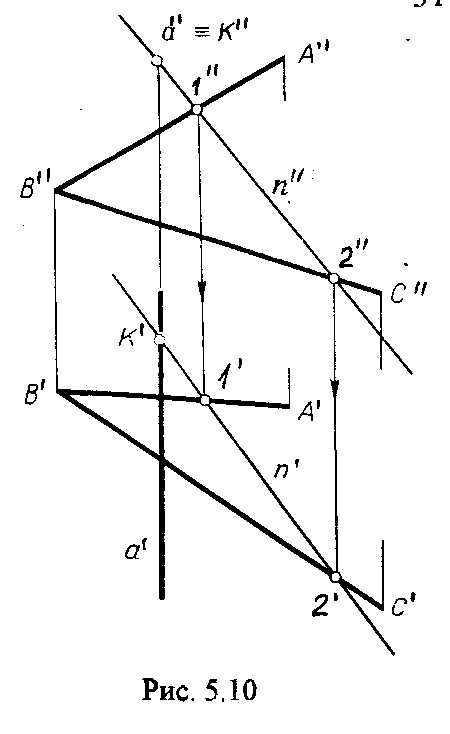рямая а  V, К сов-падает с а. Горизонтальную проекцию k₁ определяем по условию принадлежности точки к плоскости (АВС) точка К принадлежит плос-кости , т.к. она принадлежит прямой n₁ принадлежащей .

3) Пересечение прямой общего положения с плос-костью общего положения.

Построение точки пересе-чения произвольной прямой с плоскостью общего положения выполняют по следующему алгоритму (рис.5.11.).

1) Через данную прямую 1 проводится вспомогательная секущая плоскость ()

2) Определяется прямая (m) пересечения заданной плоскости () и вспомо-гательной ().

3) Находится точка К в пересечении прямых – данной 1 и построенной (m).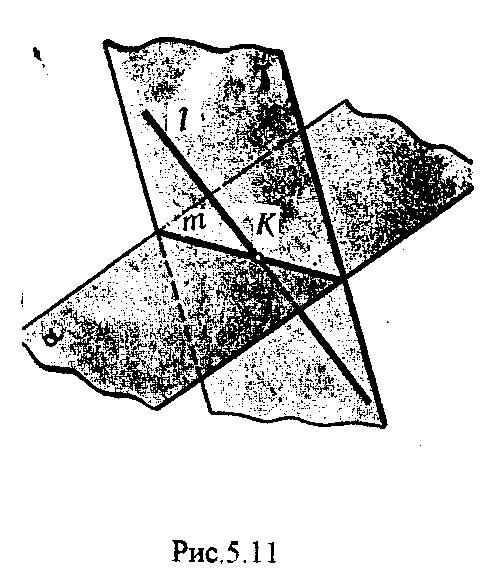




Рис.5.11.

На рис.5.12 и 5.13. показано построение точки пересечения прямой 1 с плоскостью общего положения , заданной треугольником ABC.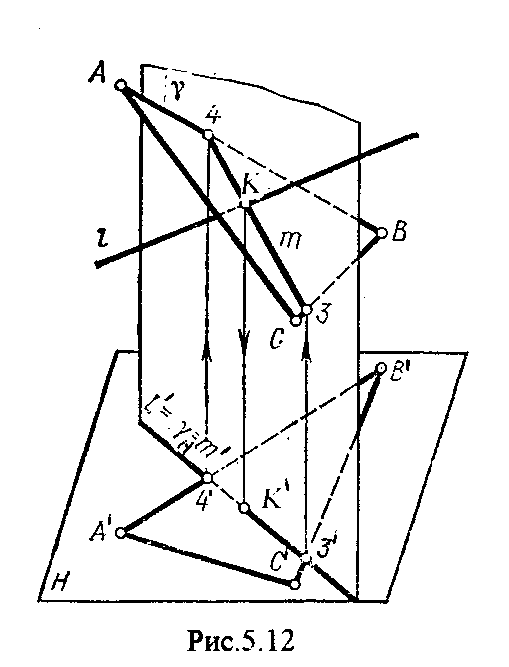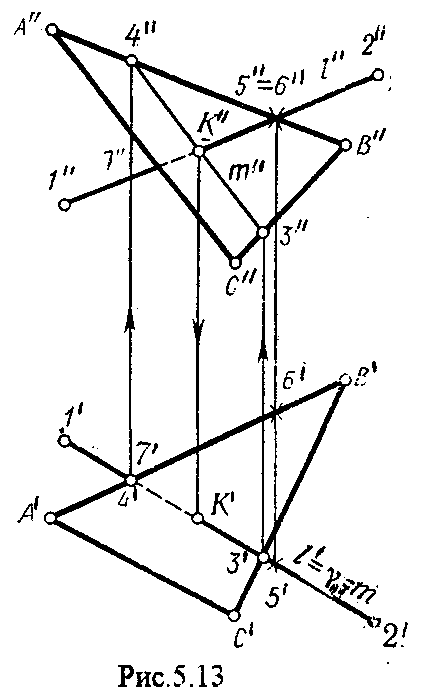




Через прямую 1 проведена вспомогательная горизонтально-проецирующая плоскость. Её горизонтальный след пересекается с АВ и АС в точках 3 и 4, определяющих горизонтальную проекцию а линии пересечения  и . Затем находим 3 и 4 и проводим проекцию m. В пересечении m и 1 - определяет фронтальную проекцию К искомой точки К. К определяем по условию принадлежности К  1.

Считая что плоскость непрозрачна определяем видимые и невидимые участки прямой 1 относительно плоскостей Н и V.

Для этого рассмотрим конкурирующие точки. Например: 5 и 6, 51, 6АВ.

По расположению горизонтальных проекций 5 и 6 заключаем, что участок прямой 2К находится перед плоскостью  и является на фронтальной проекции видимым. Остальная часть линии невидимая.

Аналогично, с помощью конкурирующих точек 7 и 4 определяем участки прямой на горизонтальной проекции. По расположению фронтальных проекций 7 и 4 заключаем, что участок прямой К1 расположен ниже плоскости , следовательно, невидимый на горизонтальной проекции.

Э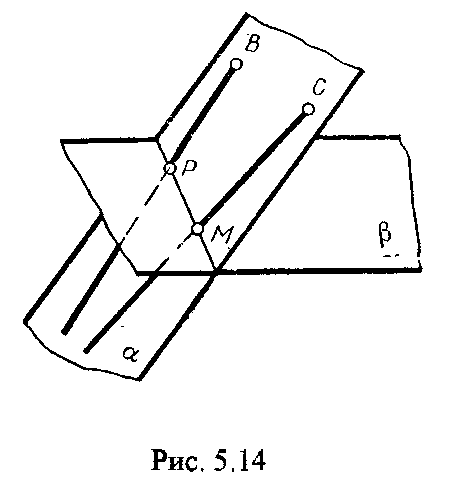
Рис.5.14.
тот алгоритм используется при определении линии пересечения двух плоскостей. Точки, принадлежащие линии пересечения определяются в пересечении прямых принадлежащих плоскости  с плоскостью  (рис.5.14).

На рис. 5.15 точки Р и М. Р является пересечением АВ и АС с треугольником DEF.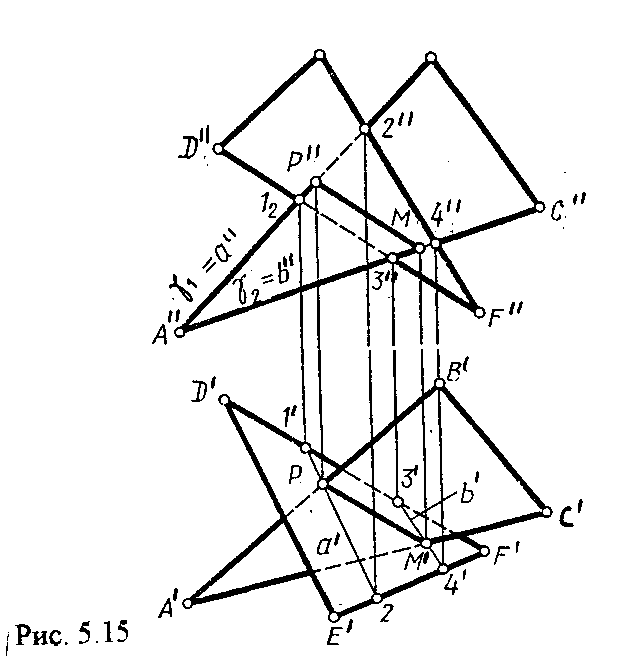



6. МЕТОДЫ ПРЕОБРАЗОВАНИЯ

Решение многих задач по начертательной геометрии сводится к определению позиционных и метрических характеристик геометрических фигур. В связи с этим все многообразие задач может быть отнесено к двум группам:

1. Задачи позиционные - решение которых должно дать ответ на вопрос о взаимном расположении геометрических фигур.

2. Задачи метрические - отвечают на вопросы метрики геометрических фигур, т.е. определение расстояний, величин углов, натуральных величин геометрических объектов и т.д.

В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависят от того, с какими проекциями (удобными или неудобными) приходится иметь дело. Задачи решаются зна-чительно проще в случае частного положения геометрической фигуры относительно плоскости проекции. При этом наиболее выгодным частным положением проецируемой фигуры следует считать:

а) положение, перпендикулярное к плоскости проекции (для решения позиционных, а в ряде случаев, и метрических задач);

б) положение, параллельное по отношению к плоскости проекции (при решении метрических задач).

Переход от общего положения геометрической фигуры к частному можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это достигается двумя путями:

во - первых, перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве;

во - вторых, перемещением плоскостей проекций в новое положение, по отношению к которому проецируемая фигура (которая не меняет своего положения в пространстве) окажется в частном положении.

Первый путь лежит в основе метода плоскопараллельного перемещения; второй составляет теоретическую базу метода перемены плоскостей проекций.
6.1. Метод плоскопараллельного перемещения

Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем перемещения геометрической фигуры в новое положение так, чтобы траектории перемещения ее точек находились в параллельных плоскостях.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида траектории метод плоскопараллельного перемещения подразделяют на способы:

а) способ параллельного перемещения.

Плоскости - носители траекторий перемещения точек параллельны какой - либо плоскости проекции. Траектория - произвольная линия;

б) способ вращения вокруг оси, перпендикулярной к плоскости проекций.

Плоскости - носители траектории перемещения точек параллельны плоскости проекции. Траектория - дуга окружности, центр которой находится на оси, перпендикулярной плоскости проекций;

в) способ вращения вокруг оси, параллельной плоскости проекций (вращение вокруг линий уровня);

г) способ вращения вокруг оси, принадлежащей плоскости проекций (вращение вокруг следа плоскости).

6.1.1. Способ параллельного перемещения

При параллельном переносе геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруэнтной проекции в ее исходном положении.

Пример 1. [АВ] прямой общего положения, перевести в положение, параллельное V (Рис.6.1.).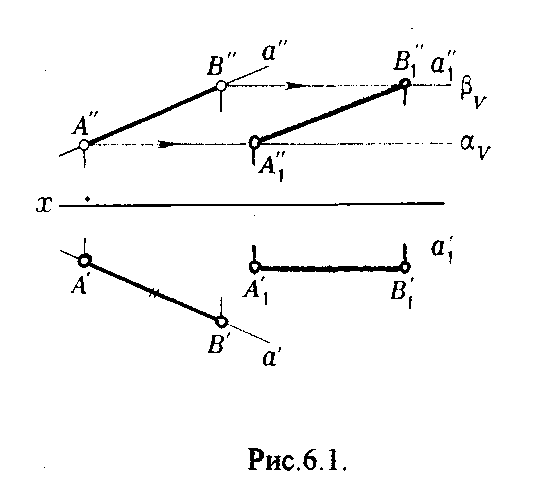



Рис.6.1.


У отрезка АВ, параллельного V, горизонтальная проекция должна быть параллельно оси х.

Перемещаем АВ в новое положение, причем АВ = A₁B₁. Фронтальные проекции точек А, В будут перемещаться по прямым, параллельным оси х. Полученные точки А₁, B₁ являются концами фронтальной проекции [АВ], параллельного V.

П 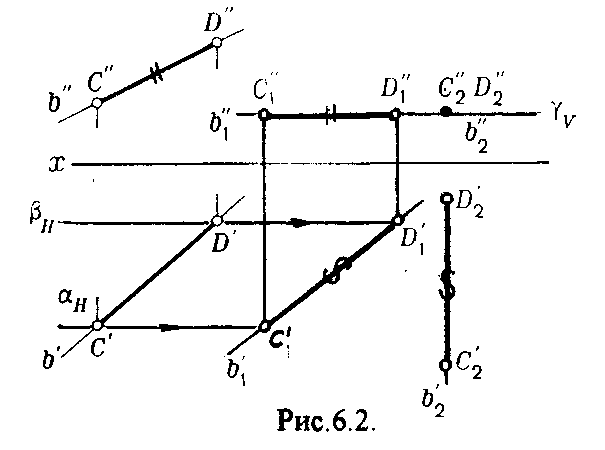ример 2. [АВ] перевести в положение, перпендикулярное V (Рис.6.2.).

Для перевода отрезка из общего положения в проецирующее, необходимо последовательно выполнить два перемещения: вначале перевести его в положение, параллельное Н, затем переводят отрезок в положение, перпендикулярное V.

Пример 3. Определить НВ треугольника ABC (Рис.6.3.).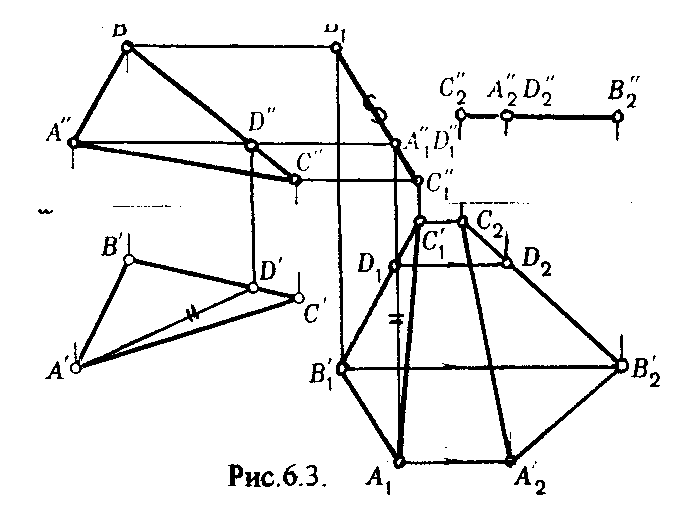

Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, легко перевести плоскость в частное положение. Для этого заданную плоскость надо рассматривать как множество линий уровня (фронталей и горизонталей).

Как видно из рис.6.3., в результате первого перемещения треугольник ABC займет фронтально - проецирующее положение, т.к. все горизонтали треугольника перпендикулярны V.

Второе перемещение осуществляем параллельно V, плоскость треугольника переведена таким образом в положение, параллельное плоскости Н.

6.1.2. Способ вращение вокруг оси, перпендикулярной

к плоскости проекции

Это частный случай параллельного перемещения. Отличие в том, что траектория перемещения каждой геометрической фигуры представляет собой не произвольную линию, а дугу окружности, центр которой находится на этой оси вращения, а радиус равен расстоянию между точкой и осью вращения.

При вращении вокруг оси, перпендикулярной V, точка будет перемещаться в плоскости, перпендикулярной оси вращения, а следовательно, параллельной Н. Окружность, по которой движется точка, проецируется, таким образом, на V без искажения, а на Н в отрезок, параллельный оси х.

Пример 1. [АВ] перевести в положение, параллельное V (Рис.6.4.).

В 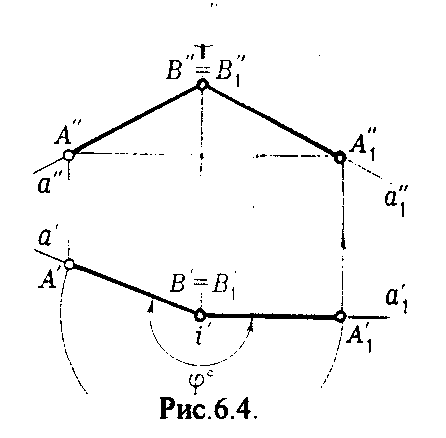ращение производили вокруг оси i  H. Ось i для упрощения геометрических построений проведена через точку В, следовательно она не будет менять своего положения в процессе преобразования. Для нахождения точки А^// необходимо из А^/ провести перпендикуляр к оси х и отметить точку его пересечения с горизонтальной прямой, проведенной через a^//.


Пример 2. [CD] перевести в положение, перпендикулярное V (Рис.6.5.).

В этом случае следует осуществить два вращения вокруг осей, перпендикулярных плоскостям проекций.

В 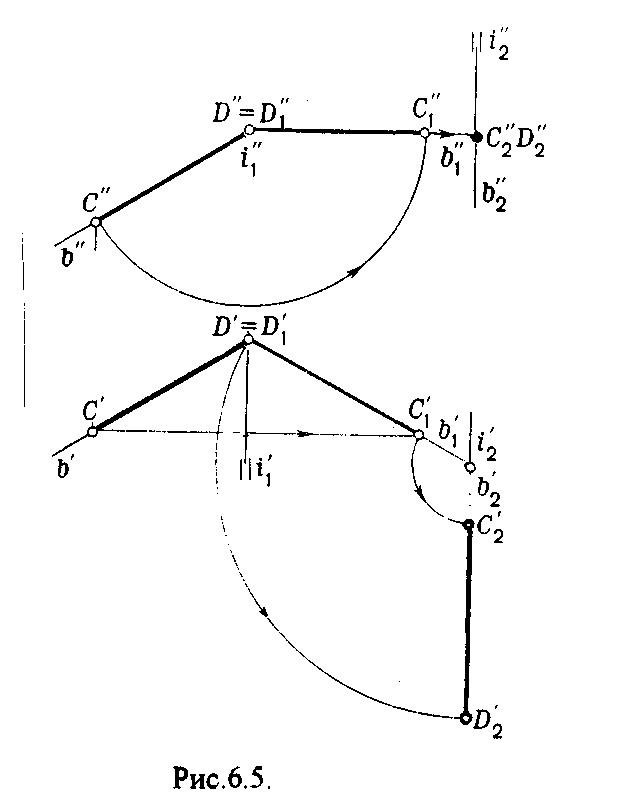начале вращение производим вокруг i₁V, в результате которого [АВ] занимает положение, параллельное Н, а затем переводим [АВ] в горизонтально - проецирующее положение вращением вокруг оси перпендикулярной Н.

В случае перевода плоскости общего положения в частное решается аналогично.

Чтобы плоскость общего положения заняла проецирующее положение, достаточно горизонталь или фронталь перевести в проецирующее положение. При повороте линии уровня на угол  на такой же угол повернется и все множество точек этой плоскости.

Если необходимо преобразовать плоскость в положение, параллельное плоскости проекции, необходимо осуществить еще одно вращение на какой - то угол так, чтобы вырожденная проекция плоскости (прямая, в которую проецируется плоскость) заняла положение, параллельное оси х..

6.2. Метод перемены плоскостей проекций.

Сущность метода перемены (замены) плоскостей состоит в переходе от данной системы плоскостей проекций к новой. При этом геометрические фигуры в процессе преобразования остаются на месте, а их новые проекции получаются за счет введения дополнительных плоскостей проекций. Новые плоскости выбираются перпендикулярно старым.

При выборе положения новой плоскости проекции следует руководствоваться тем, чтобы проецируемая фигура занимала частное положение относительно новой плоскости.

Р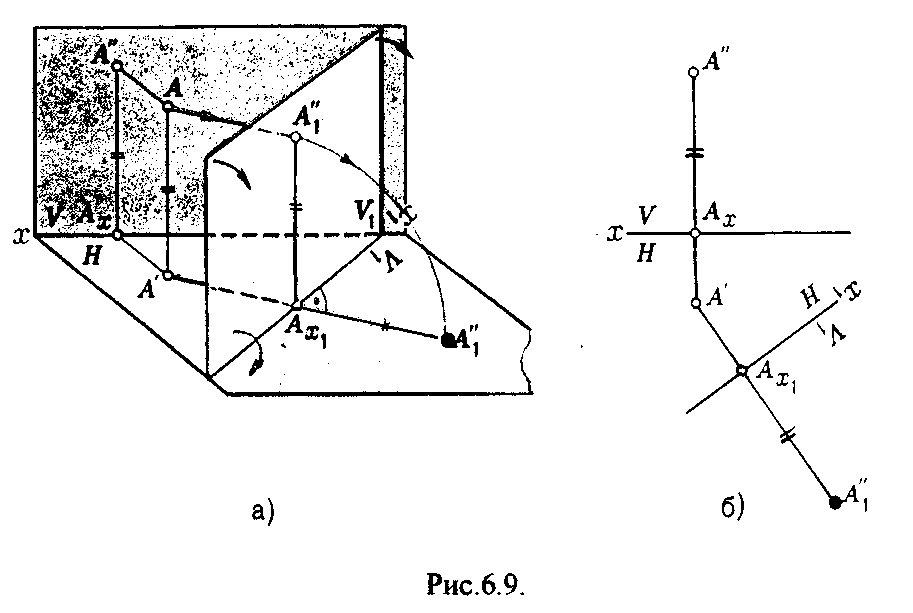
Рис.6.6.
ассмотрим изменение положения точки А, если V заменить новой плоскостью V₁(V₁ H). Горизонтальная плоскость не меняет своего положения, т.е. мы осуществляем переход от системы x(V/H) к новой x₁(V₁/H) (рис.6.6.а.). Плоскость V₁ пересекает Н по прямой х₁ т.е. по новой оси.

Горизонтальная проекция А не изменяет своего положения. Для нахождения новой фронтальной проекции А₁ следует провести линию связи перпендикулярно x₁ от А₁. Из рис.6.6. видно, что расстояние от новой фронтальной проекции А₁ до новой x₁ равно расстоянию от старой фронтальной проекции А до старой оси х.

Совмещая V₁ с Н, перейдем от пространственной модели к эпюру. За ось вращения принимается х₁, направление поворота не влияет на результаты преобразования (рис.6.6.б.).

Иногда замена одной проекции не обеспечивает получения требуемого вида проекции, поэтому приходится переходить к замене двух плоскостей. Но одновременно меняется только одна плоскость проекции.

Пример 1.[АВ] перевести в положение, параллельно фронтальной плоскости проекций (Рис.6.7.).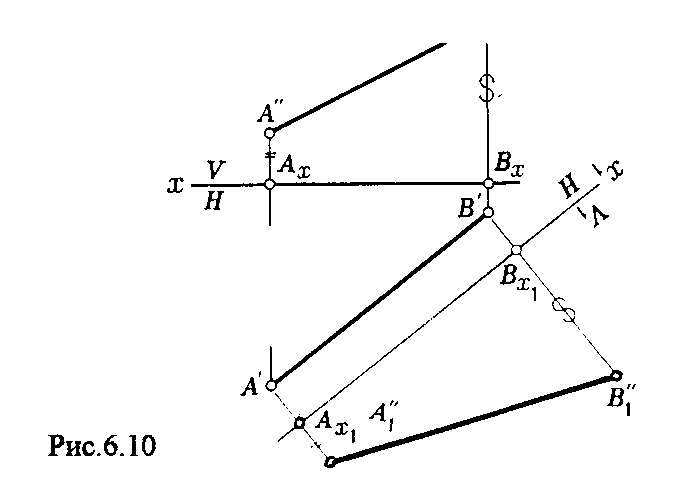




Рис.6.7.

Горизонтальная проекция прямой, параллельной фронтальной плоскости проекции, всегда параллельны оси х. Отсюда следует, что новую ось x надо выбирать параллельно А'В'. Остальные геометрические построения не требуют пояснений.

Пример 2. [АВ] перевести в горизонтально- проецирующее положение (Рис.6.8.).

В 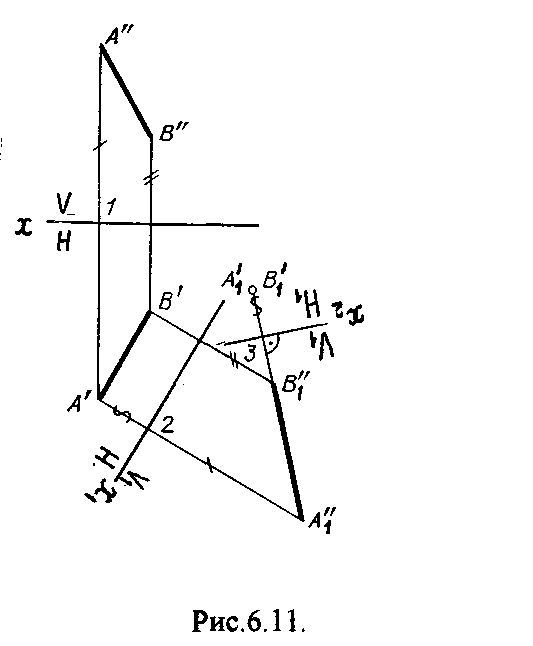этом случае следует произвести замену плоскостей дважды. Сначала меняем горизонтальную плоскость Н на новую H₁, т.е. переходим к системе x₁(V/H₁). В результате этого преобразования отрезок [АВ] займет положение, параллельное Н. Затем произведем замену старой фронтальной плоскости V на V₁, т.е. перейдем к системе x₂(V₁/H₁).

П
Рис.6.8.
оложение новой фронтальной проекции точки на плоскости V₁ определяется аналогично только что рассмотренному примеру. Отличие состоит лишь в том, что теперь за исходную (старую) систему будем принимать x₁(V/H₁) и от нее переходить к системе x₂(V₁/H₁). В этом случае плоскость h₁ не меняет своего положения в пространстве, следовательно не изменится положение и горизонтальной проекции A₁'B₁'. Например, фронтальная проекция А₂" будет определена, если из a₁' восставить к оси х₂ и отложить на нем расстояние, равное расстоянию от старой оси x₁ до старой фронтальной проекции А₁".

П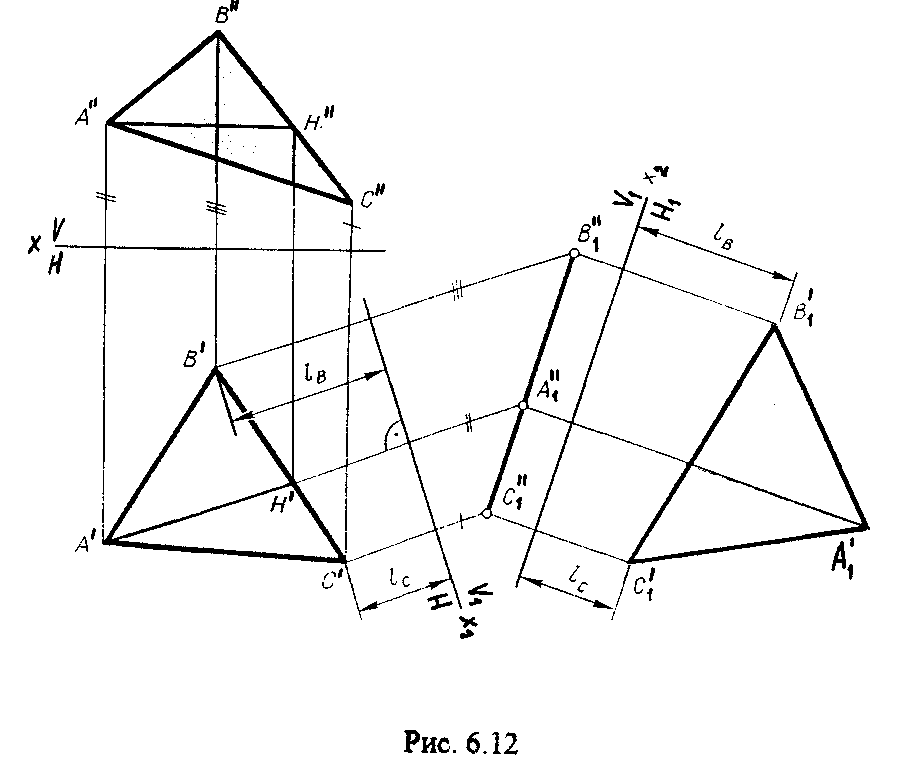
Рис.6.9.
ример 3. Определить натуральную величину треугольника ABC (рис.6.9.)

Для решения такой задачи следует провести две последовательные замены плоскостей. В начале произведем замену фронтальной плоскости проекций V на V₁ т.е. перейдем к новой системе координатных плоскостей X₁(V₁/H).

Новую ось X₁ выбираем перпендикулярно к горизонтальной проекции горизонтали h. Плоскость треугольника ABC рассматриваем в этом случае как множество горизонталей, которые проецируются в точке, лежащие на одной прямой.

В результате этого преобразования плоскость треугольника ABC займет проецирующие положение. Чтобы перевести плоскость треугольника ABC в положение плоскости уровня (в этом случае треугольник ABC будет проецироваться в НВ), следует провести еще одну замену плоскостей, т.е. перейти к системе X₂(V₁/H₁). Ось Х₂ проходит параллельно новой проекции А₁В₁С₁.

Остальные геометрические построения не требуют пояснения.

7. КРИВЫЕ ЛИНИИ И ИХ ПРОЕКЦИОННЫЕ СВОЙСТВА.

7.1. Основные понятия и определения

Кривую линию можно представить как траекторию точки, перемещающейся в пространстве или на плоскости,

Кривая линия так же может быть получена в результате пересечения поверхности с плоскостью или двух поверхностей между собой,

Кривые линии могут быть плоские, т.е. такие, все точки которых принадлежат одной плоскости и пространственные, точки которых не принадлежат одной плоскости.

Примерами плоских кривых являются: окружность, эллипс, парабола. Примером пространственной кривой является винтовая линия,

Линия считается закономерной, если в своем образовании она подчинена какому - нибудь закону.

Если, при этом, кривая в декартовой системе координат определяется алгебраическим уравнением, то она называется алгебраической. Примерами алгебраических кривых являются окружность, эллипс, парабола, гипербола. Степень уравнения кривой определяет порядок кривой.

Кривая линия определяется положениями составляющих ее точек, Точки кривой определяются их координатами.

На чертеже кривая задается своими проекциями. Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить их между собой в той же последовательности, в какой они располагались на оригинале, При задании кривой ее проекциями необходимо указать, по крайней мере, проекции одной точки, принадлежащей кривой (рис.7.1.).

По чертежу кривой в общем случае можно без дополнительных построений определить пространственная она или плоская. На рис.7.1. кривая а пространственная, т.к. она имеет конкурирующие точки С, D. Если по чертежу не понятно, плоская кривая или пространственная, требуются дополнительные построения. На кривой нужно выбрать три произвольные точки и проверить, лежит ли любая четвертая точка кривой в плоскости, определяемой первыми тремя. Кривая m, изображенная на рис.7.2. пространственная, т.к. точка М(М, М) не лежит в плоскости  заданной точками А, В, С этой кривой.
7 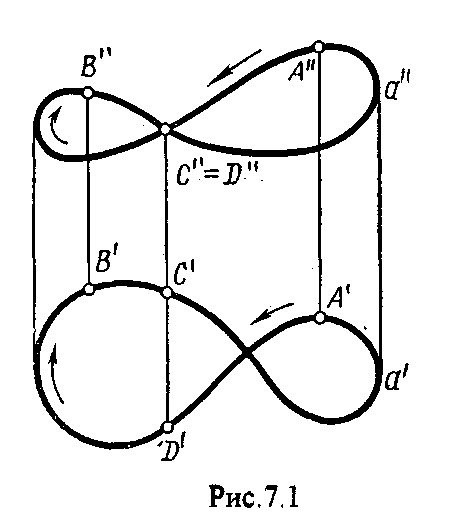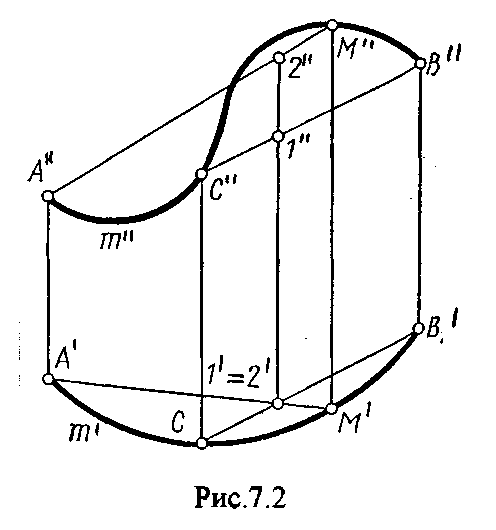.2. Некоторые свойства проекций пространственных и

плоских кривых

Если точка А принадлежит кривой m, то проекция этой точки А принадлежит проекции m кривой. Секущая и касательная к кривой проецируются соответственно в секущую и касательную к проекции кривой. Пусть через точку А кривой m проведена секущая n (рис.7.3.).

П 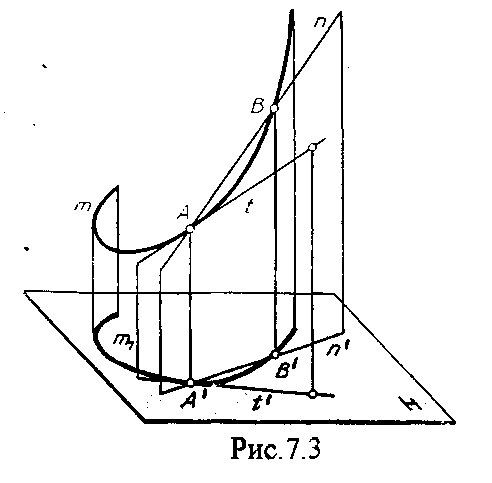роекция секущей определяется точками А и В принадлежащими проекции m рассматриваемой кривой. Прямая n, пересекающая проекцию кривой, является по отношению к m секущей. Касательную t можно рассматривать как предельное положение секущей, которое занимает последняя при сближении точек пересечения А и В в одну точку, В этом случае совпадут друг с другом и их проекции, т.е. проекция n секущей превратиться в касательную t к проекции m кривой.

7.3. Проекции плоских кривых

Чтобы наиболее точно передать форму кривой линии, при построении ее проекций необходимо, прежде всего, отложить характерные точки. Такими точками являются особые точки кривой, а так же точки наиболее удаленные от плоскостей проекций и наиболее близкие к ним.

Точка кривой называется обыкновенной, если в этой точке к кривой можно провести единственную касательную. На рис.7.4. такой точкой является точка М.

Д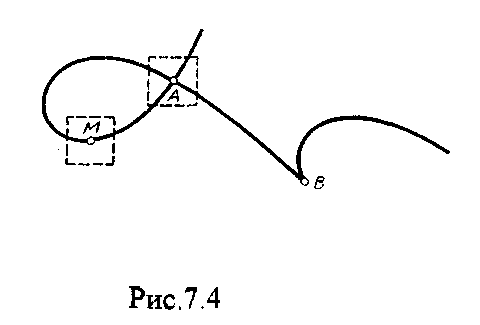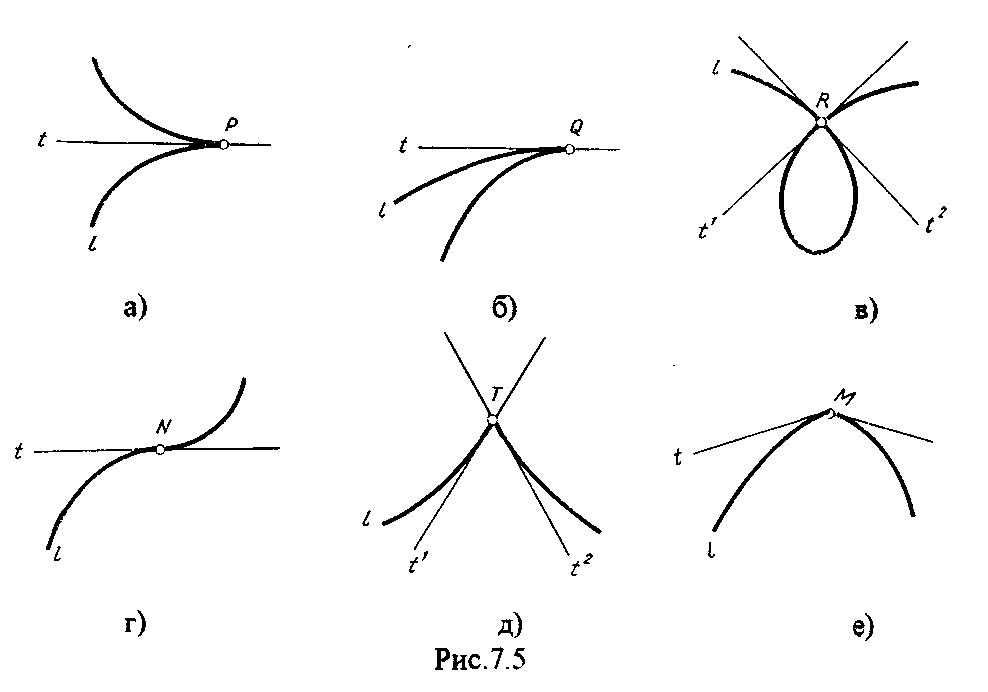
Рис.7.4.
ругие точки называют особыми (точки А, В). К ним относятся точки возврата (рис.7.5,а,б.), точки самопересечения (рис.7.5,в.), точки перегиба (рис.7,5,г.), точки излома (рис.7.5,д,е.).Особым точкам плоской кривой соответствуют такие же точки на ее проекции. Кривая, состоящая только из обыкновенных точек, называется плавной кривой.

Н 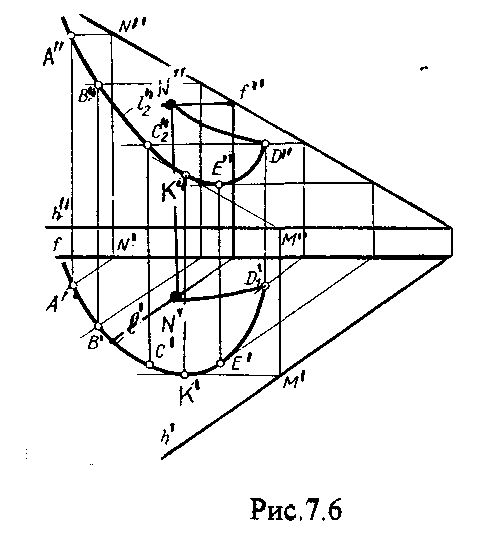а рис.7.6. выполнено построение горизонтальной проекции l кривой линии 1, принадлежащей плоскости (h,f) по заданной фронтальной 1. Точки А, К, N, D, Е - характерные. А - точка, наиболее удаленная от горизонтальной плоскости проекции, К - точка, наиболее удаленная от фронтальной плоскости проекций, Е - самая низкая, D - точка возврата, N - точка прекращения.

Точки В, С - промежуточные. Все точки кривой строятся по условию принадлежности их плоскости.

7.3.1. Изображение окружности на комплексном чертеже

Рассмотрим три случая.

1. Окружность 1 лежит в плоскости уровня  (рис,7.7.) В этом случае она проецируется на одну из плоскостей проекций в натуральную величину, а на другой плоскости совпадает со следом плоскости _V.

H 1- натуральная величина l = _V.

2. Окружность 1 лежит в проецирующей плоскости  (рис,7,8.). Одна из ее проекций совпадает со следом плоскости, _V вторая проекция эллипс.

l, l = _V; АВ - большая ось эллипса АВ = 2R, CD - малая ось.

3. Окружность 1 лежит в плоскости общего положения (рис.7.9.) проецируется на обе плоскости в эллипсы.

Большие оси эллипсов l, l принадлежат линиям уровня, соответственно горизонтали и фронтали, и по длине равны диаметру окружности 1. Поэтому большую ось АВ эллипса l на Н откладываем на горизонтальной проекции h горизонтали, большую ось МN эллипса l - на фронтальной проекции f фронтали.

А, В, М, N находим по условию принадлежности их горизонтали м фронтали. Малые оси эллипсов принадлежат линиям наибольшего наклона. Для построения малых осей CD и РQ проводим nАВ и mMN.

7 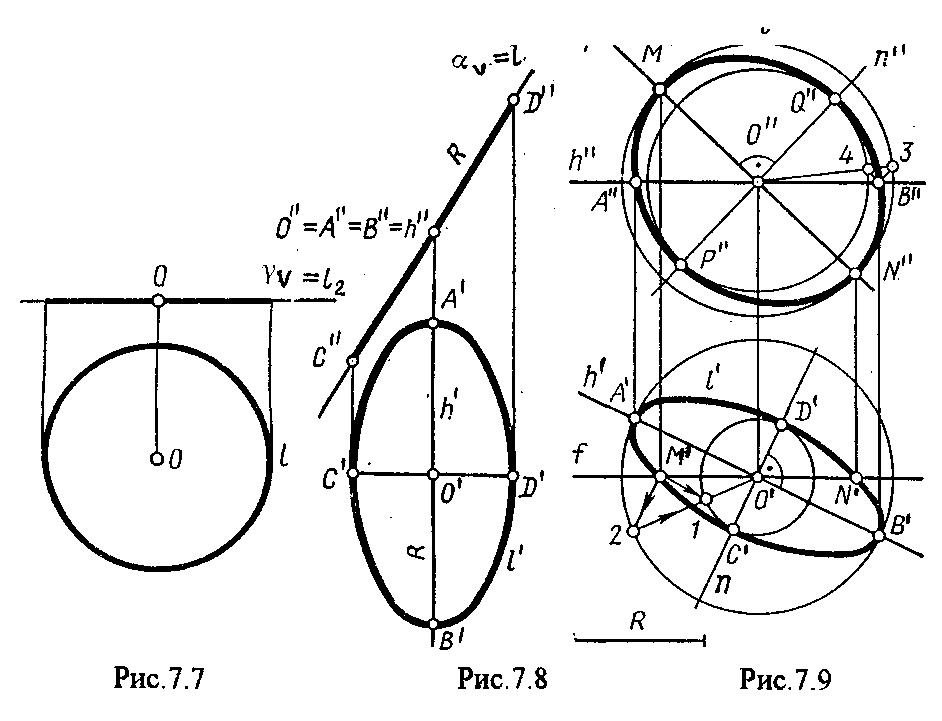.4. Винтовые линии

Наиболее часто встречающаяся в инженерной практике пространственная кривая - это цилиндрическая винтовая линия. (Рис.7.10.)

Цилиндрическая винтовая линия представляет собой траекторию точки, которая совершает равномерное поступательное движение вдоль оси равномерного вращающегося цилиндра. Ось цилиндра будет осью винтовой линии, а радиус его - радиусом винтовой линии. Расстояние Р., на которое точка перемещается вдоль оси цилиндра за один его оборот, называется шагом винтовой линии.

Для построения проекции винтовой линии предварительно строим проекции прямого кругового цилиндра (рис.7,11). Окружность основания цилиндра (горизонтальная проекция) и шаг (фронтальная проекция) делит на одинаковое число равных частей. Из точек деления окружности проводим линии связи, а через соответствующие точки деления шага горизонтальные прямые.

Отмечаем точки 1, 2, 3 ... 8, в которых пересекаются соответственные прямые. Соединив, их плавной кривой, получим фронтальную проекцию винтовой линии.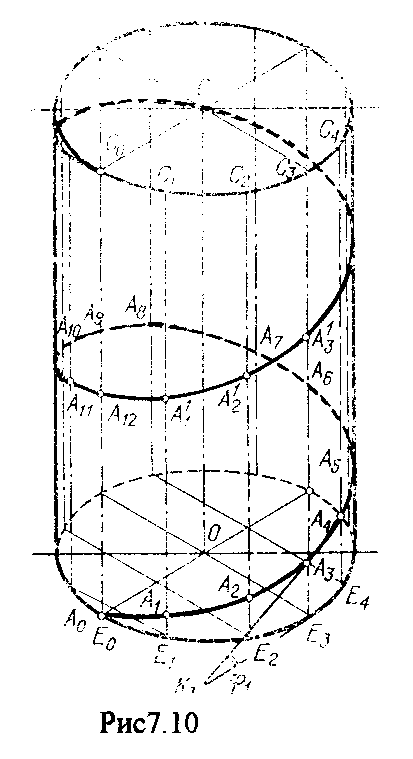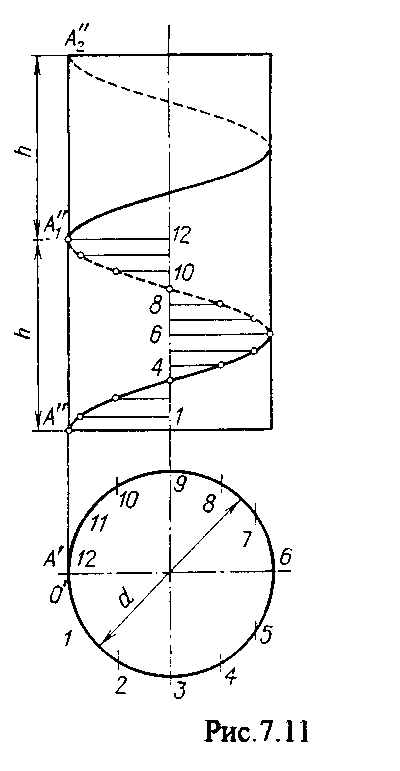




Рис.7.10.


Рис.7.11.


Р 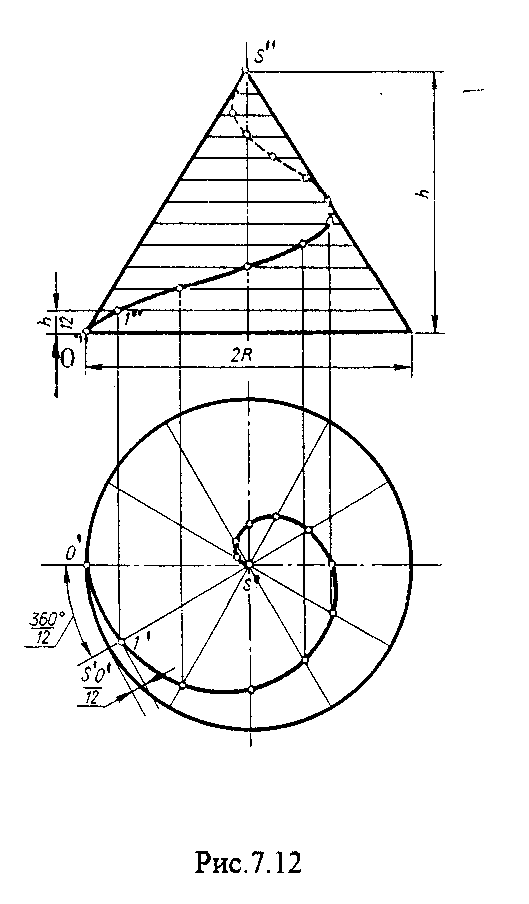азличают правую и левую винтовые линии.

Если наблюдатель смотрит вдоль винтовой линии и видит ее при подъеме закручивающейся против часовой стрелки, то винтовая линия называется правой.

Если точка перемещается равномерно по обра-зующей прямого кругового конуса, а образующая совершает вращательное движение вокруг оси конуса с постоянной скоростью, то траекторией точки является коническая винтовая линия.


Рис.7.12.

8. ПОВЕРХНОСТИ

Поверхности - это бесконечное разнообразие геометрических фигур. Любой предмет в природе или в технике ограничивается своей поверхностью. Инженерная деятельность связана непосредственно с конструированием, расчетом, изготовлением различных технических поверхностей.

8.1. Способы образования и задания поверхностей,

определитель поверхности, каркас поверхности

Поверхность можно представить как общую часть двух смежных областей пространства. В начертательной геометрии поверхность определяется как совокупность последовательных положений линии, перемещающейся в пространстве по определенному закону. Такой способ образования поверхности называется кинематическим. Линия, перемещающаяся в пространстве, называется образующей. Образующая может быть прямой линией или кривой. Она может иметь постоянную форму или менять ее в процессе перемещения. Закон перемещения в пространстве образующей удобно задавать в виде совокупности неподвижных линий. Их называют направляющими. Процесс образования поверхности показан на рис.8.1.

О 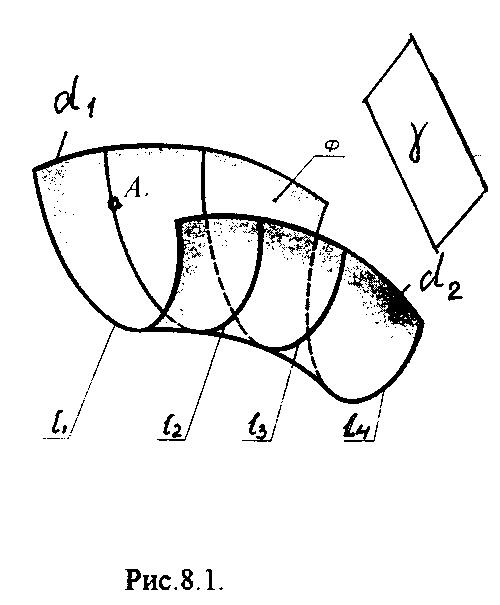бразующей является кривая 1. Закон перемещения задан двумя направляющими d₁, d₂ и плоскостью . Обра-зующая 1 скользит по направ-ляющим d₁ и d₂, оставаясь параллельной плоскости , Точка А, принадлежащая поверхности принадлежит 1₂.

П
Рис.8.1.
оверхность определена, если можно однозначно решить, принадлежит точка пространства данной поверхности или нет. Совокупность условий, задающих поверх-ность в пространстве и на чертеже, называется опре-делителем поверхности.

Определитель состоит из двух частей геометрической и алгоритмической. Геометрическая часть определителя это перечень геометрических элементов, участвующих в образовании поверхности. Алгоритмическая часть - указывает на взаимосвязь между элементами.

Одна и та же поверхность может быть образована разными способами, поэтому может иметь различные определители. Например, поверхность прямого кругового цилиндра можно представить:

а) как результат вращения прямой 1 при ее вращении вокруг оси i С (1, i); [вращение 1 вокруг i];

б) как результат вращения кривой k, точки которой равноудалены от оси i, вокруг оси i. С (k., i); [ вращение k вокруг i];



в 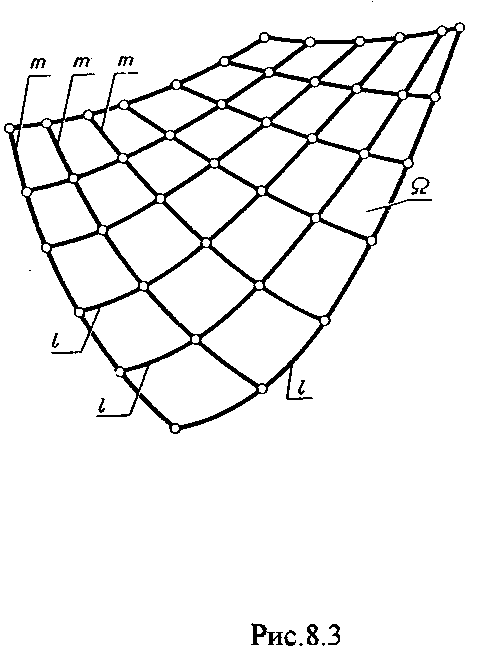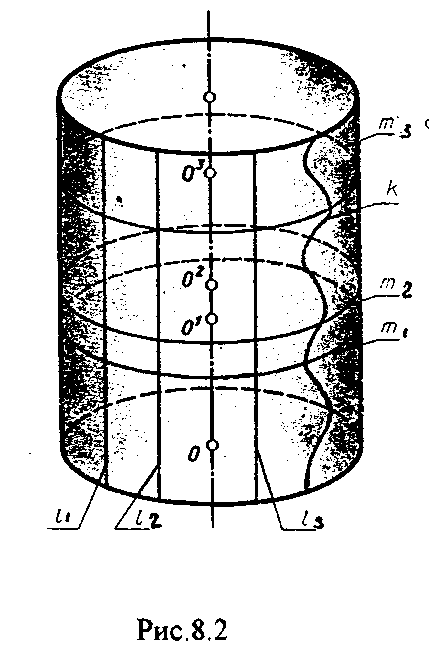) как результат поступательного перемещения окружности m. При этом центр окружности 0 перемещается по оси i, а ее плоскость  остается перпендикулярной к оси i C(m.i); [ поступательное, 0  i, 1  i]. Из множества определителей выбирают наиболее простой. В данном случае - вариант (а).

У
Рис.8.3.
порядоченное множество точек или линий, принадлежащих поверхности называется ее каркасом (рис.8.3). Каркас поверхности может быть точечным или линейным. Линейным каркасом называется множество линий имеющих единый закон образования и связанных между собой определенной зависимостью. Эта зависимость называется параметром каркаса. Если параметр каркаса непрерывная функция, каркас называется непрерывным, т.е. через любую точку поверхности проходит одна линия.

Каркасом задают сложные поверхности технических объектов, таких как обшивки самолетов, автомобилей, судов, лопатки турбин, насосов. Каркасные поверхности задают на чертеже проекциями элементов каркаса (рис.8.4.).

К 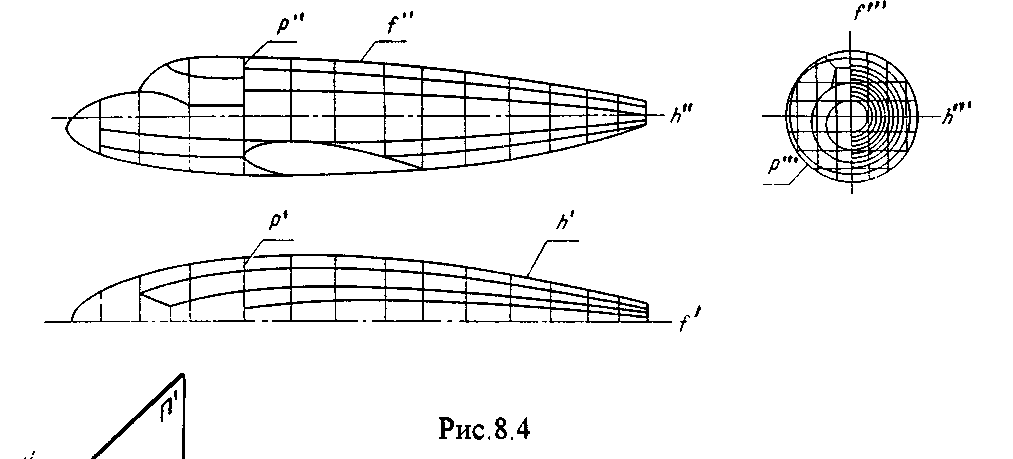аркас таких поверхностей называется дискретным. В этом случае положение точки, не принадлежащей линии каркаса можно определить только приближенно.

З
Рис.8.5.

Рис.8.4.
адание поверхности проекциями определителя не всегда обеспечивает нагляд-ность, что затрудняет чтение чертежа. Для придания чертежу поверхности нагляд-ности его дополняют очер-ковыми линиями очерком поверхности (при ортого-нальном проецировании) называют след на плос-кости проекции проецирующей цилиндрической поверхность, которая огибает данную поверхность. Рис.8.5.

8.2. Классификация поверхностей

Многообразие поверхностей требует их систематизации. В основе систематизации лежат два признака: вид образующей и закон ее перемещения. По виду образующей поверхности делят на линейчатые (образующая прямая) линии и нелинейчатые ^образующая кривая). По закону перемещения поверхности параллельного переноса, вращения и винтовые.