Начертательная геометрия. Конспект лекций по курсу нгииг л. В. Белозерцева, А. Г. Коробова, М. Н. Потапова

• Название: Конспект лекций по курсу нгииг л. В. Белозерцева, А. Г. Коробова, М. Н. Потапова
• Анкор: Начертательная геометрия
• Дата: 29.03.2023
• Размер: 1.12 Mb.
• Имя файла: 310.doc
• Тип: Конспект лекций; #1024690
• страница: 2 из 4

С

Рис.1.5.

При ортогональном проецировании (как и при центральном и параллельном) однозначно решается задача по определению проекции фигуры по оригиналу. Для решения обратной задачи, т.е. воспроизведение оригинала по его проекции, необходимо иметь, по крайней мере, две ортогональные проекции оригинала.

1.5. Пространственная модель координатных плоскостей

проекций

Д 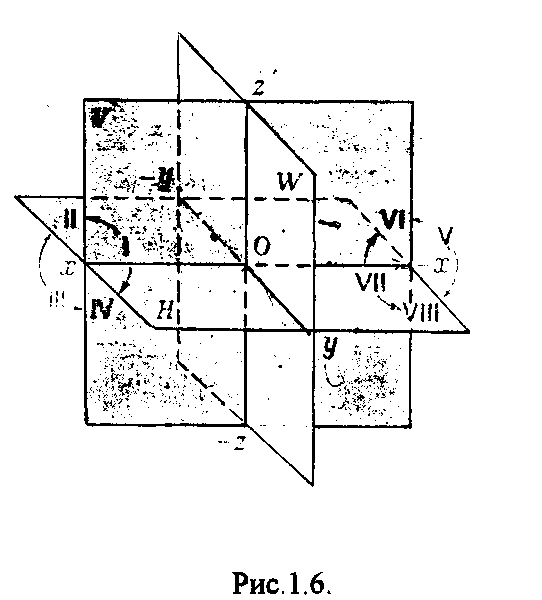ля определения положения геометрического объекта в пространстве необходимо задаться какой-либо координатной системой отнесения. Наиболее удобной является система координат, состоящая из трех взаимно перпендикулярных плоскостей.

Р
Рис.1.6.
ассмотрим макет из трех взаимно перпендикулярных плоскостей (рис.1.6.), которые делят пространство на 8 частей, называемых октантами:

Условимся называть:

плоскость Н -горизонтальная плоскость проекции;

плоскость V - фронтальная плоскость проекции;

плоскость W - профильная плоскость проекции.

Линии пересечения плоскостей проекций образуют оси координат. Ось х называют осью абсцисс, ось у - осью ординат и ось z -осью аппликат. Точка пересечения координатных осей принимается за начало координат.

Положительным направлением осей координат считают для оси х - влево от начала координат, для оси у - в сторону наблюдателя от начала координат, для оси z - вверх от начала координат. Противоположные направления осей считаются отрицательными.

1.6. Плоскостная модель координатных плоскостей (эпюр)

П 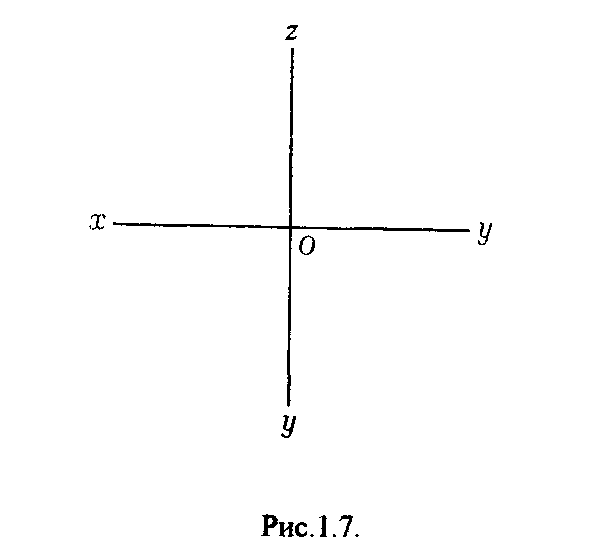ространственной моделью координатных плоскостей пользоваться на чертеже неудобно, поэтому ее преобразуют в эпюр, т.е. чертеж, составленный из двух или более связанных между собой проекций геометрической фигуры. Для этого горизонтальную и профильную плоскость проекции совмещают с фронтальной плоскостью проекции путем поворота плоскости Н на 90° вокруг оси х по часовой стрелке и плоскости W на 90° вокруг оси z против часовой стрелки. Отрицательное нап-равление осей на эпюре не указывается, и в окончательном виде эпюр, заменяющий пространственную модель, примет вид, показанный на рис. 1.7.

Октанты	Знаки координат
	X	У	z
I	+	+	+
II	+	—	+
III	+	-	—
IV	+	+	—
V	—	+	+
VI	-	-	+
VII	_	-	—
vni	-	+	-

Рис.1.7.

2. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ

Положение точки в пространстве определяется координатами (х, у, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций (рис.2.1.)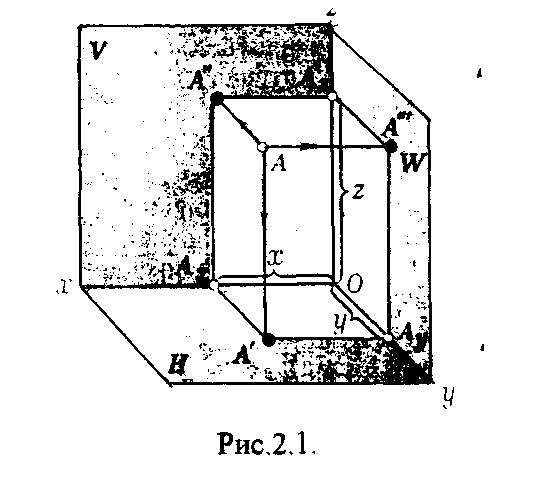



Рис.2.1.

Чтобы определить эти расстояния, достаточно через точку А провести прямые, перпендикулярные к плоскостям проекций, определить точки А', А", А'" встречи этих прямых с плоскостями проекций и измерить величины отрезков [АА'], [АА"3, [АА'"], которые укажут соответственно значения аппликаты z, ординаты у и абсциссы х точки А.

Точки А', А", А'" называют ортогональными проекциями точки А, при этом согласно принятым обозначениям:

А' - горизонтальная проекция точки А;

А" - фронтальная проекция точки А;

А'" - профильная проекция точки А.

Прямые (АА'), (АА"), (АА'") называют проецирующими прямыми или прое-цирующими лучами.

Эпюр точки А, представленный на рис.2.2., несет ту же информацию, что и пространственный макет. Горизонтальная проекция точки А определяется координатами х, у т.е. расстоянием от точки А до плоскостей W и V.

А'(х, у).

Фронтальная проекция точки А определяется координатами х и z, т.е. расстоянием от A floW и Н.

А"(х, z).

Профильная проекция точки А определяется координатами у и z, т.е. расстоянием от V и Н.

А'"(у, z).

А 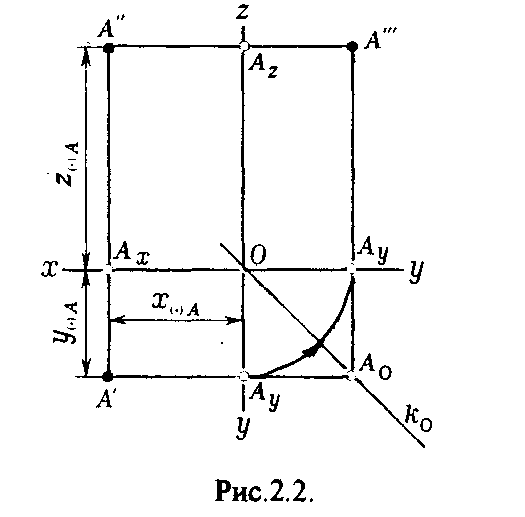нализируя рис.2.2., можно сделать следующие выводы: фронтальная и профильная проекции точки всегда находятся на одной горизонтальной линии связи; фронтальная и горизонтальная проекции точки всегда находятся на одной вертикальной линии связи. Таким образом, можно построить недостающую третью проекцию.

Октанты	Знаки координат
	X	У	Z
I	+	+	+
II	+	—	+
III	+	-	—
IV	+	+	—
V	—	+	+
VI	-	-	+
VII	_	-	—
VIII	-	+	-

Рис.2.2.
Положение точки в пространстве можно определить, если будут заданы хотя бы две ее координаты. Зная направление для положи-тельного и отрицательного значений координатных осей, определяется принадлеж-ность точки какому -либо из восьми октантов. Для этого можно составить следующую таблицу:

3. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПРЯМОЙ

Прямая линия определяется двумя точками, чтобы построить эпюр прямой, надо построить проекции лишь двух ее точек.

Прямая в пространстве может быть расположена относительно плоскостей проекций по-разному. Прямую, не параллельную и не перпендикулярную ни к одной из плоскостей проекций, называют прямой общего положения.

3.1. Следы прямой

Прямая общего положения пересекает все три плоскости проекций.

Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой. Точка пересечения прямой 1 с горизонтальной плоскостью проекций называется горизонтальным следом прямой l_h, с фронтальной - фронтальным следом прямой l_v, с профильной - профильным следом прямой l_w (рис.3.1.).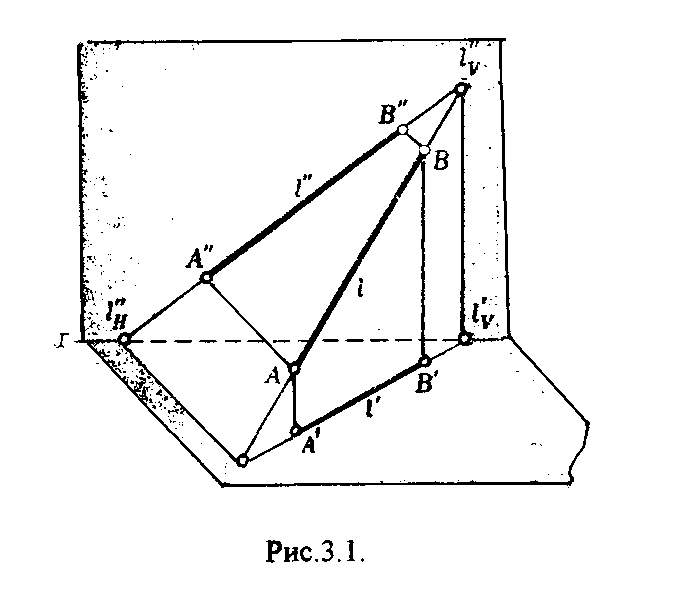



l_H, 1_H", 1_H, lv', lv", lv'", l_W', lw", lw'" - соответственно горизонтальная, фронтальная, профильная проекции следов 1_H, lv , lw. Очевидно, что 1_Н'= 1_H", lv"= lv , lw'"= l_W.

Чтобы построить на чертеже горизонтальный след прямой 1 (рис.3.2.), надо продолжить фронтальную проекцию прямой 1 до пересечения с осью х в точке 1н", затем, используя принцип принадлежности точки прямой достроить 1_Н'.

Для построения фронтального следа прямой 1 надо продлить горизонтальную проекцию прямой 1 до пересечения с осью х в точке lv' и достроить по соответствующим линиям связи l_V".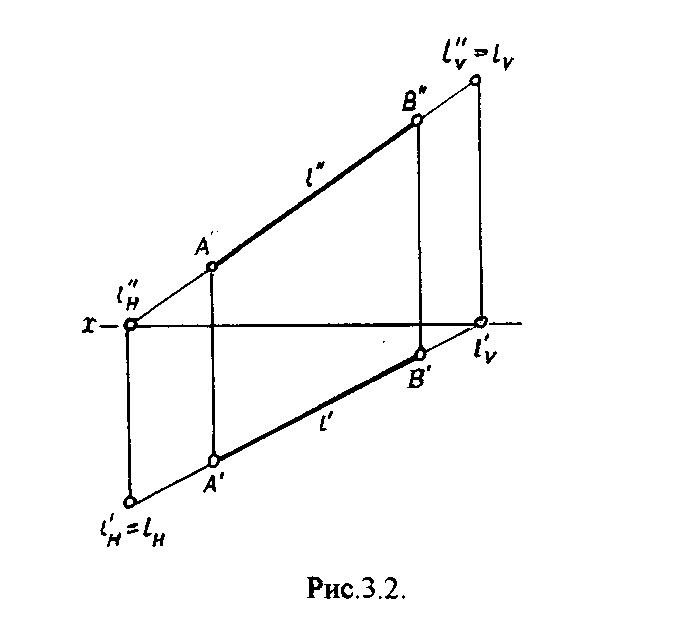




Аналогично строится профильный след прямой 1. Для этого продолжают либо фронтальную проекцию прямой I до пересечения с осью z в точке l_W", либо горизонтальную проекцию 1 до пересечения с осью у в точке l_W' и по соответствующим линиям связи достраивают недостающие проекции.

3.2. Прямые частного положения

Прямая может занимать по отношению плоскостям проекций частное положение:

а) параллельное плоскости проекции;

б) перпендикулярное плоскости проекции;

в) принадлежность плоскости проекции.
3.2.1. Прямые уровня

Прямые, параллельные плоскости проекций, называются прямыми уровня(рис.3.3.).

Горизонталь - прямая, параллельная горизонтальной плоскости проекций (рис.3.3.а.).

Фронталь - прямая, параллельная фронтальной плоскости проекций (рис.3.3.б.).

Профильная прямая - прямая, параллельная профильной плоскости проекций (рис.3.3.в.).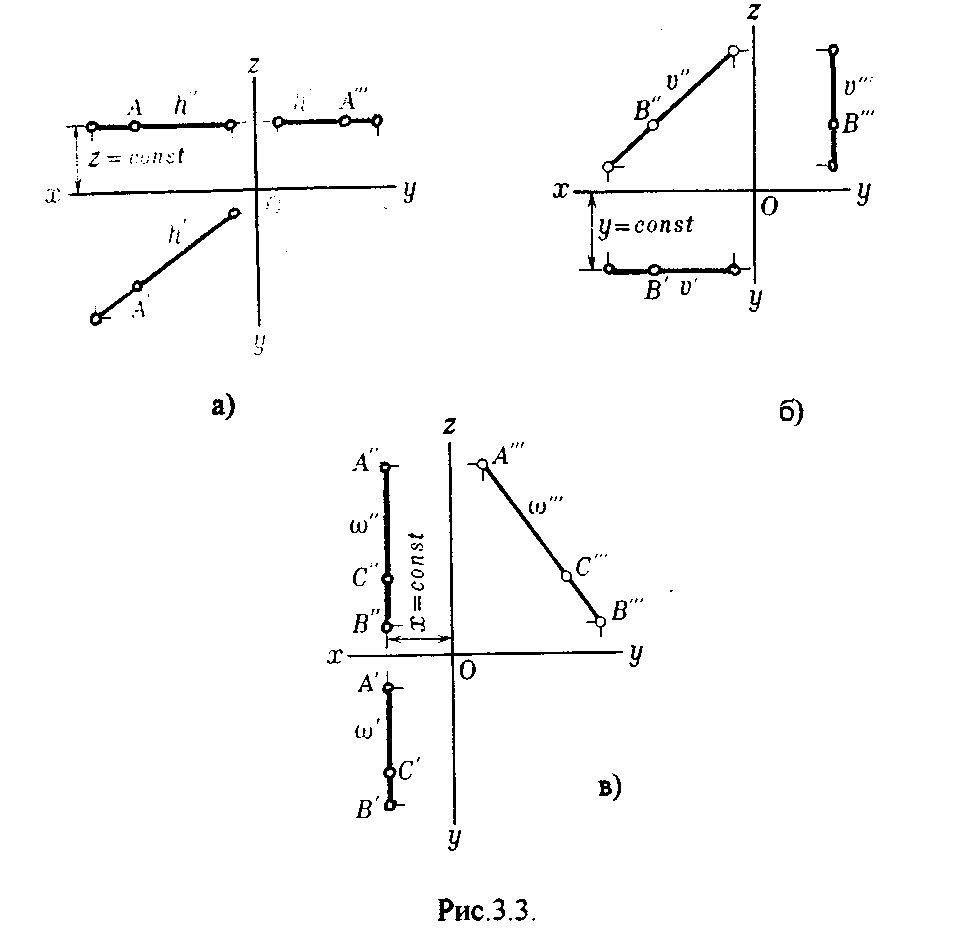




3.2.2. Проецирующие прямые

Прямые, перпендикулярные какой-либо плоскости проекции, называются проецирующими прямыми (рис.3.4.).

Прямые, перпендикулярные горизонтальной плоскости проекций, называются горизонтально — проецирующими прямыми (рис.ЗАа.).

Прямые, перпендикулярные фронтальной плоскости проекции, называются фронтально-проецирующими прямыми (рис.3.4.6.),

Прямые, перпендикулярные профильной плоскости проекций, называются профильно - проецирующими прямыми (рис.3.4.в.).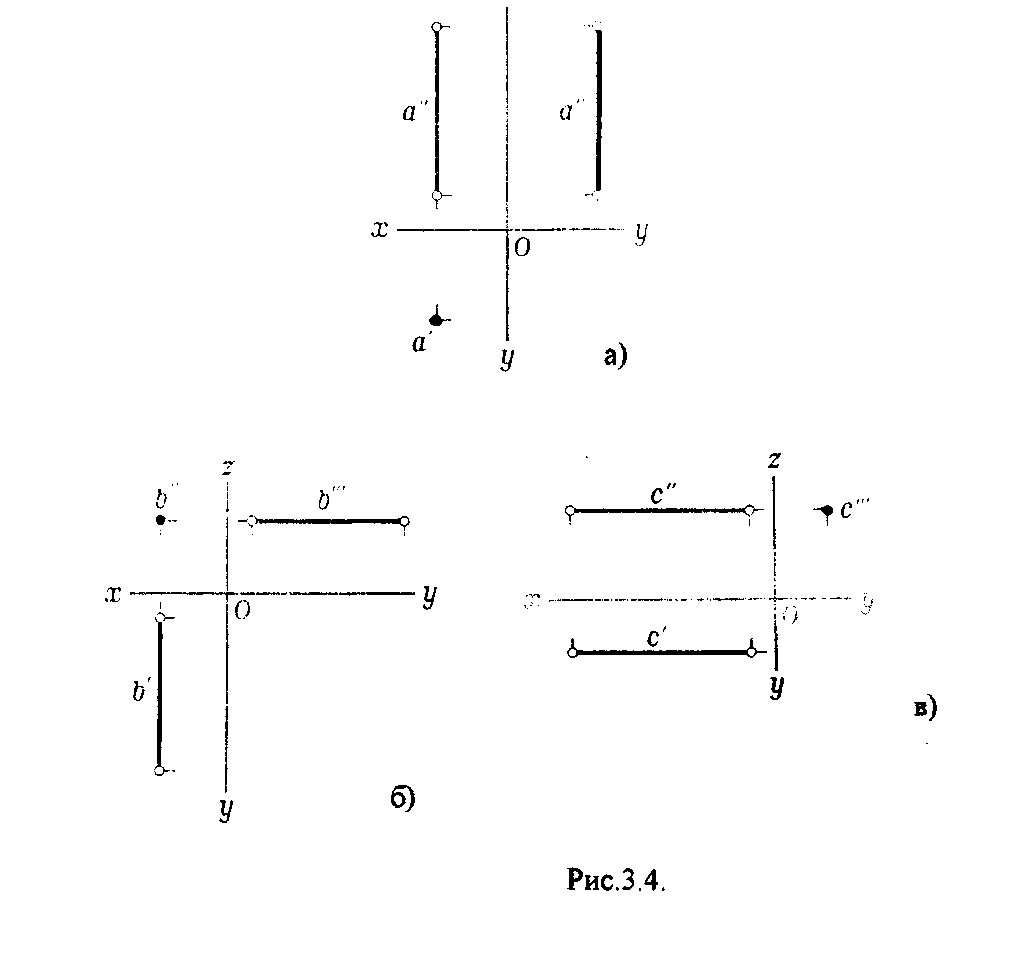

Октанты	Знаки координат
	X	У	z
I	+	+	+
II	+	—	+
III	+	-	—
IV	+	+	—
V	—	+	+
VI	-	-	+
VII	_	-	—
vni	-	+	-

3.2.3. Прямые, принадлежащие плоскости проекции

Это частный случай прямых уровня.

Характерным признаком таких прямых является принад-лежность двух проекций прямой координатным осям. На рис.3.5. показаны проекции прямых 1, т, п. Прямая 1 принадлежит горизонтальной плоскости проекции (рис.3.5.а.), прямая m –фрон-тальной плоскости проекции (рис.3.5.б.), прямая n -профильной плоскости проекции (рис. З.5.в.).

3 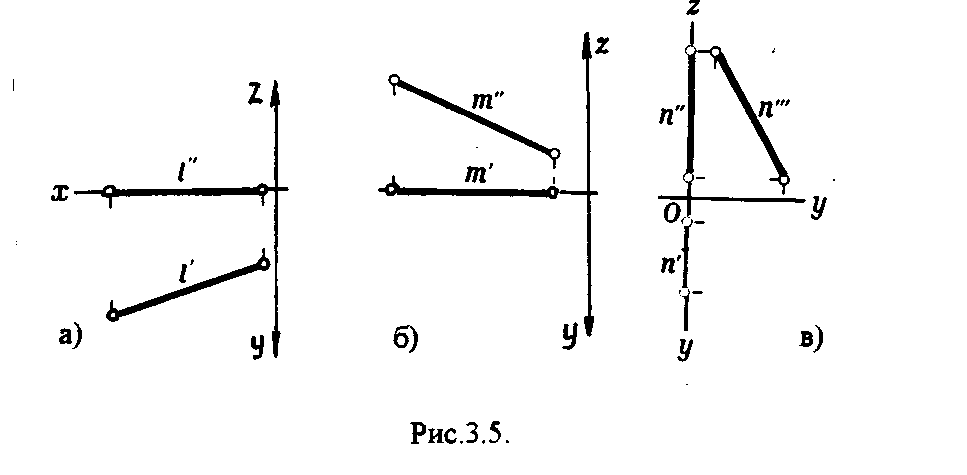.3. Взаимное положение прямых

Прямые в пространстве могут занимать различное взаимное положение: быть параллельными, пересекаться и скрещиваться.

Если прямые в пространстве параллельны то на чертеже параллельны их одноименные проекции (рис.З.б.а.). Справедливо и обратное утверждение.

Если прямые в пространстве пересекаются, то на чертеже пересекаются их одноименные проекции. При этом точки пересечения проекций этих прямых лежат на одной линии связи (рис.3.6.б.).

Если прямые в пространстве скрещиваются, то на чертеже их одноименные проекции могут и пересекаться, но точки пересечения этих проекций не лежат на одной линии связи (рис.З.б.в.).

Т 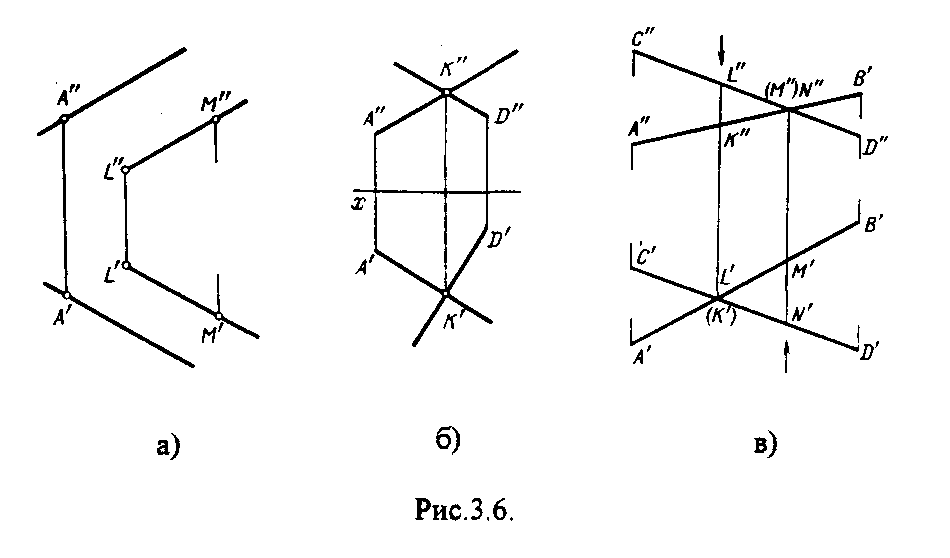очка пересечения одноименных проекций скрещивающихся прямых является на чертеже проекцией двух конкурирующих точек - заданных прямых.

3
а) б) в)

Рис.3.6.
.4. Определение натуральной величины отрезка

методом прямоугольного треугольника

Отрезки прямых общего положения ни на одну из плоскостей проекций не проецируется в натуральную величину (НВ).

Н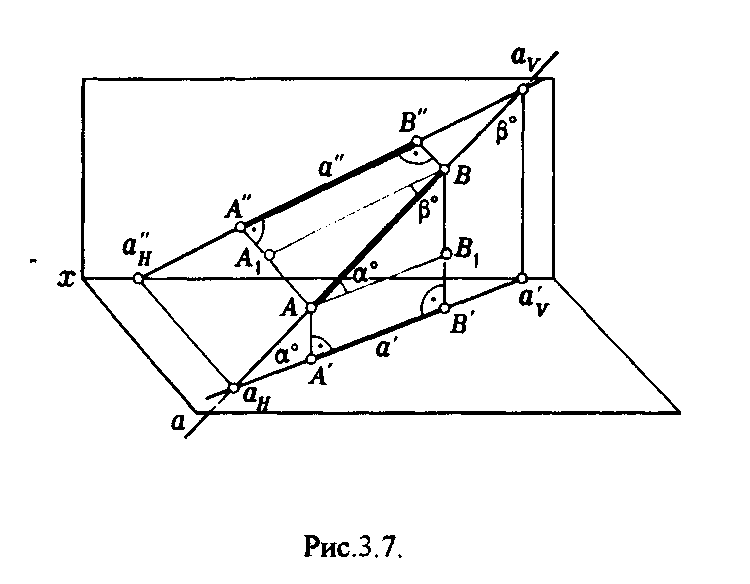
Рис.3.7.
атуральная величина отрезка общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а другим разность расстояний концов отрезка от этой же плоскости (рис.3.7.).

Из рисунка 3.7. видно, что угол наклона прямой к плоскости проекций определяется как угол, составленный прямой с ее проекцией на эту плоскость. Этот угол входит и в прямоугольный треугольник который строят для определения НВ отрезка (Рис.3.8.). Таким образом, угол между катетом - проекцией и гипотенузой прямоугольного треугольника равен истинной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения.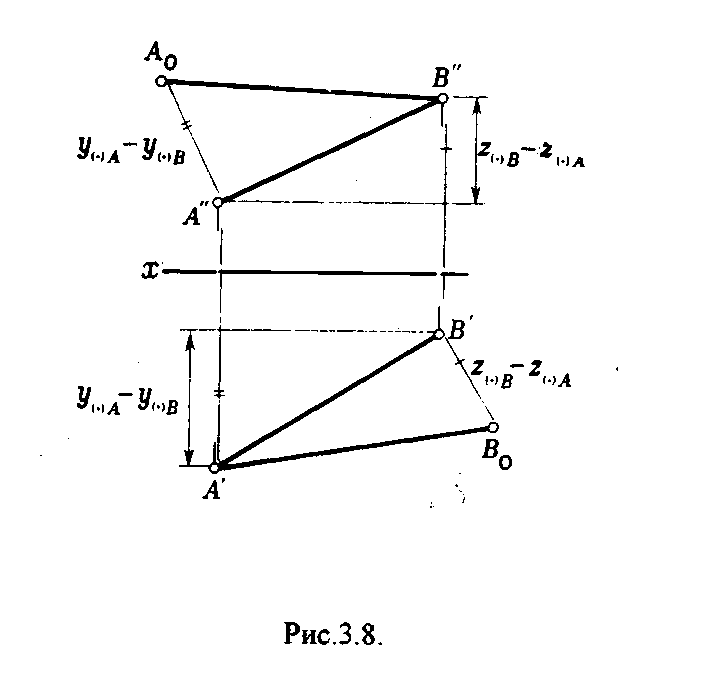


Рис.3.8.

4. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ

4.1. Способы задания плоскости на чертеже

На чертеже плоскость может быть задана следующими способами:

- проекциями трех точек, не принадлежащими одной прямой;

- проекциями прямой и не принадлежащей ей точки;

- проекциями пересекающихся прямых;

- проекциями параллельных прямых;

- проекциями плоской геометрической фигуры;

- следами.