Конспект объясняющего модуля
 Скачать 35.14 Kb. Скачать 35.14 Kb.
|
|
Конспект объясняющего модуля Связь между координатами вектора и координатами его начала и конца Метод координат позволяет изучать геометрические фигуры и их свойства с помощью уравнений и неравенств. Одним из основных понятий этого метода является понятие координат вектора. Покажем связь между координатами вектора и координатами его начала и конца. 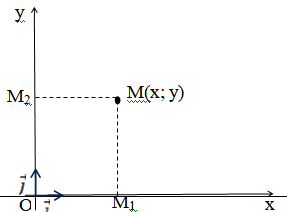 Рассмотрим прямоугольную систему координат и какую-нибудь точку М с координатами x и y. Чтобы определить числа x и y, проведём через точку М прямые, перпендикулярные к осям координат, и обозначим через M1 и M2 точки пересечения этих прямых с осями Оx и Оy . Число x – абсцисса точки М, равно отрезку ОМ1, если M1 – точка положительной полуоси: х = ОМ1. Если точка M1 – точка отрицательной полуоси, то х = –ОМ1. Если точка M1 совпадает с точкой О, то икс в этом случае равен нулю. Аналогично определяется число y – ордината точки M2. Докажем, что координаты точки М равны соответствующим координатам её радиус-вектора. 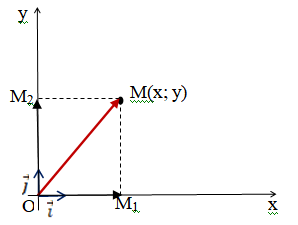 Радиус-вектор точки М – это вектор, соединяющий начало координат и точку М. 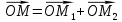 Докажем следующие равенства 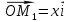 и и 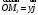 Действительно, 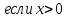 , то , то 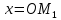 , , 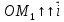 и справедливо равенство: и справедливо равенство: 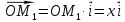 Если x < 0, то 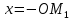 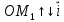 и справедливо следующее равенство: и справедливо следующее равенство: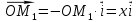 Наконец, если 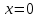 , то , то 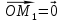 и равенство в этом случает также справедливо: и равенство в этом случает также справедливо: 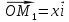 Таким образом, в любом случае равенство справедливо. Аналогично доказывается и второе равенство 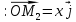 Следовательно, 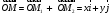 А это значит, что координаты радиус вектора OM равны соответствующим координатам точки M: 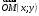 Пользуясь доказанным утверждением можно выразить координаты любого вектора через координаты его начала и конца. |
