шпора термех. Равнодействующая системы параллельных сил равна
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
      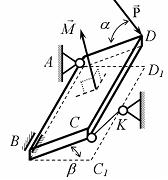 Для пространственной конструкции в точке А связью является сферический шарнир. Такое закрепление ограничивает для точки А плиты все три линейных перемещения по осям координат и разрешает вращения вокруг трех взаимно перпендикулярных осей. Поэтому реакция в точке А имеет три составляющие – или проекции реакции связи на три взаимно перпендикулярные оси (например, ХА, YА, ZA). Ответ: 3. Для пространственной конструкции в точке А связью является сферический шарнир. Такое закрепление ограничивает для точки А плиты все три линейных перемещения по осям координат и разрешает вращения вокруг трех взаимно перпендикулярных осей. Поэтому реакция в точке А имеет три составляющие – или проекции реакции связи на три взаимно перпендикулярные оси (например, ХА, YА, ZA). Ответ: 3. Перпендикулярно к отрезку МN приложены две параллельные силы: F = 4 H и T = 6 H. |MN| = 3 м. Укажите модуль и точку приложения равнодействующей т. С. Перпендикулярно к отрезку МN приложены две параллельные силы: F = 4 H и T = 6 H. |MN| = 3 м. Укажите модуль и точку приложения равнодействующей т. С.Равнодействующая системы параллельных сил равна Центр приложения равнодействующей системы параллельных сил находится как 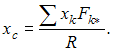 Относительно точки М: Относительно точки М: Ответ: R = 10 Н, |МС| = 1,8 м. 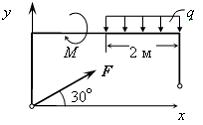 На раму действуют сосредоточенная сила F величиной 15 кH, пара сил с моментом М = 4 кН·м, равномерно распределенная на участке сила интенсивностью q = 3 кН/м. Главный вектор данной системы сил равен ___ кН. На раму действуют сосредоточенная сила F величиной 15 кH, пара сил с моментом М = 4 кН·м, равномерно распределенная на участке сила интенсивностью q = 3 кН/м. Главный вектор данной системы сил равен ___ кН.Главный вектор системы сил равен Проекции главного вектора на оси координат равны Модуль главного вектора плоской системы сил 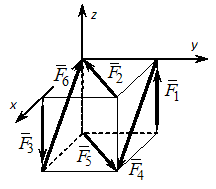 По граням и ребрам куба действуют 6 равных по модулю сил Главный вектор системы сил (геометрическая сумма всех сил) по модулю равен … По граням и ребрам куба действуют 6 равных по модулю сил Главный вектор системы сил (геометрическая сумма всех сил) по модулю равен …Главный вектор системы сил равен Проекции и модуль главного вектора системы сил равны: Силы и и и образуют пары сил и при сложении они попарно сокращаются. Поэтому главный вектор равен 0. 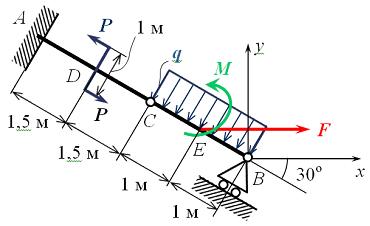 Однородная невесомая балка АВ длиной 5 м концом А закреплена при помощи жесткой заделки, в точке B прикреплена к шарнирно-подвижной опоре. В точке С расположен промежуточный цилиндрический шарнир. На балку действуют: сосредоточенная горизонтальная сила F = 1 H, равномерно распределенная нагрузка интенсивности q = 5 Н/м, момент М = 4 Нм, пара сил с Р = 3 Н и плечом 1 м. Однородная невесомая балка АВ длиной 5 м концом А закреплена при помощи жесткой заделки, в точке B прикреплена к шарнирно-подвижной опоре. В точке С расположен промежуточный цилиндрический шарнир. На балку действуют: сосредоточенная горизонтальная сила F = 1 H, равномерно распределенная нагрузка интенсивности q = 5 Н/м, момент М = 4 Нм, пара сил с Р = 3 Н и плечом 1 м.Момент силы F относительно центра С Алгебраический момент силы F относительно центра С равен 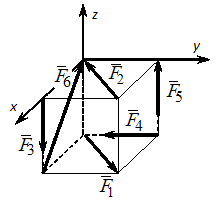 По граням и ребрам куба действуют 6 равных по модулю сил Ребро куба равно а. Момент силы относительно оси y равен … По граням и ребрам куба действуют 6 равных по модулю сил Ребро куба равно а. Момент силы относительно оси y равен …Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную к оси, и вычисленному относительно точки пересечения оси с плоскостью. При этом алгебраический момент силы относительно какой-либо точки равен взятому со знаком плюс либо минус произведению модуля силы на кратчайшее расстояние от этой точки до линии действия силы (плечо силы относительно этой точки). Момент силы относительно оси принято считать положительным, если сила стремится вращать тело вокруг оси против хода часовой стрелки, если смотреть с положительной стороны оси. В данном случае 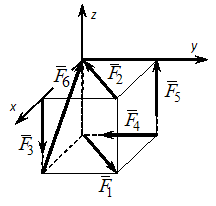 По граням и ребрам куба действуют 6 равных по модулю сил . Ребро куба равно а. Модуль главного момента данной системы сил относительно начала координат По граням и ребрам куба действуют 6 равных по модулю сил . Ребро куба равно а. Модуль главного момента данной системы сил относительно начала координат Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную к оси, и вычисленному относительно точки пересечения оси с плоскостью. При этом алгебраический момент силы относительно какой-либо точки равен взятому со знаком плюс либо минус произведению модуля силы на кратчайшее расстояние от этой точки до линии действия силы (плечо силы относительно этой точки). Главный момент системы сил относительно начала координат т. О равен Проекции главного момента системы сил (или суммы моментов сил относительно осей координат) равны: Модуль главного момента 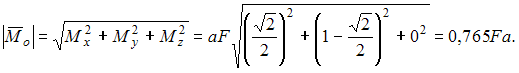  Данную систему сил можно привести в центре О к векторам и (см. рис.). Если и не перпендикулярен (где  главный вектор системы сил; главный вектор системы сил;  главный момент системы сил относительно начала координат точки О), то данная система сил … главный момент системы сил относительно начала координат точки О), то данная система сил …В случае, когда и не перпендикулярен система приводится к динамическому винту. Статически определимы системы … Для твердого тела под действием произвольной плоской системы сил можно составить три независимых уравнения равновесия. Если конструкция состоит из нескольких тел, такие уравнения можно составить для всех тел. Промежуточный шарнир также позволяет составить еще одно независимое уравнение равновесия. Если число неизвестных реакций совпадает с числом независимых уравнений равновесия – система статически определима.  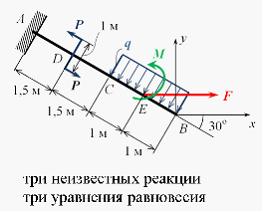 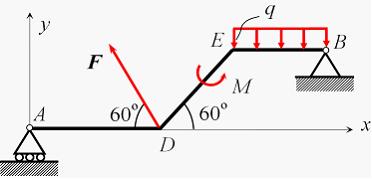 На раму ADEB действуют: сосредоточенная сила F величиной 25 кH, пара сил с моментом М = 5 кН·м, равномерно распределенная на участке EВ сила интенсивностью q = 2 кН/м. Длины участков AD, DE и EВ равны 2 м. Модуль реакции опоры в точке А равен ___ кН. (Полученный ответ округлите с точностью до десятых.) На раму ADEB действуют: сосредоточенная сила F величиной 25 кH, пара сил с моментом М = 5 кН·м, равномерно распределенная на участке EВ сила интенсивностью q = 2 кН/м. Длины участков AD, DE и EВ равны 2 м. Модуль реакции опоры в точке А равен ___ кН. (Полученный ответ округлите с точностью до десятых.)Для плоской произвольной системы сил можно составить три независимых условия (уравнения) равновесия: 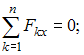 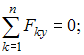 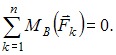 Рама в точке А прикреплена к шарнирно-подвижной опоре, в точке В – к шарнирно-неподвижной опоре. Поэтому полная реакция в точке В имеет две взаимно-перпендикулярные составляющие реакции и , в точке А – одну . 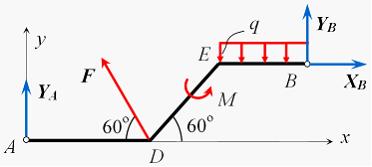 Из уравнения равновесия моментов относительно точки В находим 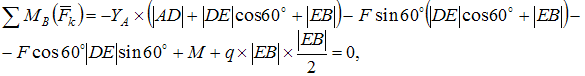 Откуда 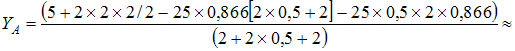 №11  Прямоугольная плита весом G = 15 кН удерживается в горизонтальном положении сферическим шарниром О, подшипником А и тросом BE, причем точки О и Е находятся на одной вертикали. Прямоугольная плита весом G = 15 кН удерживается в горизонтальном положении сферическим шарниром О, подшипником А и тросом BE, причем точки О и Е находятся на одной вертикали.В точке D к плите приложена сила Р = 5 кН, перпендикулярная к стороне OD и наклоненная к плоскости плиты под углом 45°. α = β = 30° и |ОА| = 2|OD|. Вертикальная составляющая реакции в опоре A по модулю равна ____ (кН). (Полученный ответ округлите с точностью до десятых.)  Рассмотрим равновесие плиты. Реализуем принцип освобождаемости от связей, согласно которому к активным силам P и G добавим реакции связей. Можно составить 6 условий равновесия пространственной произвольной системы сил:   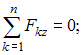 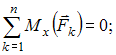 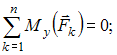 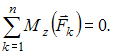 Из условия равновесия моментов относительно прямой ОВ 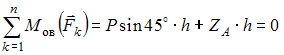 находим реакцию находим реакцию 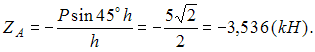 Здесь h – расстояния от точек D и А до прямой ОВ. Здесь h – расстояния от точек D и А до прямой ОВ.12 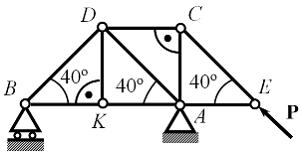 В ферме не нагружены стержни … В ферме не нагружены стержни …Для решения воспользуемся способом «вырезания» узлов. «Вырежем» узел K. Действие отброшенных связей на узел K заменим реакциями или усилиями в стержнях SBK, SKA и SDK. 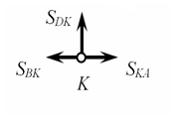 Рассмотрим равновесие узла K. Для получившейся плоской системы сходящихся сил можно составить два уравнения равновесия:   Поскольку вертикальная сила одна – SDK, она будет равна 0. Ненагруженным является стержень DK. Поскольку вертикальная сила одна – SDK, она будет равна 0. Ненагруженным является стержень DK.Рассуждая аналогично, вырежем узел Е, спроектируем силы в узле Е на прямую СЕ и перпендикуляр к ней. На перпендикуляр к прямой СЕ проекцию имеет только усилие SАЕ, поэтому оно будет равно 0. Стержень АЕ также является ненагруженным.  На плоскую ферму (см. рис.) в узле К действует сила На плоскую ферму (см. рис.) в узле К действует сила Согласно способу Риттера, каждая неизвестная сила должна быть определена из отдельного уравнения равновесия и не должна выражаться через реакции других стержней. Для определения реакции S6мысленно разрежем ферму сечением I-I.  Рассматриваем равновесие сил, приложенных к верхней части фермы. Действие отброшенной нижней части на верхнюю представлено силами S6,S7 и S8. Условно предполагаем все стержни растянутыми. Знак минус в ответе укажет на то, что соответствующий стержень испытывает сжатие. Для определения величины S6 составим уравнение моментов сил относительно точки К (точки Риттера для стержня 6), где пересекаются линии действия векторов S7 и S8: Получим S6 = 0. 14 Для представленной фигуры наиболее близко к центру тяжести расположена точка …  Наличие прямоугольного выреза смещает центр тяжести в противоположную сторону от общей вертикальной оси симметрии треугольника и квадратов. Точки 1 и 2 лежат на этой общей оси, поэтому отпадают. Прямоугольный вырез и треугольник смещают центр тяжести вверх относительно горизонтальной оси симметрии квадратов. Точка 4 слишком близка к этой горизонтальной оси. Правильный ответ – точка 3. Наличие прямоугольного выреза смещает центр тяжести в противоположную сторону от общей вертикальной оси симметрии треугольника и квадратов. Точки 1 и 2 лежат на этой общей оси, поэтому отпадают. Прямоугольный вырез и треугольник смещают центр тяжести вверх относительно горизонтальной оси симметрии квадратов. Точка 4 слишком близка к этой горизонтальной оси. Правильный ответ – точка 3.15.  На наклонной плоскости под действием приложенных сил покоится цилиндрический каток. Радиус катка – 0,5 м, масса катка – 100 кг, коэффициент трения скольжения f – 0,15, коэффициент трения качения Рассмотрим цилиндрический каток, покоящийся на наклонной плоскости. В покое для плоской системы сил: веса катка нормальной реакции опоры силы трения покоя (скольжения) приложенной силы момента трения качения МС – должны удовлетворяться все три условия равновесия: Уравнение моментов относительно точки О имеет вид: S·R – P·R·sin 5° – МС = 0, если предельное равновесие при движении вверх (как на рисунке); S·R – P·R·sin 5° + МС = 0, если предельное равновесие при движении вниз (момент трения направлен по часовой стрелке). Из этого уравнения следует, что пока качения нет, момент трения равен ± МС = S |
