шпора термех. Равнодействующая системы параллельных сил равна
 Скачать 1.02 Mb.
|
·R – P·R·sin 5°.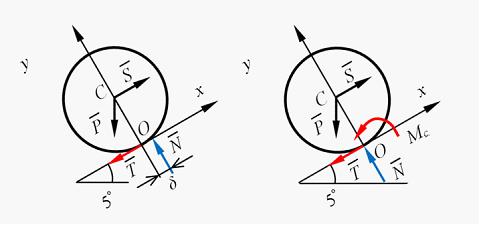 Постепенно увеличивая (уменьшая) силу S, можно прийти к такому предельному состоянию равновесия, когда малейшее приращение силы Sвызывает качение катка по опоре. В этом состоянии предельного равновесия момент трения качения принимает свое наибольшее по модулю значение  где  Момент трения качения, таким образом, изменяется в пределах  Окончательно для сохранения покоя катка получаем: 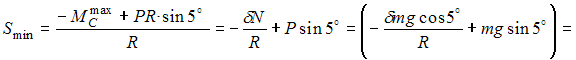 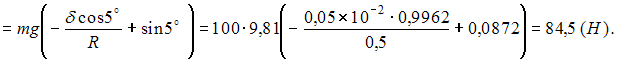 16. Движение задано векторным способом Тогда в момент времени проекция скорости на ось OX равна ______ м/с. Перейдем к координатному способу задания движения. Коэффициенты при ортах равны координатам x и yсоответственно:  17. Движение задано координатным способом; где x и y в метрах. При скорость материальной точки по модулю равна ____ м/с.  при   18. Касательное ускорение точки при ее криволинейном движении характеризует изменение … Касательное ускорение точки при ее криволинейном движении характеризует изменение скорости по величине. 19. 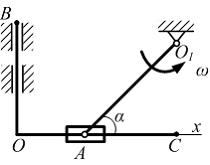 В кривошипно-кулисном механизме, кривошип ОAвращается по закону Ползун А, перемещаясь вдоль ОС, приводит в движение кулису ВОС. Если  то скорость точки В кулисы равна ____  Рассмотрим движение точки А как сложное движение. По теореме о сложении скоростей при сложном движении, абсолютная скорость точки Aравна: Точка А принадлежит кривошипу ОА, который вращается с угловой скоростью.  и  и С кулисой BOC свяжем подвижную систему координат xoy. Она движется поступательно. Следовательно, переносная скорость ползуна A равна и направлена по вертикальной прямой. Относительная скорость направлена вдоль ОС. Построим параллелограмм скоростей. Решаем прямоугольный треугольник  20.  Клин скользит по горизонтальной плоскости, так, что расстояние Вдоль наклонной плоскости движется точка M по закону Ускорение Кориолиса точки при равно _____ Ускорение Кориолиса определяется по формуле (удвоенное векторное произведение). Переносное движение точки M – движение подвижной системы (движение клина) поступательное. Поэтому переносная угловая скорость и Ответ 0. 21.  Пластина радиуса R = 0,25 м вращается вокруг оси Oz, перпендикулярной плоскости чертежа, по закону Вдоль диаметра с постоянной скоростью движется точка М. Абсолютное ускорение точки M в момент прохождения через центр окружности т. С равно ____  По теореме Кориолиса  Переносное движение – вращательное, по закону    Вектор угловой скорости направлен по оси вращения (см. рисунок). направлено к оси вращения. Относительное движение − равномерное, прямолинейное.  Ускорение Кориолиса Угол между прямой.  Направление находим по правилу Жуковского: спроектируем на плоскость, оси Oz и повернем эту проекцию на в сторону вращения. Получим направление Складываем 2 вектора, направленные в противоположные стороны. Модуль суммы этих векторов равен разности модулей  и направлен в сторону вектора с большим модулем.Ответ: 22. Рассмотрим различные виды движений, в которых может участвовать несвободное твердое тело: (1) сферическое; (2) поступательное; (3) плоскопараллельное. Установите соответствие между видом движения и его особенностью. Сферическим называется такое движения твердого тела, при котором во время движения одна и та же точка тела остается неподвижной. Плоскопараллельным (плоским) называется такое движение твердого тела, при котором все точки тела перемещаются в плоскостях, параллельных некоторой заданной неподвижной плоскости (основной плоскости). Поступательным называется такое движение твердого тела, когда всякая прямая, мысленно проведенная в теле, перемещается параллельно самой себе. Движение тела называется вращательным, если, по крайней мере, две точки тела являются неподвижными. 23.  По диагонали квадратной пластины, скользящей вдоль горизонтальных направляющих со скоростью v1 = 2 м/с, двигается параллелепипед со скоростью v2 = 3 м/с. Абсолютная скорость параллелепипеда по модулю равна ___ м/с. Относительное движение параллелепипеда (движение относительно пластины) является поступательным. Переносное движение пластины также является поступательным. Поэтому абсолютное движение параллелепипеда будет также поступательным. Согласно теореме о сложении скоростей или  24.  Механизм состоит из однородного шкива 1 и ступенчатого шкива 2.   Шкив 1 вращается по закону  Проскальзывания между шкивами не происходит. Ускорение точки А шкива 2 в момент времени равно _____ Точка К принадлежит к обоим шкивам. Поэтому отсюда    при     25.  Шкив 1 (см. рис.), вращаясь по закону  передает вращение на шкив 2 с помощью цепной передачи Если проскальзывание цепи не происходит и то угловое ускорение шкива 2 равно ___ рад/с2.Участок цепи BD (или CE) движется поступательно. Следовательно, Отсюда и   26.  Мгновенный центр скоростей стержня AE находится в точке …  Представлен плоский механизм. Стержень AGвращается вокруг неподвижной т. G, поэтому скорость т. А направлена перпендикулярно стрежню AG. Стержень EH вращается вокруг неподвижной т. H, поэтому скорость т. E направлена перпендикулярно стрежню EH. Точки A и E принадлежат стержню AE.На пересечении перпендикуляров к скоростям точек Aи E находится МЦС стрежня AE – т. K. 27.  Кривошип OA кривошипно-шатунного механизма вращается с угловой скоростью  Если уголBOA – прямой, OA = 0,5 м, то угловая скорость шатунаAB равна ___  Скорость точки A кривошипа, ОА. Шатун АВсовершает плоское движение. Ползун B совершает прямолинейное движение и направлена вдоль ОВ. Мгновенный центр скоростей для АВ находится на пересечении перпендикуляров к то есть находится в бесконечности. Это случай мгновенного поступательного движения и 28. Стержень АВ длиной 3 м двигается в плоскости чертежа с угловой скоростью w = 1 рад/с и угловым ускорениемe = 1,5 рад/с2. Ускорение т. А . Тогда ускорение т. В будет равно _____ м/с2.  Запишем для стержня АВ уравнение метода полюсов, приняв за полюс т. А:  .Здесь  центростремительное и вращательное ускорения т. В при ее вращении вокруг полюса А:  направлено от т. В. к т. А. Спроецируем уравнение метода полюсов на горизонтальную и вертикальную оси. В результате получим   Окончательно получим  29.  Тело двигается плоскопараллельно с угловой скоростьюw и угловым ускорением e. Точка А имеет ускорение  .Точка В –  Если АВ равно 2 м, то угловое ускорение тела равно _____ с-2.  Запишем для стержня АВ уравнение метода полюсов, приняв за полюс т. А: .Здесь центростремительное и вращательное ускорения т. В при ее вращении вокруг полюса А: направлено от т. В к т. А. Спроецируем уравнение метода полюсов на горизонтальную и вертикальную оси. В результате получим  ;  .Окончательно получим  30.  Подвижный конус А двигается с мгновенной угловой скоростью ω.Угловая скорость конуса А при качении без проскальзывания по неподвижному конусу В равна …  Произвольно выбранная на оси симметрии конуса Аточка К поворачиваетсявместе с конусом А вокруг оси Оу конуса В с угловой скоростью ωl. В тоже время, конус А (и т. К соответственно тоже) совершает мгновенный поворот вокруг мгновенной оси вращения Оh с мгновенной угловой скоростьюω. Для этих двух поворотов скорость т. К можно найти как  где DK ^ Оу и KC ^ Оh – расстояния от точки до осей Оу и Оh,   Окончательно  31.  Подвижный конус B катится по неподвижному конусу Aбез проскальзывания, имея неподвижную точку О (см. рис.). Мгновенной осью вращения конуса В будет ось … Мгновенной осью вращения будет ось, на которой лежат неподвижные в данный момент точки подвижного конуса В. Такой осью будет ось Ох. 32.  Подвижный конус А катится по неподвижному конусу Вбезпроскальзывания (см. рис.).Мгновенная угловая скорость направлена вдоль оси … Мгновенная угловая скорость всегда направлена вдоль мгновенной оси вращения. Мгновенной осью вращения будет ось, на которой лежат неподвижные в данный момент точки подвижного конуса А. Такой осью будет ось Оh. 33. Дифференциальное уравнение свободных колебаний при отсутствии сопротивления имеет вид … Дифференциальное уравнение свободных колебаний при отсутствии сопротивления имеет вид  34. Количество движения материальной точки не изменяется за промежуток времени, если … Количество движения материальной точки не изменяется за промежуток времени, если импульс силы за этот же промежуток времени будет равным нулю. 35. Вектор момента количества движения материальной точки относительно оси остается постоянным при условии … Вектор момента количества движения материальной точки относительно оси остается постоянным при условии равенства нулю относительно выбранной оси момента силы, приложенной к материальной точке. 36. Из горизонтально расположенного ствола орудия длиной 3 м со скоростью 700 м/с вылетает снаряд массой 25 кг. Среднее значение силы давления газов на снаряд равно ___ кН. Согласно теореме об изменении кинетической энергии, mv12/2 – mv02/2 = Рср×lствола. Так как v0 = 0, то Рср = mv12/(2lствола) = 25 7002/6 = 2042 кН. 37. При движении автомобиля на него действует сила сопротивления воздуха F=Схpv2S/2, где плотность воздуха p = 1 кг/м3; коэффициент лобового сопротивления Сх = 0,3; площадь проекции автомобиля на плоскость, перпендикулярную направлению движения, S = 3 м2. На скорости v = 90 км/ч величина мощности, необходимой на преодоление сопротивления воздуха, равна ___ кВт. Скорость автомобиля в системе СИ v = 25 м/с. Сила сопротивления воздухаF = Сх p v2 S/2 = 0,3∙1∙252∙3/2 = 281 Н. Мощность, необходимая на преодоление сопротивления воздуха N = Fv = 281∙25 = 7025 Вт = 7,025 кВт. 38. Груз Р совершает колебания на системе из двух параллельных пружин, жесткости которых равны и соответственно. Одна пружина, эквивалентная данной системе пружин, имеет жесткость ___ Н/см. При параллельном соединении пружин  39. Лифт опускается с ускорением а. Сила давления груза массой m на дно лифта равна … Согласно принципу Даламбера для материальной точки, G + N + Ф = 0, где G = mg – вес груза; N – реакция пола лифта; Ф – сила инерции. Проецируя все силы на вертикальную ось, получим G – N – Ф = 0, или N = G – Ф = mg – mа. 40.  Момент инерции сплошного однородного диска массойm относительно оси, проходящей через т. О(перпендикулярно плоскости диска), равен ____ . Момент инерции сплошного однородного диска массойm относительно оси, проходящей перпендикулярно плоскости диска через центр тяжести,  Согласно теореме Гюйгенса-Штейнера, для параллельных осей  Окончательно  .41.  На однородную гладкую призму A (см. рис.), лежащую на гладкой горизонтальной плоскости, положена однородная гладкая призма B. Призмы в поперечном сечении являются прямоугольными треугольниками. Масса призмы A вдвое больше массы призмы B. Если призма B спустится по призме A до горизонтальной плоскости, призма A переместится на расстояние, равное …  Согласно закону сохранения движения центра масс, если сумма проекций внешних сил системы на некоторую неподвижную ось равна нулю, то проекция вектора скорости центра масс на эту ось остается постоянной. Внешние силы – сила тяжести и нормальная реакция вертикальны, то есть скорость центра масс системы в проекции на ось х постоянна. Так как в начальный момент времени призмы находились в покое, эта проекция скорости равна 0. Следовательно, по оси х центр масс системы не перемещается. Центр масс системы определяется как   В начальный момент времени  Тогда  В конечный момент времени   Тогда  Учтя, что получим  Окончательно 42.  Механическая система состоит из катка 1 и блоков 2 и 3, соединенных невесомой нерастяжимой нитью (см. рис.). Массы катка блока 2 и блока 3 Радиус катка – 0,5 м. Каток катится по горизонтальной поверхности с угловой скоростью Количество движения системы равно ___ кг×м/с.  Количество движения системы  или в проекциях    Скорость центра масс катка  Количество движения катка  Скорость центра масс блока 2 равна 0, следовательно, Скорость центра масс блока 3  Количество движения блока 3  Окончательно  43.  Груз 1 с массой приводит в движение однородный блок 2 с массой с радиусом Ускорение свободного падения считать равным 10 м/с2. Угловая скорость блока через равна ____ рад/с. Для решения задачи применим теорему об изменении кинетического момента системы относительно оси вращения О.  Здесь кинетический момент системы равен сумме кинетических моментов тел системы  где     Сумма моментов внешних сил равна:  Подставим выражение (2) в (1).    Получили дифференциальное уравнение.Интегрируем   44.  Механическая система состоит из однородного колеса 1 массой радиуса и однородного стержня 2, массы длиной соединенных шарниром А. Изменение кинетической энергии МС за время перехода из положения I, в положение II составит ____ Дж. (Силы трения не учитывать.) Изменение кинетической энергии МС на конечном участке пути равно сумме работ внешних сил на этом пути. Работа внутренних сил для твердых тел равна нулю.    45. Формальное математическое описание связи, наложенной на материальную точку М(x, y, z), имеет вид Данная связь является … Формальное математическое описание данной связи содержит производные от координат (то есть скорости) и знак равенства, поэтому данная связь является кинематической и неосвобождающей. В уравнение связи не входит время t в явном виде, поэтому связь является стационарной. Уравнение связи легко интегрируется и преобразуется к соотношению между координатами, поэтому связь является голономной. 46. Механическая система состоит из двух материальных точек А и В, связанных между собой жестким невесомым стержнем. Число обобщенных координат, определяющих положение такой системы (число степеней свободы), равно … Пространственное положение каждой из двух точек определяется тремя декартовыми координатами. Но эти шесть параметров связаны одним соотношением – условием постоянства расстояния между точками. Поэтому число независимых параметров 6 – 1 = 5. Это и есть число степеней свободы системы и одновременно число ее обобщенных координат. 47. Механическая система состоит из двух материальных точек, которые связаны невесомой пружиной и могут перемещаться только в одной неподвижной плоскости. Число уравнений Лагранжа для такой системы равно … Упругая связь между точками не накладывает никаких ограничений на их положения на плоскости. Поэтому каждая точка обладает двумя степенями свободы, а механическая система, которую они составляют, имеет четыре степени свободы. Положение такой системы можно описать четырьмя обобщенными координатами. Число уравнений Лагранжа для такой системы также равно 4. 48.  Геометрические размеры  (см. рис.).Соотношение dj2/dj1 между возможными поворотами тел СВ и АС равно …В т. А стержень АС прикреплен к шарнирно-неподвижной опоре. Следовательно, для стержня АСвозможным перемещением, согласованным с наложенными связями, будет возможный поворот наdj1вокруг т. А – центра вращения стержня АС. При определении реакции ХB в т. В коленчатый стержень ВС прикреплен к шарнирно-подвижной опоре. Возможным перемещением т. В будет перемещение по горизонтали.  Стержни АС и ВС шарнирно соединены в т. С. Тогда получаем, что т. O – мгновенный центр вращения стержня ВС. Стержень ВС совершает возможный поворот вокруг т. О на угол dj2. Возможное перемещение т. С:  где  Тогда  и окончательно  49.  Общим уравнением динамики, выражающим Принцип Даламбера – Лагранжа, является … Согласно Принципу Даламбера – Лагранжа, при любом движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы равна нулю. Общее уравнение динамики имеет вид  50. Рассматривается процесс ударного взаимодействия двух тел: тело 1 до удара движется, а тело 2 − неподвижно. |