шпора термех. Равнодействующая системы параллельных сил равна
 Скачать 1.02 Mb.
|
|
Неверным является следующее утверждение … Утверждение, что импульсы ударной силы, действующей на тело 1, в первой фазе удара и во второй фазе удара одинаковы по величине неверно. Импульсы будут одинаковы только в том случае, если удар – абсолютно-упругий. 51. Удару соответствуют временные зависимости количества движения таких систем, как … Количество движения механической системы при ударе изменяется мгновенным скачком, равным геометрической сумме внешних ударных импульсов. 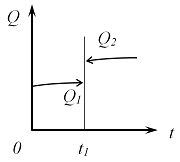 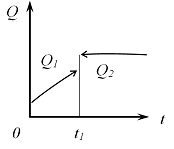 52. 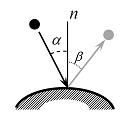 Материальная точка ударяется о неподвижное основание и отскакивает (см. рис.). Скорость точки до удара равна 5 м/с и образует с нормалью к поверхности угол = 36°52' (угол падения). Скорость точки после удара равна 4 м/с. Коэффициент k восстановления при ударе равен 0,3. Трением пренебрегаем. Угол отражения после удара равен … 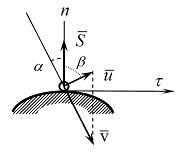 Если до удара скорость центра масс тела равна v, после удара – u, то теорема об изменении количества движения системы в проекциях на нормаль и касательную будет иметь вид 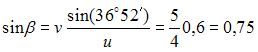  Тогд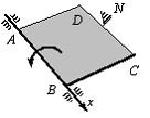а и  откуда  и 53.  Вращаясь вокруг оси Ах с угловой скоростью 6 рад/с, квадратная пластина ABCD наталкивается на неподвижное препятствие в точке N и после удара останавливается (см. рис.). Масса пластины 20 кг, длина стороны АВ = ВC = 0,5 м. Момент импульса ударной реакции в точке Nотносительно оси Ах по модулю равен ____ Нсм. Момент инерции пластины относительно оси Ах равен 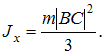 Кинетический момент системы в начальный момент времени равенПосле удара  Теорема об изменении кинетического момента системы при ударе  Тогда момент импульса ударной реакции в точке Nравен 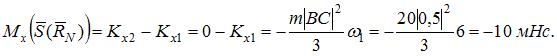 54. 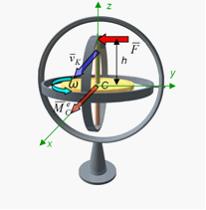 Второе свойство гироскопа: … Второе свойство гироскопа: при действии силы (или пары сил) на ось быстро вращающегося гироскопа она будет отклоняться не в сторону действия силы, как это было бы при невращающемся роторе, а в направлении, перпендикулярном этой силе. Данное свойство наблюдается как у астатического, так и тяжелого гироскопа. 55. 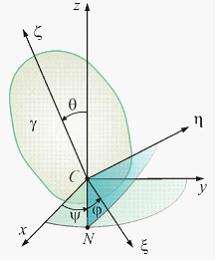 Пусть даны неподвижные Сх, Су и Сz и подвижные оси Ch, Cx и Cz (главные центральные оси инерции вращающегося вокруг т.С твердого тела), – орты подвижной системы координат Ch, Cx и Cz.Примем: – проекция главного момента внешних сил на ось l, – осевой момент инерции тела, –кинетический момент тела, – угловая скорость тела относительно некоторой оси l.Обозначим углы Эйлера: j − угол вращения, q − угол нутации, y − угол прецессии. Тогда формулы Пуассона будут … Поскольку производная от вектора постоянной длины равна векторному произведению угловой скорости на сам вектор, формулы Пуассона получаются в виде  56. 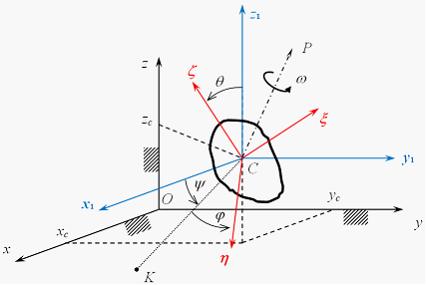 Оси Ох, Оу и Оz являются неподвижными осями координат; оси Ch, Cx и Cz – главными осями инерции твердого тела, оси Cx1, Cy1 и Cz1 – осями Кенига (см. рис.). Пусть СК – линия узлов, т. С – полюс. Тогда уравнения движения свободного твердого тела включают в себя … Элементарное движение свободного твердого тела складывается из поступательного вместе с полюсом С:  и и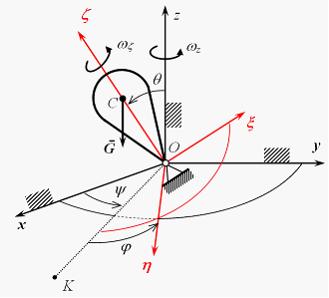з некоторого перемещения по отношению к осям Кенига Cx1, Cy1 иCz1 (вращения вокруг т. С как неподвижной)  57.  Гироскоп (см. рис.) весом G = 10 Н вращается с угловой скоростью  вокруг оси Оz, проходящей через центр масс С и неподвижную точку О. Угол нутации постоянен по величине, момент инерции относительно оси симметрии  Угловая скорость установившейся прецессии Расстояние ОС равно ____ м.По теореме Резаля скорость конца вектора кинетического момента механической системы относительно некоторого неподвижного центра Огеометрически равна главному моменту внешних сил, действующих на эту систему, относительно того же центра: То есть действие постоянной внешней силы на ось гироскопа приводит к повороту этой оси с некоторой угловой скоростью (остальные внешние силы – реакции связей приложены к неподвижной точке О). По формуле Эйлера для скорости получаем С учетом равенства из теоремы Резаля находим  или  гдеq − угол нутации. Ось гироскопа при этом описывает коническую поверхность. Такое движение (поворот вокруг оси Оz) называется прецессией, угловая скорость прецессии. Момент внешних сил  Окончательно получаем 58.  Для приведенного графика движения упругой колебательной системы с одной степенью свободы (q – обобщенная координата, t – время, начальные условия , ) дифференциальное уравнение движения имеет вид … Указанный график соответствует свободным колебаниям системы при наличии линейного сопротивления. Дифференциальное уравнение таких затухающих колебаний имеет вид  59.  Механическая система совершает колебания (см. рис.), описываемые законом  , (см), где q – обобщенная координата, t – время, начальные условия:, . Дифференциальное уравнение движения этой системы и начальные условия колебаний имеют вид …Представлен график и закон свободных колебаний вида  . Дифференциальное уравнение свободных колебаний имеет вид где угловая частота свободных колебаний системы, с – жесткость упругого элемента, m – масса. Амплитуда колебаний  начальная фаза колебаний  Тогда   60.  Консервативная механическая система с одной степенью свободы имеет устойчивое положение равновесия при значении обобщенной координаты В положении равновесия значение потенциальной энергии Тогда функция, определяющая потенциальную энергию, может иметь вид … Необходимое условие равновесия системы с одной степенью свободы  Достаточные условия устойчивости положений равновесия для консервативных систем определяются теоремой Лагранжа – Дирихле: положение равновесия консервативной механической системы устойчиво, если в положении равновесия потенциальная энергия системы имеет изолированный минимум.Потенциальная энергия механической системы определяется с точностью до постоянной. Выберем эту постоянную так, чтобы в положении равновесия потенциальная энергия равнялась нулю П(0) = 0. Тогда для системы с одной степенью свободы достаточным условием существования изолированного минимума будет условие  Рассмотрим выражение  Для него  и   Ответ: 61.  Механическая система (см. рис.) состоит из невесомой трубки, имеющей в т. О горизонтальную ось вращения, и шарика массой m, который перемещается по трубке без трения и связан с точкой O трубки пружиной. Пусть длина недеформированной пружины а, жесткость пружины c. Координата х положения шарика на трубке отсчитывается от т. О, угол j – от вертикальной оси.Устойчивым будет равновесие при … Если механическая система находится в равновесии в потенциальном силовом поле, то из уравнений Лагранжа 2-го рода получаем необходимые условия равновесия:  , j =1, 2, …, s, где qj – j-ая обобщенная координата; s– число обобщенных координат в механической системе.Следовательно, в положении равновесия потенциальная энергия имеет экстремальное значение. Не всякое равновесие может быть реализовано практически. В зависимости от поведения системы при отклонении от положения равновесия говорят об устойчивости или неустойчивости данного положения. Достаточные условия устойчивости положений равновесия для таких систем определяются теоремой Лагранжа – Дирихле:положение равновесия консервативной механической системы устойчиво, если в положении равновесия потенциальная энергия системы имеет изолированный минимум. Для системы с двумя степенями свободы достаточными условиями существования изолированного минимума будут, согласно критериям Сильвестра, неравенства  и  Потенциальная энергия системы  Пусть Тогда    Условиям   и  соответствует положение равновесия при  62. |