Площадь сечений. Задача Найдите площадь сечения куба abcda1B1C1D1 плоскостью, проходящей через середины рёбер ab, ad и cc1, если его сторона равна Задача 2
 Скачать 24.33 Kb. Скачать 24.33 Kb.
|
|
Площадь сечений Теорема о площади ортогональной проекции. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции, т. е. 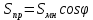 . .Задача 1. Найдите площадь сечения куба ABCDA1B1C1D1 плоскостью, проходящей через середины рёбер AB, AD и CC1, если его сторона равна 1. Задача 2. Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α содержащей прямую BD1 и параллельной прямой AC, является ромб. а) Докажите, что грань ABCD – квадрат. б) Найдите угол между плоскостями α и BCC1, если AA1 = 6, AB = 4. Задача 3. Плоскость α перпендикулярна основанию правильной треугольной пирамиды SABC и делит стороны AB и BC основания пополам. а) Докажите, что плоскость α делит боковое ребро в отношении 1 : 3, считая от вершины S. б) Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна 2, а высота пирамиды равна 4. Задача 4. Дана треугольная призма ABCA1B1C1. Плоскость α проходит через прямую BC1 параллельно прямой AB1. а) Докажите, что плоскость α проходит через середину ребра AC. б) Найдите площадь сечения призмы плоскостью α, если призма правильная, cторона её основания равна 2√3, а боковое ребро равно 1. Задача 5. Основание четырёхугольной пирамиды SABCD – параллелограмм ABCD. а) Постройте сечение пирамиды плоскостью, проходящей через середину ребра AB параллельно плоскости SAD. б) Найдите площадь полученного сечения, если площадь грани SAD равна 16. Домашнее задание 1. Дан куб ABCDA1B1C1D1. Точка K – середина ребра C1D1. а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба. б) Найдите угол между плоскостями KBA1 и ADD1. 2. Дана правильная четырёхугольная пирамида MABCD, все рёбра которой равны 12. Точка N – середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2 : 1, считая от вершины M. а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией. б) Найдите площадь этого сечения |
