термех экзамен. Плоское движение твердого тела
 Скачать 126.5 Kb.
|
|
http://teormex.net Плоское движение твердого тела. П 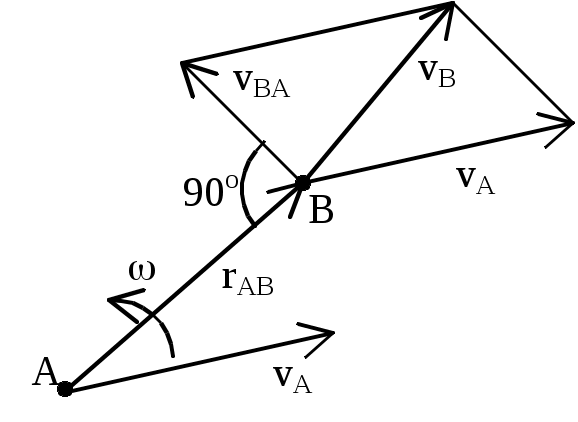 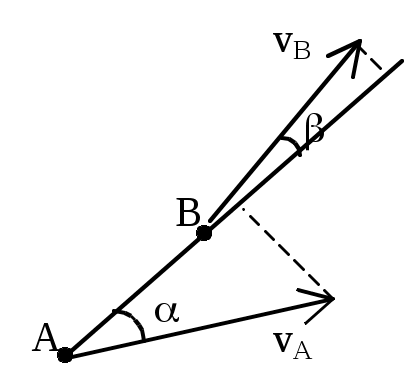 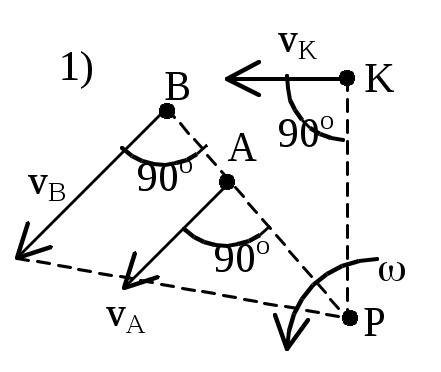 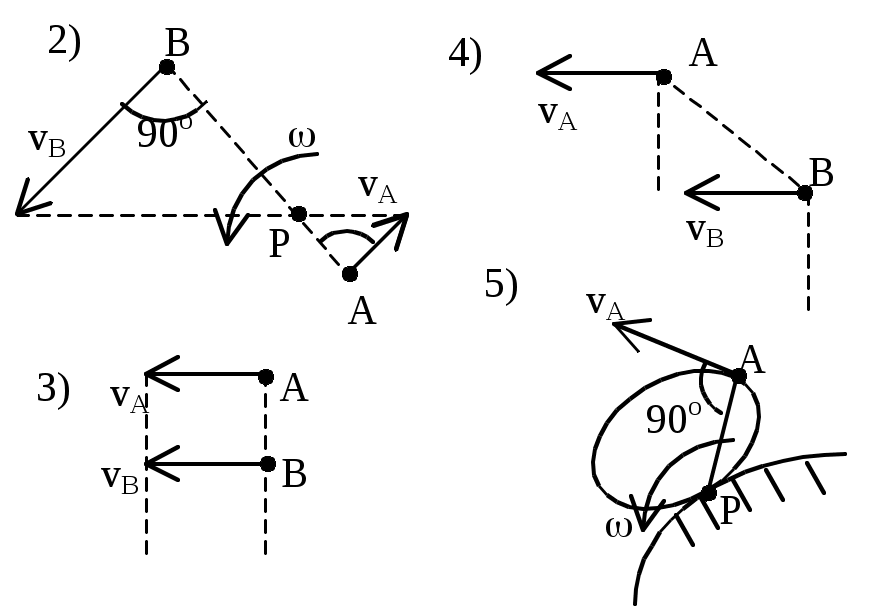 лоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости.Уравнения плоского движения: xA= f1(t), yA= f2(t), = f3(t), Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Скорости точек тела при плоском движении:  ;  , vBA= BAТеорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcos = vBcos. Мгновенный центр скоростей – точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если тело движется непоступательно, т.е. 0, то мгн.цент.ск. всегда существует. При поступательном движении м.ц.с. находится в .  – скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена этому отрезку в сторону вращения фигуры.  , скорости точек тела пропорциональны их расстояниям до м.ц.с.  , угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с. Определение положения м.ц.с.: 1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К); 2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. vA и vB); 3) если они при этом равны между собой, то м.ц.с. находится в , а угловая скорость =vA/=0; 4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в , и угловая скорость =vA/=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания. |