конспект урока: решение задач. 01.02.2022 Решение задач. Конспект! Тема Решение задач Геометрический смысл производной Задача 1

• Название: Конспект! Тема Решение задач Геометрический смысл производной Задача 1
• Анкор: конспект урока: решение задач
• Дата: 05.09.2022
• Размер: 23.23 Kb.
• Имя файла: 01.02.2022 Решение задач.docx
• Тип: Конспект; #662530

Сделать конспект!

Тема: Решение задач

Геометрический смысл производной

Задача 1. 

Найти тангенс угла наклона касательной к графику функции у=х³–х   в точке х0=1 .

Решение. 

Из геометрического смысла производной получаем, что производная функции у=ƒ(х), вычисленная при заданном значении х0, равна тангенсу угла, образованного положительным направлением оси   и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой х0, то есть

ƒ'(х0)=tgα

Найдем производную от заданной функции:

ƒ'(х)=(х³–х)'=3х²–1

в точке х0=1  имеем:

ƒ'(1)=2

Тогда окончательно получим, что

tgα =2

Ответ: tgα =2 
Механический смысл производной

Задача 2. 

Точка движется по закону х(t)=2t³–3t . Чему равна скорость в момент времени t=2 ?

Решение. 

Найдем скорость точки как первую производную от перемещения:

υ(t)=x'(t)=(2t³–3t )'=(2t³)'– (3t)'=2(t³)'–3(t)'=6t²–3

В момент времени t=2   скорость равна

υ(2)=6·2² – 3=21

Ответ: υ(2)=21

Уравнение касательной к графику функции

Задача 3. 

Записать уравнение касательной к графику функции у=х³+3х²–2х+9  в точке х0= –2 

Решение. 

Найдем значение функции в заданной точке:

у(–2)= (–2)³+3·(–2)² –2·(–2)+9=–8+12+4+9=17

Найдем производную заданной функции по правилу дифференцирования суммы(разности):

у'=(х³+3х²–2х+9)'=(х³)'+3·(х²)'–2·(х)'+9'=3х²+6х–2

у'=3х²+6х–2

Вычислим её значение в заданной точке

у'(–2)=3·(–2)²+6·(–2)–2=12–12–2= –2

Используя формулу:

у=у0+ƒ'(х0)(х–х0)

запишем уравнение касательной:

у=17+(–2)(х–(–2))=17–2(х+2)= –2х+13

Ответ: уравнение касательной: у= –2х+13
Примеры для самостоятельного решения.

1. Найти тангенс угла наклона касательной в точке х0= –1 к графику функции y = x⁴ + 3x² + 2x.

2. Прямолинейное движение точки задано уравнением s=3t² –6t+25

(t –выражено в секундах, s – в метрах). Найти скорость движения точки в момент времени t =4.

3. Напишите уравнение касательной к графику функции y = 2x² – 4x + 3 в точке х0=5
4. Вычислить производную функции у= 2х³+3х²–36х+90  в точке х=4 

5. Вычислить производную функции у=   в точке х= –3

6. Найти производные функций: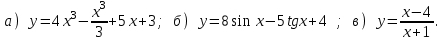

г) у= ;