Конспект урока Цели Ввести понятие параллелограмм
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
Разработка урока по наглядной геометрии для учащихся шестых классов по теме «Параллелограмм»Конспект урока Цели: Ввести понятие «параллелограмм». С помощью наглядных и практических упражнений конструктивного изобразительного характера ознакомить учащихся со свойствами противолежащих сторон и углов параллелограмма, диагоналей параллелограмма. Научить способам построениям параллелограмма, основанным на открытых учащимися свойствах параллелограмма. Сформировать у учащихся динамичный образ параллелограмма, которым несложно манипулировать мысленно. Ознакомить с классификацией параллелограммов и свойствами различных видов параллелограммов. Развивать геометрическое мышление, творческие способности. Развивать изобразительно-графические умения, измерительные навыки. Ход урокаОрганизационный момент.Проаверочная работа Устная работа. Формулировка темы урока.Параллелограмм. Запишите в тетради тему урока. Работа по новой темеУчитель работает у доски. Учитель: Проведем две пары параллельных прямых следующим образом. m||n, k||l  Рассмотрим образовавшийся при этом четырехугольник ABCD.  Его стороны попарно параллельны: AB||CD, BC||AD. Такой четырехугольник называют параллелограммом. Слово «параллелограмм» греческого происхождения, в переводе оно означает «изображающийся параллельными». – Ты не знаешь, сколько грамм Весит параллелограмм? Не могу понять, в чем дело? Сколько это, «параллело»? – Где, дружок, твоя культура? Параллелограмм – фигура, Знает каждый школьник в мире. У него сторон – четыре. Их рисуют не бесцельно, А попарно параллельно. Устно, используя рисунок на доске. Учитель: Назовите все параллелограммы, которые вы видите на рисунке.  Работа в тетрадях Учитель: Начертите в тетради, используя свойства клетчатой бумаги, какой-нибудь параллелограмм. Эксперимент. Перед вами лежит лист, на котором изображен параллелограмм ABCD, калька и булавка. Проведите диагонали параллелограмма и обозначьте точку пересечения буквой O. Наложите на параллелограмм кальку, скопируйте на нее параллелограмм и проткните в точке O булавкой. Поверните параллелограмм на 180 и определите новое положение каждой вершины; каждой стороны, диагоналей параллелограмма. Какие выводы можно из этого сделать? Что можно сказать про противоположные стороны параллелограмма? 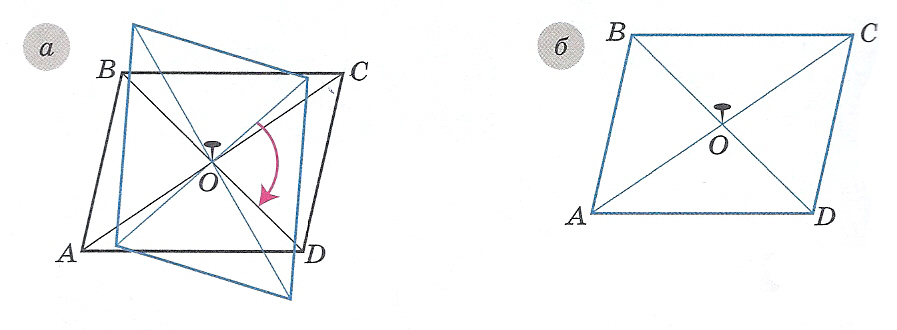 Ученик: Контуры параллелограмма на листе и на кальке при повороте на 180 совпали. Противоположные стороны параллелограмма равны. Учитель: Что можно сказать про противоположные углы параллелограмма? Ученик: Противоположные углы также равны. Учитель: В какой треугольник перейдет треугольник ABC? Треугольник ABO? Какой вывод можно сделать? Ученик: Диагональ делит параллелограмм на два равных треугольника. При повороте отрезок OA и отрезок OC, а также отрезок OB и отрезок OD поменялись местами. Это означает, что диагонали точкой пересечения делятся пополам. Учитель: Таким свойством обладают диагонали только параллелограммов. Параллелограмм является центрально симметричной фигурой. Центром симметрии параллелограмма является точка пересечения его диагоналей. Это свойство дает нам удобный способ его построения. Построение параллелограмма. Учитель выполняет построение у доски, учащиеся одновременно работают в тетрадях.  Упражнения Начертите в тетрадях два разных параллелограмма, диагонали которых равны 4 и 6 сантиметров. Постройте параллелограмм, диагонали которого равны 4 и 5 сантиметров и пересекаются под углом 30. В тетради отметьте три точки, не лежащие на одной прямой. Эти точки являются вершинами параллелограмма. Постройте все возможные параллелограммы, три вершины которых лежат в этих точках. Указание: используйте карандаши разных цветов Начертите в тетради произвольный четырехугольник (не параллелограмм). Отметьте середину сторон. Соедините их отрезками. Посмотрите на получившийся четырехугольник у себя и у своих соседей. Обратите внимание, что получился четырехугольник одного и того же вида. Как называется такой четырехугольник? Теперь вы знаете еще один способ построения произвольного параллелограмма. Четырехугольник ABCD – не параллелограмм, но у него есть одна пара параллельных сторон, одна пара равных сторон. Нарисуйте такой четырехугольник. Учитель: Четырехугольник, у которого две стороны параллельны, а две другие – не параллельны, называется трапецией. ФизкультминуткаА теперь, ребята, встали. Быстро руки вверх подняли Все умеем мы считать Раз, два, три, четыре, пять Раз! Подняться потянуться. (Под счет учителя дети выполняют потягивания.) Два! Согнуться, разогнуться. (Наклоны. Повороты туловища.) Три! В ладоши три хлопка, Головою три кивка. (Движения головой.) На четыре - руки шире. (Хлопки в ладоши.) Пять — руками помахать. (Движения руками.) Шесть — за парту тихо сесть. (Прыжки. Ходьба на месте.) Нарисуй глазами треугольник. Теперь его переверни вершиной вниз. И вновь глазами ты по периметру веди. Рисуй восьмерку вертикально. Ты головою не крути, А лишь глазами осторожно ты вдоль по линиям води. И на бочок ее клади. Теперь следи горизонтально, И в центре ты остановись. Зажмурься крепко, не ленись. Глаза открываем мы наконец. Зарядка окончилась. Ты молодец! Работа по новой теме (продолжение)Вниманию учащихся предлагается плакат с изображениями видов параллелограммов. 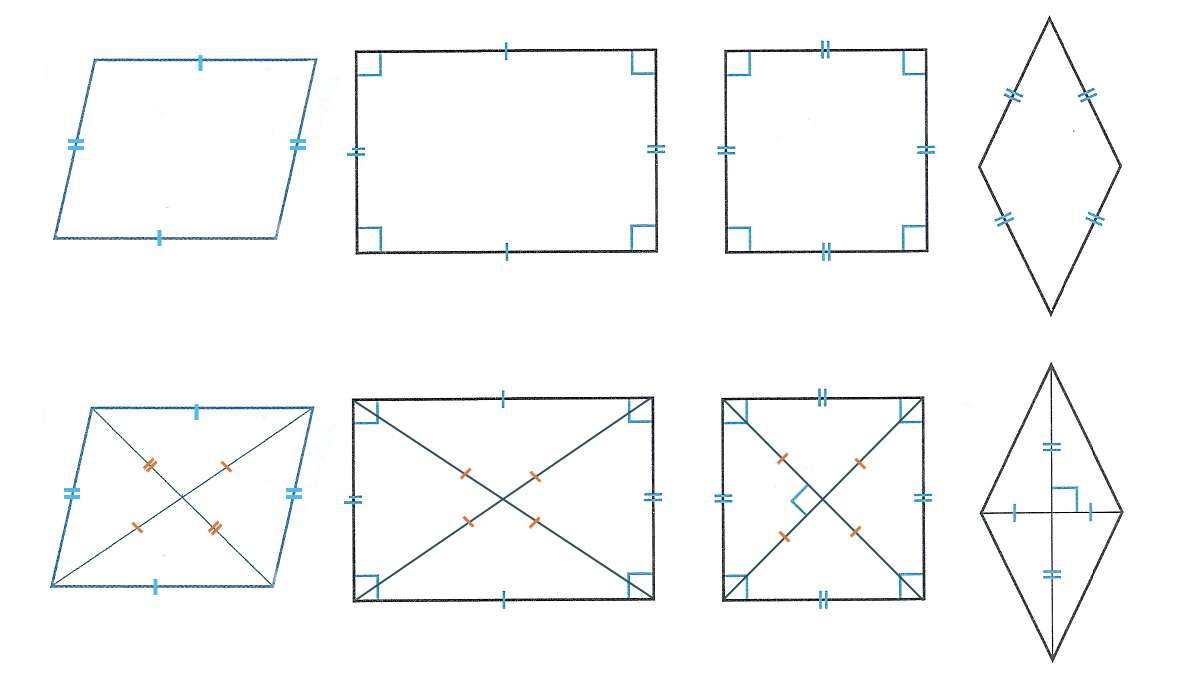 Учитель: Да, да, не удивляйтесь. И ромб, и прямоугольник, и квадрат – тоже параллелограммы. Только параллелограммы с некоторыми дополнительными свойствами. Прямоугольник – это параллелограмм, у которого все углы прямые. Ромб – это параллелограмм, у которого все стороны равны. Диагонали ромба, кроме свойств, присущих всем параллелограммам, обладают еще одним: они перпендикулярны друг другу. Квадрат – очень интересный четырехугольник. Ему можно дать несколько определений. У квадрата, как и у ромба, все стороны равны. Только еще все углы прямые. Значит, квадрат – это ромб с прямыми углами. У квадрата, как и у прямоугольника, все углы прямые. Только еще все стороны равны. Значит, квадрат – это прямоугольник, у которого все стороны равны. У квадрата, как и у параллелограмма, стороны попарно параллельны. Только еще все они равны, и все углы прямые. Значит, квадрат – это параллелограмм с прямыми углами, у которого все стороны равны. Опыты с листом бумаги. Из куска бумаги произвольной формы сложите, а затем вырежьте прямоугольник. Покажите в нём параллельные и перпендикулярные стороны. Сверните прямоугольник так, чтобы получился квадрат. Вырежьте квадрат и исследуйте его. Получите перегибанием две диагонали. Какие свойства вы можете отметить, используя только перегибы и наложения бумаги? Используйте следующий план исследования: 1.Сравните диагонали по длине. 2.Как диагонали расположены относительно друг друга? 3.Как диагонали делятся точкой пересечения? 4.На какие фигуры делит квадрат каждая диагональ? 5.Какого вида эти фигуры? 6.Сравните их между собой. Подведение итогов урока.С какими замечательными четырехугольниками вы познакомились сегодня на уроке? Какими свойствами обладает параллелограмм? Назовите виды параллелограммов. Теперь послушайте сказку-вопрос и дайте свои ответы. Собрались все четырехугольники на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и никак не могли придти к единому мнению. И вот один старый параллелограмм сказал: «Давайте все отправимся в царство четырехугольников. Кто первым придет, тот и будет королем» Все согласились. Рано утром отправились все в далекое путешествие. На пути путешественников повстречалась река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам» Часть четырехугольников осталась на берегу, остальные благополучно переплыли и отправились дальше. На пути им повстречалась высокая гора, которая сказала, что даст пройти только тем, у кого диагонали равны. Несколько путешественников осталась у горы, остальные продолжили путь. Дошли до большого обрыва, где был узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошел только один четырехугольник, который первым добрался до царства и был провозглашен королем. Вопросы: 1. Кто стал королем? 2. Кто был его основным соперником? 3. Кто первым вышел из соревнования? Домашнее задание
ЛитератураМатематика. Арифметика. Геометрия. 6 класс: учеб. для общеобразоват. учреждений / Е.А. Бунимович, Л.Е. Кузнецова, С.С. Минаева и др.; Рос. акад. наук, Рос. акад. образование. - М.: Просвещение, 2010 Математика: учеб. для 6 кл. / Под ред. Г.В. Дорофеева, И.Ф.Шарыгина.- М.:Просвещение, 2008 План-конспект урока по геометрии (8 класс) по теме: Урок-зачет.Четырехугольники. Миронова Людмила Михайловна ( http://nsportal.ru/shkola/geometriya/library/urok-zachetchetyrehugolniki ) Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия.- М.: Дрофа, 2008 В разработке урока использовались материалы курса "Методика преподавания наглядной геометрии учащимся 5-6 классов" / Л.О.Рослова.- М.: Педагогический университет "Первое сентября", 2009 |