решение систем уравнений. конспект 8 кл алг. Конспект урока по алгебре, 8 класс Тема урока решение систем уравнений известными способами Тип урока урок систематизации и обобщения Цели урока
 Скачать 20 Kb. Скачать 20 Kb.
|
|
Конспект урока по алгебре, 8 класс Тема урока: решение систем уравнений известными способами Тип урока: урок систематизации и обобщения Цели урока: 1) Образовательная: закрепление навыков решения систем уравнений различными методами; выработка умений пользоваться всеми методами решения систем уравнений; решение типовых и повышенного уровня сложности задач по теме; 2) Развивающая: развивать умение обрабатывать информацию, формировать коммуникативную компетенцию 3) Воспитательная: воспитание аккуратности, математической культуры учащихся, внимательности, дисциплинированности, усидчивости Результаты урока: 1) Предметные: тренировать навык нахождения количества решений систем уравнений; тренировать навык решения системы уравнений выбранным методом; 2) Личностные: формировать познавательную активность и мотивацию учебной деятельности учащихся; воспитывать аккуратность, самостоятельность и коллективность; развивать рефлексивные умения через проведение анализа результатов урока. 3) Метапредметные: развивать умение анализировать информацию при работе с презентацией; развивать умение работать самостоятельно. Тема предыдущего урока: решение систем способом подстановки. Тема следующего урока: проверочная работа (20 мин) + решение задач с помощью систем уравнений Структура (планурока): 1. Актуализация знаний: 1.1. орг. момент, устная проверка домашнего задания (называют способ решения и ответ) 1.2. фронтальный опрос с целью актуализации знаний; 2. Применение новых знаний: 2.1. групповая работа – тренировка навыка решения систем уравнений всеми изученными методами 2.2. Решение систем повышенной сложности у доски 2.3. подведение итогов урока, рефлексия, запись дз. Ход урока: -Здравствуйте, ребята! Староста назовите отсутствующих. Есть ли вопросы по выполнению домашнего задания? Если нет, то переходим к проверки ответов и способов решения(устно). Если есть вопросы, то решаем задания у доски (решает ученик, который справился с заданием, объясняет все). Если у всех сложности, то объясняет учитель. Фронтальный опрос: 1) Какая пара чисел является решением системы уравнений? (решают в тет) 2) Укажите систему уравнений, которая имеет два решения.(устно) 4) Воспользовавшись графическим методом, ответьте на вопрос: сколько решений имеет система уравнений? (у доски) 5) Назовите основные шаги решения системы уравнений способом подстановки групповая работа – тренировка навыка решения систем уравнений всеми изученными методами Порядок организации групповой работы: · класс разбивается на группы по 4 человека; · учитель ставит перед учащимися цель групповой работы: решить с помощью различных методов системы уравнений, текст которых дан на карточках; определяется порядок работы в группе; · считается, что группа решила задания только тогда, когда каждый член группы записал решение в тетрадь и произошло групповое обсуждение решений всех заданий; · учитель вызывает любого ученика из этой группы для записи итоговых ответов решений в сводную таблицу · после окончания заполнения сводной таблицы выполняется проверка ответов и подводится окончательный итог групповой работы. Карточка 1 группы: 1 задание. 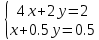 2 задание: 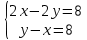 3 задание: 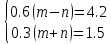 4 задание: 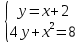 5 задание: убедитесь в том, что графической моделью системы являются совпадающие прямые 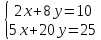 Карточка 2 группы: 1 задание: 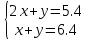 2 задание: 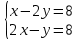 3 задание: 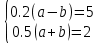 4 задание: 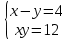 5 задание: убедитесь в том, что графической моделью системы являются совпадающие прямые 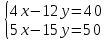 Карточка 3 группы: 1 задание: 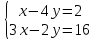 2 задание: 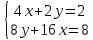 3 задание: 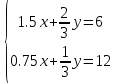 4 задание: 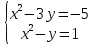 5 задание: убедитесь в том, что графической моделью системы являются параллельные прямые 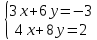 Решение систем повышенной сложности у доски: Из учебника: №659(бв), №661 (в) Дз: 658, 656 |
