|
|
линейная функция ПЛАН. Конспект урока по теме Линейная функция. Тема урока Линейная функция Цели урока Предметные ууд формирование понятие линейная функция
Конспект урока по теме «Линейная функция»
.
Тема урока: «Линейная функция»
Цели урока:
Предметные УУД:
-формирование понятие линейная функция
Метапредметные УУД:
Регулятивные:
- развитие умений сравнивать, обобщать, выделять главное, умений логически мыслить.
Познавательные :
- осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы;
Коммуникативные:
- формирование умения работать по заданному алгоритму, аргументировать ответ или ошибку;
- контролировать действие партнера.
Личностные УУД:
положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения.
Тип урока: урок формирования понятия линейная функция
Формы организации познавательной деятельности обучающихся: коллективная, индивидуальная, работа в парах.
Ход урока:
Подготовительный этап.
Цель: актуализировать знания: прямоугольной системы координат; функциональной зависимости; способов задания функции; понятие прямой и обратной пропорциональных зависимостей.
Актуализация умений: построение графика функции.
Орг.момент.
Учитель: давайте выполним задания, представленные на слайде
Задание №1. Назовите абсциссу и ординату следующих точек:
А(-6;2); В(5;-7); С(-7;0)
Задание № 2.Назовите зависимую и независимую переменные, какая из них является аргументом, а какая функцией:
Y(x)=215x; 2) F(x)=2-5x2; 3) S(t)=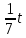
Задание № 3. Выдается в виде раздаточного материала.
Дана функция y=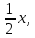 заполнить таблицу: заполнить таблицу:
Задание № 4. Дана функция, выяснить, принадлежит ли точка А (-1;5) графику данной функции y=x|2.
Задание № 5 Назовите коэффициенты функции:
Y=2x; y=x; y=7x+4; y=-x.
Задание № 6. Определить по графику вид функции:
Мотивационный этап.
Цель: возбуждение интереса к изучению понятия линейная функция.
Учитель: При выполнении задания № 6 под буквой В у Вас возникли трудности. С чем они связаны?
Дети: Мы не знаем, какой вид функции задает данный график.
Учитель: Исходя из того, что мы столкнулись с ситуацией, в которой наших знаний не достаточно, давайте вместе определимся, чем мы будем сегодня заниматься на уроке.
Дети: Мы будем изучать новый вид функции и ее графика.
Введение понятия линейная функция в содержание обучения.
Цель: Ввести определение понятия линейная функция
Способ введения: абстрактно-дедуктивный.
А) вводим термин:
Учитель: Сегодня мы познакомимся с функцией другого вида, её графиком.
Задача №591(а). На складе 400 тонн угля. Ежедневно стали подвозить по 50 тонн. Сколько угля(у) будет на складе через2,4,10, х дней? Выполнить задание.№591(б) На складе было 400 тонн угля. Ежедневно стали увозить по 50 тонн угля. Сколько угля (у) будет на складе через х дней? Проверьте. Вычислите значение у при х=2, х=5? Выполнить задание №592. Турист проехал от города 10км на автобусе, а затем продолжил движение в том же направлении пешком со скоростью 5км/ч. На каком расстоянии (у) от города турист был через х часов ходьбы? Вычислите значение у при х=2, при х=3?
(У=50х+400, через 2 дня – 500 т, через 4 дня – 600 т, через 10 дней - 900 т
У=400-50х, через 2 дня- 300 т, через 5 дней – 150 т
У=5х+10, через 2 ч- 30 км
Через 3 ч – 35 км)
Эти задачи можно решить с помощью функции.
Сделайте обобщение решенных заданий. Что общего в полученных выражениях
Дети: все выражения состоят из двух слагаемых, одно с переменной , а другое без; значение этого выражения зависит от значения перемнной x.
Учитель: Зависимость такого вида мы будем называть линейной функцией, то есть :
- мы увидели зависимость;
- эта зависимость задана определенным правилосм;
- значения этой зависимости существуют только на определенном множестве.
Учитель: Линейная функция - это функция вида у=кх+в где к, в-числа. Х-независимая переменная(аргумент), У-зависимая переменная(функция)
Можно показать, что графиком линейной функции y = kx + b, так же, как и функции у = кх, является прямая (установите это опытным путем самостоятельно). Так как прямая определяется двумя ее точками, то для построения графика функции y = kx + b достаточно построить две точки этого графика.
Дети: Функция у = кх также является линейной (это частный случай функции у = кх + b при b = 0).
Давайте построим график зависимости
.
Определение линейной функции смотрим в учебнике.
Определение: функция вида y=kx+b называется линейной, где k и b – заданные числа. Графиком линейной функции является прямая, не проходящая через начало координат.
Выделяем существенные признаки:
- функция, то есть зависимость;
- задана определенным законом kx+b
- расположена на некотором множестве
Построить график функции у = 2х + 5. При х = 0 значение функции у = 2х + 5 равно 5, т. е. точка (0; 5) принадлежит графику. Если х = 1, то у = 2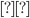 1 + 5 = 7, т. е. точка (1; 7) также принадлежит графику. Построим точки (0; 5) и (1; 7) и проведем через них прямую. Эта прямая и является графиком функции y = 2х + 5 (рис. 1а). Заметим, что каждая точка графика функции у = 2х + 5 имеет ординату, на 5 единиц большую, чем точка графика функции у = 2х с той же абсциссой. Это означает, что каждая точка графика функции у = 2х + 5 получается сдвигом на 5 единиц вверх вдоль оси ординат соответствующей точки графика функции у = 2х. График функции y = kx + b получается сдвигом графика функции y = kx на b единиц вдоль оси ординат. Графиками функций y = kx и y = kx + b являются параллельными прямыми. Отметим, что для построения графика линейной функции иногда удобно находить точки пересечения этого графика с осями координат. б) Найти точки пересечения графика функции у= - 2х + 4 с осями координат и построить график. Найдем точку пересечения графика с осью абсцисс. Ордината этой точки равна 0. Поэтому - 2х + 4 = 0, откуда х = 2. Итак, точка пересечения графика с осью абсцисс имеет координаты (2; 0). Найдем точку пересечения графика с осью ординат. Так как абсцисса этой точки равна 0, то у = -2 1 + 5 = 7, т. е. точка (1; 7) также принадлежит графику. Построим точки (0; 5) и (1; 7) и проведем через них прямую. Эта прямая и является графиком функции y = 2х + 5 (рис. 1а). Заметим, что каждая точка графика функции у = 2х + 5 имеет ординату, на 5 единиц большую, чем точка графика функции у = 2х с той же абсциссой. Это означает, что каждая точка графика функции у = 2х + 5 получается сдвигом на 5 единиц вверх вдоль оси ординат соответствующей точки графика функции у = 2х. График функции y = kx + b получается сдвигом графика функции y = kx на b единиц вдоль оси ординат. Графиками функций y = kx и y = kx + b являются параллельными прямыми. Отметим, что для построения графика линейной функции иногда удобно находить точки пересечения этого графика с осями координат. б) Найти точки пересечения графика функции у= - 2х + 4 с осями координат и построить график. Найдем точку пересечения графика с осью абсцисс. Ордината этой точки равна 0. Поэтому - 2х + 4 = 0, откуда х = 2. Итак, точка пересечения графика с осью абсцисс имеет координаты (2; 0). Найдем точку пересечения графика с осью ординат. Так как абсцисса этой точки равна 0, то у = -2 0 + 4 = 4. Итак, точка пересечения графика с осью ординат имеет координаты (0; 4). График функции у= - 2x + 4 изображен на рисунке 1б. Слайд 9-11 0 + 4 = 4. Итак, точка пересечения графика с осью ординат имеет координаты (0; 4). График функции у= - 2x + 4 изображен на рисунке 1б. Слайд 9-11
Построить график линейной функции y = kx + b при k = 0, b = 2. Если k = 0 и b = 2, то у = 2. Ординаты всех точек графика равны 2, и поэтому графиком функции является прямая, параллельная оси Ох и проходящая через точку (0; 2)
С этой целью, попробуем выполнить следующее задание, расположенное на слайде:
Б) выделяем существенные признаки:
Учитель: ребята, как вы думаете, что объединяет данные графики?
Дети: все график функции представлены в виде прямых, которые не проходят через начало координат.
Учитель: На какие две группы можно разбить данные графики.
Дети: те которые лежат в первой и в третьей четвертях, и два графика расположены во второй и четвертой четвертях
Учитель: А как вы думаете, от чего зависит расположение графиков функции на координатной плоскости?
Дети: от формулы, которая его задает.
Учитель: Давайте вспомним, графиком какой функции является прямая?
Дети: прямая пропорциональность или функция вида y=kx.
Учитель: А чем отличается график функции прямой пропорциональности от рассмотренных нами на данном уроке?
Дети: наша прямая не проходит через начало координат.
Учитель: Посмотрите еще на наши графики и попробуйте проанализировать в каких точках прямая пересекает ось ОУ.
Дети: на двух поднялся, на двух опустился на столько то ед.отрезков.
| |
|
|
 Скачать 23.08 Kb.
Скачать 23.08 Kb.
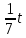
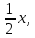 заполнить таблицу:
заполнить таблицу: