программа. Программирование_Паскаль_ЛабРаб 1 семестр. Контроль обучения 4 Первое контрольное задание 5 Второе контрольное задание 31

• Название: Контроль обучения 4 Первое контрольное задание 5 Второе контрольное задание 31
• Анкор: программа
• Дата: 09.04.2023
• Размер: 0.69 Mb.
• Имя файла: Программирование_Паскаль_ЛабРаб 1 семестр.doc
• Тип: Документы; #1048084
• страница: 1 из 3

СОДЕРЖАНИЕ

Контроль обучения 4

Первое контрольное задание 5

Второе контрольное задание 31

Третье контрольное задание 65

Контроль обучения

Дисциплина «Программирование и основы алгоритмизации» изучается на протяжении одного семестра. В процессе дистанционного обучения дисциплине студент должен выполнить три контрольных заданий и компьютерную экзаменационную работу. Каждое контрольное задание требует создания нескольких программ.

Студент должен выполнить свой вариант заданий.
Составленные и отлаженные программы (обязательно с комментариями в тексте) студент по мере освоения программирования периодически пересылает в папку Гость/Отчеты/имя личной папки. При правильном выполнении программы студент получает подтверждение о том, что они зачтены. Если программа составлена неправильно, студент получает описание ошибок программы. В конце семестра студент выполняет экзаменационную работу.

Первое контрольное задание

Первое контрольное (текстовое) задание посвящено созданию программ с использованием простых управляющих структур: условного оператора, цикла. В этом задании используются простые типы данных и нет необходимости использовать массивы. Поэтому не засчитываются программы, написанные с использованием массивов. Кроме того, требуется писать программы в рамках структурного программирования. В частности, запрещается использовать операторы перехода и метки.

Задание состоит из трех задач, вам требуется составить программы на языке Паскаль. В некоторых программах полезно определить какие-то вспомогательные функции.

Многие задачи из этой контрольной имеют вид: «Дана последовательность из n (действительных) целых чисел. Определить (вычислить) …» или «Даны натуральное n и вещественные числа a₁, a₂, ..., a_n. Определить (вычислить) …» и подобного рода. Во всех этих задачах не требуется хранения исходных последовательностей значений. Вы вводите n, потом в цикле, работающем n раз, осуществляете пошаговый ввод чисел и каким-то образом постепенно вычисляете необходимый результат.
Примеры задач с решением

1. 
   Вычислить: y = sin1 + sin1.1 + sin1.2 + ... + sin2.
   

Первый вариант решения данной задачи.

Анализируя данную формулу, видим, что аргумент функции sin очередного слагаемого отличается от предыдущего на 0.1. Поэтому для решения данной задачи можно составить следующий алгоритм.
Переменные:

с – очередное слагаемое;

i – аргумент функции;

y – сумма.

1. 
   Обнуляем начальное значение переменной y  строка 5, в которой будем накапливать сумму.
   
2. 
   Начальное значение аргумента функции i равно 1 (строка 6).
   
3. 
   Проверяем, значение i меньше или равно 2, т.к. по заданию аргумент функции изменяется от 1 до 2 (строка 7).
   
4. 
   Если «да», то определяем очередное значение функции (строка 9). Сохраняем его в переменной с. Если «нет», то расчет суммы закончен – переходим на шаг 8.
   
5. 
   Добавляем это слагаемое в сумму (строка 10).
   
6. 
   Увеличиваем значение аргумента i на 0.1 (строка 11).
   
7. 
   Переходим на шаг 3.
   
8. 
   Выводим результат на экран (строка 13).
   

1)	var y, c, i : real;
2)	begin
3)	writeln('Полученное значение расчета формулы ',
4)	'y=sin1+sin1.1+sin1.2+ ... +sin2 = ');
5)	y:=0;
6)	i:=1;
7)	while i <=2 do
8)	Begin
9)	c := sin(i);
10)	y:=y+c;
11)	i:=i+0.1;
12)	end;
13)	writeln(y);
14)	end.

Второй вариант решения данной задачи.

Анализируя данную формулу, видим, что каждое слагаемое данной суммы можно рассчитать по формуле sin(1 + 0.1 * i), где i изменяется от 0 до 10. Поэтому для решения данной задачи можно составить следующий алгоритм.
Переменные:

i – параметр цикла;

y – сумма.

1. 
   Обнуляем начальное значение переменной y  строка 6, в которой будем накапливать сумму.
   
2. 
   Организуем цикл для определения суммы (параметр данного цикла должен измениться от 0 до 10) .
   
3. 
   В данном цикле определяем очередное слагаемое по формуле и добавляем это слагаемое в сумму (строка 7).
   
4. 
   Выводим результат на экран (строка 8).
   

1)	var y : real;
2)	i : integer;
3)	Begin
4)	writeln('Полученное значение расчета формулы ',
5)	'y=sin1+sin1.1+sin1.2+ ... +sin2 = ');
6)	y:=0;
7)	for i:=0 to 10 do y:=y+sin(1+0.1*i);
8)	writeln(y);
9)	end.

2. Вычислить: y = 1*3*5* ... *(2n–1), n>0;
var y : real;

i, n : integer;

begin

writeln('Введите количество чисел');

readln(n);

y:=1;

for i:=1 to n do y:=y*(2*i–1);

writeln('Полученное значение y= ', y)

end.
3. Дано натуральное число N. Разложить его на простые множители.
Переменные:

n  исследуемое число;

i, j  переменные циклов;

f  вспомогательный флаг.
Алгоритм решения задачи:

1. Вводим значение переменной n. Т.к. пользователь может случайно ввести отрицательное число, то необходимо дать ему возможность для повторного ввода значения переменной n. Поэтому организуем цикл (строки 3–6 текста программы). Лучше использовать цикл с постпроверкой условия (Repeat…Until). Тело цикла составляют два оператора: оператор вывода на экран приглашения для ввода значения переменной n (строка 4) и оператор чтения с клавиатуры – для непосредственного ввода значения переменной n (строка 5). Данный цикл будет выполняться до тех пор, пока пользователь не введет любое положительное число (срока 6).

2. Выводим на экран значение переменной n и начинаем формировать ответ. Ответ будет представлен в следующем виде (например, в качестве значения переменной n ввели 8):
8 = 1*2*2*2. Т.к. единица является простым множителем для любого числа, то выводим ее на экран (строка 7). В результате выполнения данной строки на экране появится: 8=1.

3. Вспомогательной переменной f присваиваем значение false. Данная переменная нам будет необходима для определения, были ли вообще найдены простые множители у заданного числа n. Запоминаем исходное значение переменной n в переменной j (строка 8).

4. В цикле по переменной i начинаем порождение натуральных чисел, не превосходящих середину заданного числа n, для определения делителей данного числа n (строка 9). Данный цикл начали с 2, т.к. единицу мы уже учли (шаг 2 данного алгоритма). Т.к. в цикле For можно использовать только целые переменные, поэтому воспользовались оператором целочисленного деления на 2 (n div 2). В данном цикле выполняем следующее.

Определяем, является ли очередное i делителем числа n (в качестве n в данном цикле используем j). Для этого определяем остаток от деления j на i. Если остаток равен 0 (строка 10), т.е. число i является делителем j, то определяем, сколько таких делителей, уменьшая число n (строки 11–18). Переменной f присваиваем значение true (строка 12) – это означает, что у заданного числа n есть делители. Организуем цикл, пока остаток от деления j на i равен 0 (строка 13). В данном цикле выводим делитель на экран (строка 15) и уменьшаем заданное число, деля его целочисленно на делитель (строка 16). Повторяем цикл.

После завершения этого цикла возвращаемся на цикл For (строка 9), изменяем i и повторяем те же действия для нового делителя.

5. Если у числа нет делителей (оно является простым), то данное число можно разложить только на 1 и само на себя. Вспомогательная переменная f и определяет, были ли делители у числа n. Если значение переменной f осталось false, то делителей не было, поэтому выводим само это число (строка 19).

1)	var i, n, j : integer; f: boolean;
2)	begin
3)	repeat
4)	write('Введите натуральное число N= ');
5)	readln(n);
6)	until n>0;
7)	write (N:6, '=1');
8)	f:=false; j:=n;
9)	for i:=2 to n div 2 do
10)	if j mod i = 0 then
11)	begin
12)	f:=true;
	{цикл определят, сколько таких множителей i в нашем числе n}
13)	while j mod i=0 do
14)	begin
15)	write('*', i);
16)	j:=j div i;
17)	end;
18)	end;
	{f определяет, были ли найдены простые множители,
	большие единицы}
19)	if not f then writeln('*', n);
20)	writeln
21)	end.

4. Даны натуральное n и последовательность a₁, a₂,…,a_n вещественных чисел. Найдите знакочередующую сумму S = a₁a₂+ a₃… + (1)ⁿ⁺¹ a_n.
Переменные:

n – количество чисел;

a – очередное число;

p – булевский признак знака слагаемого;

i – переменная цикла;

S – знакочередующая сумма чисел.
Алгоритм решения задачи:

1. 
   вводим длину последовательности n и устанавливаем начальное значение S;
   
2. 
   булевская переменная p первоначально истинна, она будет указывать на знак слагаемого в сумме;
   
3. 
   последовательно считываем числа и, если p = true, то прибавляем его к сумме S, иначе отнимаем;
   
4. 
   на каждом шаге цикла значение p меняем на противоположное;
   
5. 
   выводим результат.
   

var n, i : integer;

a, S : real;

p: boolean;

begin

repeat

write('Введите длину последовательности n=');

readln(n);

until n>0;

p:= true;

S:=0;

for i:=1 to n do

begin

write('Введите a=');

readln(a);

if p then S:=S+a else S:=S–a;

p:= not p

end;

writeln('Знакочередующая сумма чисел S= ', S);

end.
5. Найти сумму первых n членов ряда y = 1 + x/2 + x²/3 + +x³/4+..., при |x|<1.
Переменные:

n – количество членов ряда;

x – переменная ряда;

z – вспомогательная переменная;

i – переменная цикла;

y – сумма ряда.
Алгоритм решения задачи:

1) вводим количество членов ряда n и переменную x;

2) в цикле порождаем очередной член ряда и прибавляем его к сумме y;

3) выводим результат.
var x, y, z : real;

n, i : integer;

begin

repeat

writeln('Введите переменную ряда x, |x|<1, x=');

readln(x);

write('Введите число членов ряда n=');

readln(n);

until (abs(x)<1) and (n>0);

y:=1; z:=1;

for i:=2 to n do

begin

z:=z*x;

y:=y+z/i;

end;

writeln('Сумма первых n членов ряда y =', y);

end.
6. Вводится последовательность из N целых чисел. Найти сумму всех отрицательных чисел.
Переменные:

n – количество чисел;

x – очередное число;

i – переменная цикла;

sum – сумма отрицательных чисел.
Алгоритм решения задачи:

1. 
   вводим длину последовательности n и устанавливаем начальное значение sum;
   
2. 
   последовательно считываем числа и, если число отрицательное, то прибавляем его к сумме sum;
   
3. 
   в зависимости от значения sum выводим результат.
   

var n, x, sum, i : integer;

begin

repeat

write('Введите длину последовательности n=');

readln(n);

until n>0;

sum:=0;

for i:=1 to n do

begin

write('Введите x='); readln(x);

if x<0 then sum:=sum+x;

end;

if sum=0 then writeln('Отрицательных чисел нет')

else writeln('Сумма отрицательных чисел sum= ', sum);

end.
7. Вводится последовательность из N целых чисел. Найти наибольшее число.
Переменные:

n – количество чисел;

x – очередное число;

i – переменная цикла;

max – наибольшее число.
Алгоритм решения задачи:

1. 
   вводим длину последовательности n и устанавливаем начальное значение max по первому числу;
   
2. 
   последовательно считываем числа и, если очередное число x больше max, то изменяем значение max := x;
   
3. 
   выводим результат.
   

var n, x, max, i : integer;

begin

repeat

write('Введите длину последовательности n=');

readln(n);

until n>0;

write('Введите x=');

readln(x);

max:=x;

for i:=2 to n do

begin

write('Введите x=');

readln(x);

if (x>max) then max:=x;

end;

writeln('Наибольшее из чисел max=', max);

end.
8. Вводится последовательность целых чисел, 0 – конец последовательности. Найти два наименьших числа.
Переменные:

x – очередное число;

min1 – первое наименьшее число;

min2 – второе наименьшее число (min2>=min1).
Алгоритм решения задачи:

1. 
   устанавливаем начальные значения min1 и min2 по двум первым числам;
   
2. 
   последовательно считываем числа и, если очередное число x меньше или равно min1 (min1
3. 
   если x попадает в интервал от min1 до min2, то изменяем только min2;
   
4. 
   выводим результат.
   

var x,min1,min2:integer;

begin

write('Введите x=');

readln(x);

min1:=x;

write('Введите x=');

readln(x);

min2:=x ;

{min1<=min2}

repeat

if x<=min1 then

begin

min2:=min1;

min1:=x;

end

else if (min1
write('Введите x=');

readln(x);

until (x=0);

writeln( 'Два наименьших числа равны', min1, 'и', min2);

end.
9. Вводится последовательность ненулевых чисел, 0 – конец последовательности. Определить, является ли последовательность возрастающей.
Переменные:

old – предыдущее число;

new – рассматриваемое число;

f – флаг.
Решение данной задачи строится от противного. Математически для того, чтобы последовательность была возрастающей, для каждого очередного элемента new и предыдущего old должно выполнятся условие new > old. Любое нарушение данного условия приводит к тому, что последовательность не может быть возрастающей.
Алгоритм решения задачи:

1. 
   вводим два первых числа как old и new, задаем начальное значение флага f;
   
2. 
   в цикле ищем нарушение свойства членов возрастающей последовательности;
   
3. 
   переприсваиваем значение old:=new и вводим новое – new;
   
4. 
   в зависимости от флага выводим результат.
   

var old, new : real;

f : boolean;

begin

write('Введите x=');

readln(old);

write('Введите x=');

readln(new);

f:=true;

repeat

if new<=old then f:=false;

old:=new;

write('Введите x=');

readln(new);

until new=0;

if f then writeln( 'Последовательность возрастающая')

else writeln( 'Последовательность не является возрастающей');

end.
10. Даны натуральное n и последовательность вещественных чисел a₁, a₂,…, a_n. Сколько отрицательных чисел в начале последовательности (до первого неотрицательного)?
Переменные:

k – счетчик;

i – переменная цикла;

n – количество членов последовательности;

a – очередной член последовательности;

p – признак отрицательного числа в начале последовательности.
Алгоритм решения задачи:

1. 
   вводим длину последовательности, задаем начальное значение счетчика k;
   
2. 
   устанавливаем признак отрицательного числа p=true;
   
3. 
   в цикле вводим очередной член последовательности;
   
4. 
   если это отрицательное число и до этого неотрицательных чисел не было, то увеличиваем значение счетчика на единицу;
   
5. 
   в противном случае, если член последовательности неотрицателен, то полагаем p=false;
   
6. 
   в зависимости от k выводим результат.
   

var a: real; p: boolean;

k,n : integer;

begin

repeat

write('Введите длину последовательности n=');

readln(n);

until n>0;

k:=0; p:=true;

for i:=1 to n do

begin

writeln('Введите число');

readln(a);

if (a<0) and p then k:=k+1else

if a>=0 then p :=false

end;

if k=0 then writeln('отрицательных чисел в начале нет')

else writeln('последовательность начинается с ', k, ' чисел')

end.
11. Дан прямоугольный бильярдный стол со сторонами А и В, где А, В – натуральные числа (бильярд Льюиса Кэрролла). Из угловой лузы вылетает шар под углом 45 градусов к боковым стенкам, ударяется о борт, отскакивает, ударяется еще раз и т.д., пока не вылетит через одну из угловых луз. Рассчитать количество отрезков в ломаной траектории шара. Считать угол падения равным углу отражения.
Данная задача решается с помощью стандартных функций выделения целой части от деления y на x (y div x) и выделения остатка y mod x. При прохождении шаром прямоугольного стола и отражении его от боковых сторон происходит увеличение числа отрезков траектории на два, а обратный путь вычисляется как y:=a–x+y mod x, где y – обратный путь для шара, a – длинная сторона стола, x – короткая сторона стола.
Переменные:

а) в функции bill:

x, y – два натуральных числа (формальные параметры);

k – вспомогательная переменная (локальная переменная);

a – длинная сторона стола (глобальная переменная);

б) в основной программе:

a, b – два натуральных числа (глобальные переменные).
Алгоритм решения задачи:

1. 
   создаем описание функции bill;
   
2. 
   вводим два натуральных числа a и b (не кратные друг другу);
   
3. 
   вызываем функцию bill для определения количества отрезков;
   
4. 
   завершаем работу программы.
   

var a, b : integer;

function bill(y,x:integer):integer;

var k:integer;

begin

k:=0;

while y mod x <>0 do

begin

k:=k+y div x+2;

y:=a–x+y mod x;

end;

bill:=k;

end;

begin

repeat

writeln('Введите два натуральных числа A>B');

readln(a,b);

until a>=b;

writeln('Количество отрезков в траектории :', bill(a,b));

end.
12. Пусть процедура maxmin(x,y) присваивает параметру x большее из вещественных чисел x и y, а параметру y – меньшее. Описать данную процедуру и использовать ее для перераспределения значений вещественных переменных a, b и c так, чтобы стало a>=b>=c.
var a,b,c : real;

procedure maxmin( var x,y:real);

var r:real;

begin if xbegin

writeln('Введите три числа a,b,c –');

readln(a,b,c);

maxmin(a,b);

maxmin(a,c); {a=max}

maxmin(b,c); {c=min}

writeln(a,b,c);

end.
13. Если среди чисел sin(x ⁿ) (n = 1, 2, ... ,30) есть хотя бы одно отрицательное число, то логической переменной t присвоить значение true, а иначе – значение false.
var y,x : real;

n : integer;

t : boolean;

begin

write('Введите значение x –');

readln(x);

y:=1; n:=0;

repeat

n:=n+1; y:=x*y; t:=sin(y)<0

until t or (n=30);

writeln(t);

end.
14. Определить k – количество трехзначных натуральных чисел, сумма цифр которых равна n (1
var d1, d2, d3, k, n : integer;

begin

writeln('Введите число n, с которым будем сравнивать сумму цифр числа');

readln(n);

k:=0;

{d1 – левая, d2 – средняя, d3 – правая цифры числа}

for d1:=1 to 9 do

for d2:=0 to 9 do

for d3:=0 to 9 do

if d1+d2+d3=n then begin

k:=k+1; write(d1,d2,d3, ' ');

end;

writeln('Количество искомых чисел равно –', k);

end.
Варианты заданий

Вариант 1	Задача 1 Найти знакочередующуюся сумму цифр числа n (пусть запись числа n в десятичной системе есть ak ak – 1 ... a0; найти (–1)k * ak + … + a2 – a1 + a0 ). Вводите число n как значение типа integer. Например, если n = 1234, то ответ равен –1 + +2 – 3 + 4 = 2. Строки не использовать. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 2 Дана последовательность из n целых чисел. Определите количество чисел в наиболее длинной последовательности из подряд идущих нулей. Например, если n=10 и вводим числа 1, 0, 0, 3, 5, 0, 0, 0, 2, 0, то ответ равен 3. Задача 3 Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа n. Вводите число n как значение типа integer. Например, если n = 1234, то ответ равен 4321. Строки не использовать. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19.
Вариант 2	Задача 1 Дана последовательность из не менее чем двух натуральных чисел, за которой следует 0. Вычислите сумму тех из них, порядковые номера которых – простые числа. Например, если вводили 1, 12, 8, 4, 50, 6, 77, 8, 9, 0, то номера выделенных чисел являются простыми числами (2, 3, 5, 7) и ответ равен 12 + 8 + 50 + 77 = 147. Подсказка: используйте булевскую функцию для проверки, является номер простым числом или нет. Задача 2 Даны целое n>2 и вещественные числа a1, b1, ..., an, bn (ai < bi). Рассматривая пары ai и bi как левые и правые концы отрезков на одной и той же прямой, определить концы отрезка, являющегося пересечением всех этих отрезков. Если такого отрезка нет, сообщить об этом. Например, если n=3 и a1 = 0, b1= 10, a2 = 1, b2 = 11, a3 = –1, b3 = 5, то результатом будет отрезок [1, 5]. Задача 3 В заданной последовательности чисел длиной n определить длину самой большой упорядоченной по возрастанию подпоследовательности соседних элементов. Например, если вводили 1, 12, 8, 4, 50, 6, 22, 77, 8, 9, 0, то ответ равен 3 (это длина подпоследовательности 6, 22, 77).
Вариант 3	Задача 1 Даны целое n>0 и целые числа a1, a2, ..., an. Определить, сколько чисел последовательности a1, a2, ..., an принимает наибольшее значение. Например, в последовательности 2,5,7,4,7,6,0 наибольшее значение 7 встречается 2 раза. Задача 2 Не используя стандартные функции, вычислить с точностью eps>0 … Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новые числитель и знаменатель через предыдущие значения. Задача 3 Составьте программу, которая в записи натурального числа N меняет местами крайние цифры, т.е. из 451 получает 154. Вход и выход должны быть значениями типа integer. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19.
Вариант 4	Задача 1 Даны натуральные числа n, m. Получить сумму m последних цифр числа n. Число n вводить как величину типа integer и строки не использовать. Пример. Пусть n = 12345, m=3, тогда ответ равен 3+4+5 = =12. Подсказка. Как получать цифры целого числа, учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 2 Не используя стандартные функции, вычислить с точностью eps>0 … Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новый числитель через предыдущее значение. Задача 3 Известно, что любое натуральное число N > 7 можно представить в виде N = 3N1 + 5N2 (N1 и N2  0). Напишите программу нахождения всех пар N1 и N2 для числа N. Например, для числа 16 такая пара единственная N1 = 2 и N2 = 2.
Вариант 5	Задача 1 Даны целое n>0 и вещественные числа x1, x2, ..., xn. Определить, сколько из них больше своего предыдущего числа. Задача 2 Не используя стандартные функции, вычислить с точностью eps>0 … Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новый числитель через предыдущее значение. Задача 3 Определить функцию f(n), значением которой является натуральное число, получаемое выбрасыванием из записи натурального числа n первой справа цифры 0 или 5. Например, f(13510) = 1351, f(1351) = 131. Для данного натурального числа m, примените функцию f последовательно необходимое число раз, так чтобы в записи m не осталось цифр 0 и 5. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19.
Вариант 6	Задача 1 Даны натуральное n и вещественные числа x1, y1, x2, y2,…, xn, yn. Рассматривая пары xi, yi как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки. Задача 2 Дано натуральное n>0. Найти произведение первых n простых чисел. Подсказка: используйте булевскую функцию для проверки, является число простым числом или нет. Задача 3 Определите функцию f без параметров, в теле которой вводятся ненулевые целые числа, до тех пор, пока не введется 0. Значением функции является число перемен знаков у членов введенной последовательности (например, в последовательности 1, –34, 8, 14, –5 знак меняется 3 раза).
Вариант 7	Задача 1 Даны целое n>0 и последовательность из n вещественных чисел, среди которых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел последовательности. Задача 2 var a,b:real; t:boolean; Переменной t присвоить значение true, если уравнения x2 + +6.2x + a2 = 0 и x2 + ax + b – 1 = 0 имеют вещественные корни и при этом оба корня первого уравнения лежат между корнями второго, и присвоить значение false во всех остальных случаях. Задача 3 Даны длины a, b и c сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Замечание: длина медианы, проведенной к стороне a, равна 0,5 * . Определите функцию для вычисления медианы и используете ее необходимое число раз.
Вариант 8	Задача 1 Найти все целые корни уравнения ax3 + bx2 + cx + d = 0, где a, b, c, d – заданные целые числа, причем a<>0 и d<>0. (Замечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d). Задача 2 Дано: натуральное n, действительные a 1, a 2,...,a n. Вычислить: a1 + a2 * (a2 –1) + a3 * (a3 –1) * (a3 – 2) + a4 * (a4 – 1) * * (a4 – 2) * (a4 – 3) + ... + an * (an – 1) * (an – 2) *...* (an – n +1). Задача 3 Найти все натуральные четырехзначные числа, не превосходящие заданного N, цифры в которых образуют строго возрастающую последовательность (1000  N < 10000).
Вариант 9	Задача 1 Пусть n – натуральное число. Обозначим через n!! произведение 1 * 3 * ... * n для нечетного n и 2 * 4 * 6 * ...* n для четного n. Дано натуральное n. Получить n!!. Задача 2 Даны не менее трех различных натуральных чисел, за которыми следует 0. Определить три наибольших числа среди них (должно выполняться max1  max2  max3). Подсказка. Введите первые три числа в переменные a1, a2 и a3. Присвойте эти значения как начальные для переменных max1, max2, max3, чтобы выполнялось соотношение max1   max2  max3). Затем вводите остальные числа и на каждом шаге осуществляйте необходимую коррекцию max1, max2, max3. Задача 3 С помощью подпрограммы-функции получить значения для данных M, x.
Вариант 10	Задача 1 Даны действительные числа x, a, натуральное n. Вычислить: . n скобок Задача 2 Дано n вещественных чисел. Найти порядковый номер того из них, которое наиболее близко к квадрату какого-нибудь целого числа. Например, если n=10 и вводим числа 110, 90, 80, 30, 50, 40, 40, 30, 22, 60, то ответ равен 3 или 5 (имеем |80 – 92| = | 50 – 72| = 1). Подсказка: определите функцию f(k), которая вычисляет абсолютную величину разности k и ближайшего целого квадрата (ближайшим целым квадратом будет (trunc( ))2 или (trunc( )+1)2). Задача 3 Дано натуральное n. Вычислить: .
Вариант 11	Задача 1 Даны натуральное число n, действительные числа x 1 , x 2 , ..., x n (n >= 3). Вычислить: (x1 + 2 * x2 + x3) * (x2 + 2 * x3 + +x4) * ...* (xn – 2 + 2 * xn – 1 + xn). Задача 2 Даны действительные числа x1, y1, x2, y2, x3, y3. Находится ли точка с кординатами (x,y) внутри треугольника с вершинами (x1, y1), (x2, y2), (x3, y3)? Подсказка: соедините точку (x,y) с вершинами треугольника; рассмотрите площади четырех треугольников. Определите функции для вычисления длины отрезка и площади треугольника и используйте эти функции. Задача 3 Вычислить бесконечную сумму с заданной точностью E (E>0). . Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем Е; это и все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: вместо вычисления факториала вычисляйте величину, обратную факториалу, тем самым вы избежите целочисленного переполнения (см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.20, задача 3).
Вариант 12	Задача 1 Числа Фибоначчи: F0 = 0, F1 = 1, а любое следующее число Фибоначчи равно сумме двух предыдущих: Fn = Fn – 1 + Fn – 2. Известно, что при достаточно больших n справедливо приближенное равенство . Определите наименьший номер n, начиная с которого равенство выполняется с точностью до заданного eps. Задача 2 Вычислить . Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новые числитель и знаменатель через предыдущие значения. Задача 3 День года задан в виде пары целых чисел (m, d), где m – месяц (1m12), d – день (1d31). Программа сначала определяет, правильная ли это дата, и выдает число n, равное 1, 2, …, 6 или 7 в зависимости от того, на какой день недели (понедельник, вторник,…, субботу или воскресение) приходится этот день. Считаем, что год – невисокосный и 1 января – понедельник.
Вариант 13	Задача 1 Рассмотрим последовательность e 1, e 2, e 3,..., образованную по следующему закону e k = , k = 1,2,.... Дано действительное eps. Найти первый член e n этой последовательности, для которого |en – en–1| < eps. (Существование en гарантируется одной из теорем математического анализа: чем меньше eps, тем ближе en к числу е = =2,718281828....). Задача 2 Определите, сколько шестизначных чисел чисел имеют одинаковые суммы трех первых и трех последних цифр («счастливые билеты»). Задача 3 Вычислить число , перемножив n сомножителей произведения Валлиса:
Вариант 14	Задача 1 Определите функцию f(n), n – натуральное число, равную сумме цифр числа n. Исследуйте, есть ли среди чисел < m такие n, что (f(n))2 = n. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 2 Даны натуральные n, m. Получить все меньшие n натуральные числа, сумма цифр которых равна m. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 3 Вычислить число , учитывая n членов ряда Грегори:
Вариант 15	Задача 1 Дано натуральное n. Вычислить: . n корней Задача 2 Вычислить Задача 3 Пусть дано натуральное число n. Составить программу вычисления n3 как суммы нечетных чисел, исходя из того, что: 13=1; 23 = 3+5; 33=7+9+11; 43 = 13+15+17+19; 53 = =21+23+25+27+29; …
Вариант 16	Задача 1 Даны натуральные числа m и n. Найти такие натуральные p и q, не имеющие общих делителей, что p/q = m/n. Задача 2 Даны натуральное n и целые числа c1, c2, … , cn. Имеются ли в последовательности c1, c2, … , cn: а) два идущих подряд нулевых члена; б) три идущих подряд нулевых члена? Задача 3 Вычислить с точностью eps>0 бесконечную сумму Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать.
Вариант 17	Задача 1 Даны натуральное число n и целые числа a1, a2,…, an. Найти наибольшее из нечетных чисел и количество четных чисел, входящих в последовательность a1, a1+1, a2, …, an. Задача 2 Даны натуральное число n, действительные числа x1, x2, …, xn, xn+1, …, x2n. Вычислить сумму чисел из xn+1, …, x2n, которые превосходят по величине все числа x1, x2, …, xn. Задача 3 Вычислить с точностью eps>0 бесконечную сумму Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать.
Вариант 18	Задача 1 Даны натуральное n и целые числа c1, c2, … , cn. Имеются ли в последовательности c1, c2, … , cn три идущих подряд нулевых члена? Задача 2 Даны натуральное число n и натуральные числа x1, x2, …, xn. Найти номер последнего простого числа в последовательности x1, x2, …, xn; если простых чисел нет, то ответом должно быть число n+1. Подсказка: используйте булевскую функцию для проверки, является число простым числом или нет. Задача 3 Составить программу вычисления значения функции Z(x) =
Вариант 19	Задача 1 Вводим вещественные числа x1, x2, … до тех пор, пока не введем отрицательное число (первое число  неотрицательное). И пусть x1, x2, …, xn – члены данной последовательности, предшествующие отрицательному числу. Посчитать количество полных квадратов среди чисел x1, x2, …, xn. Подсказка. Число k является полным квадратом, если выполнено равенство k = (trunc( ))2. Задача 2 Даны натуральное число n и действительные числа x1, x2, …, xn. Выяснить, какое число встречается в последовательности x1, x2, …, xn раньше – положительное или отрицательное. Если все члены последовательности равны нулю, то сообщить об этом. Задача 3 Составить программу вычисления значения функции Z(x) =
Вариант 20	Задача 1 Даны натуральное число n, действительные числа x1, x2, …, xn. Найти длину наименьшего отрезка числовой оси, содержащего все числа x1, x2, …, xn. Задача 2 Даны натуральное число n и натуральные (большие 0) числа x1, x2, …, xn. Выяснить, какое число встречается в последовательности x1, x2, …, xn раньше – составное или простое. Если все члены последовательности равны 1, то сообщить об этом. Подсказка: используйте булевскую функцию для проверки, является число простым числом или нет. 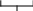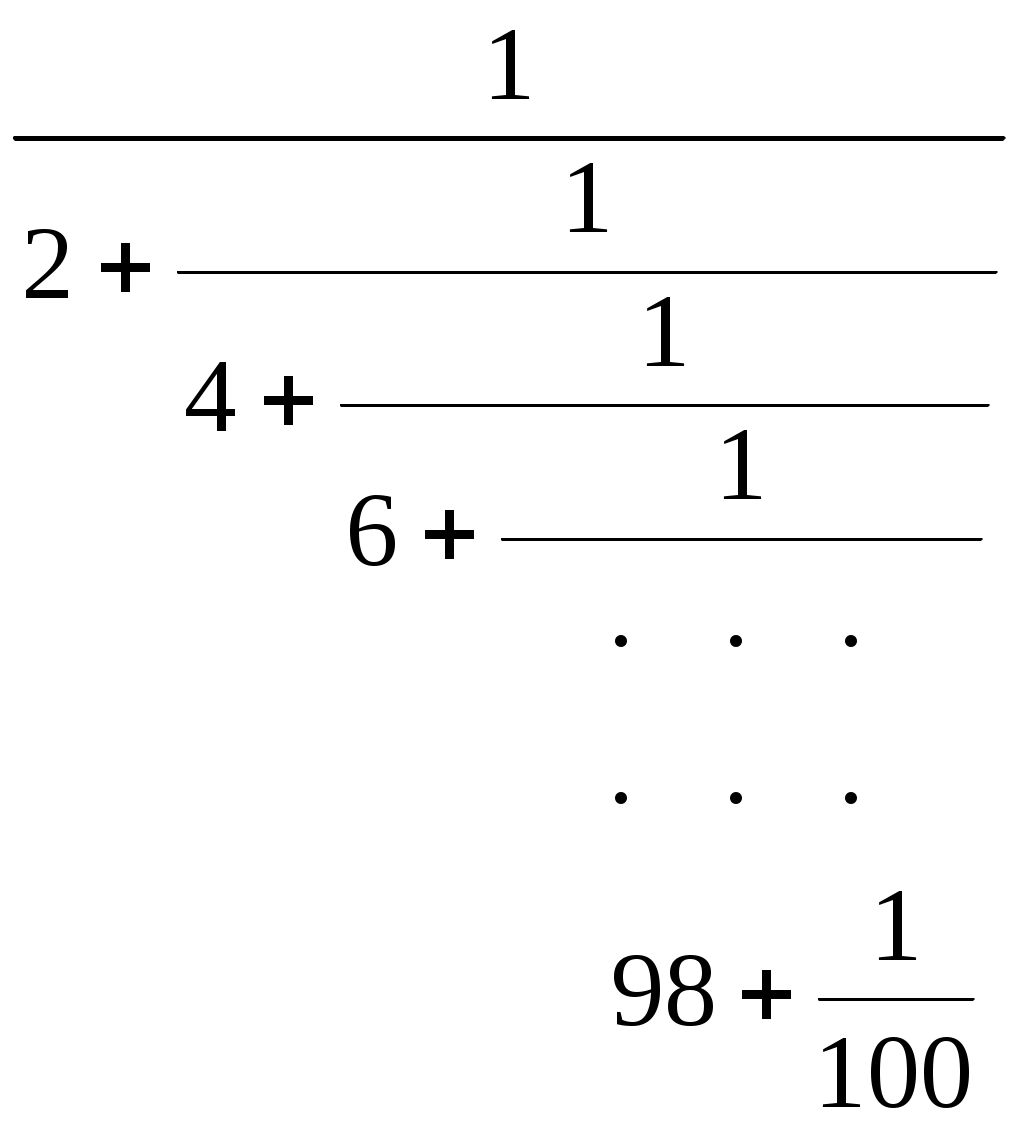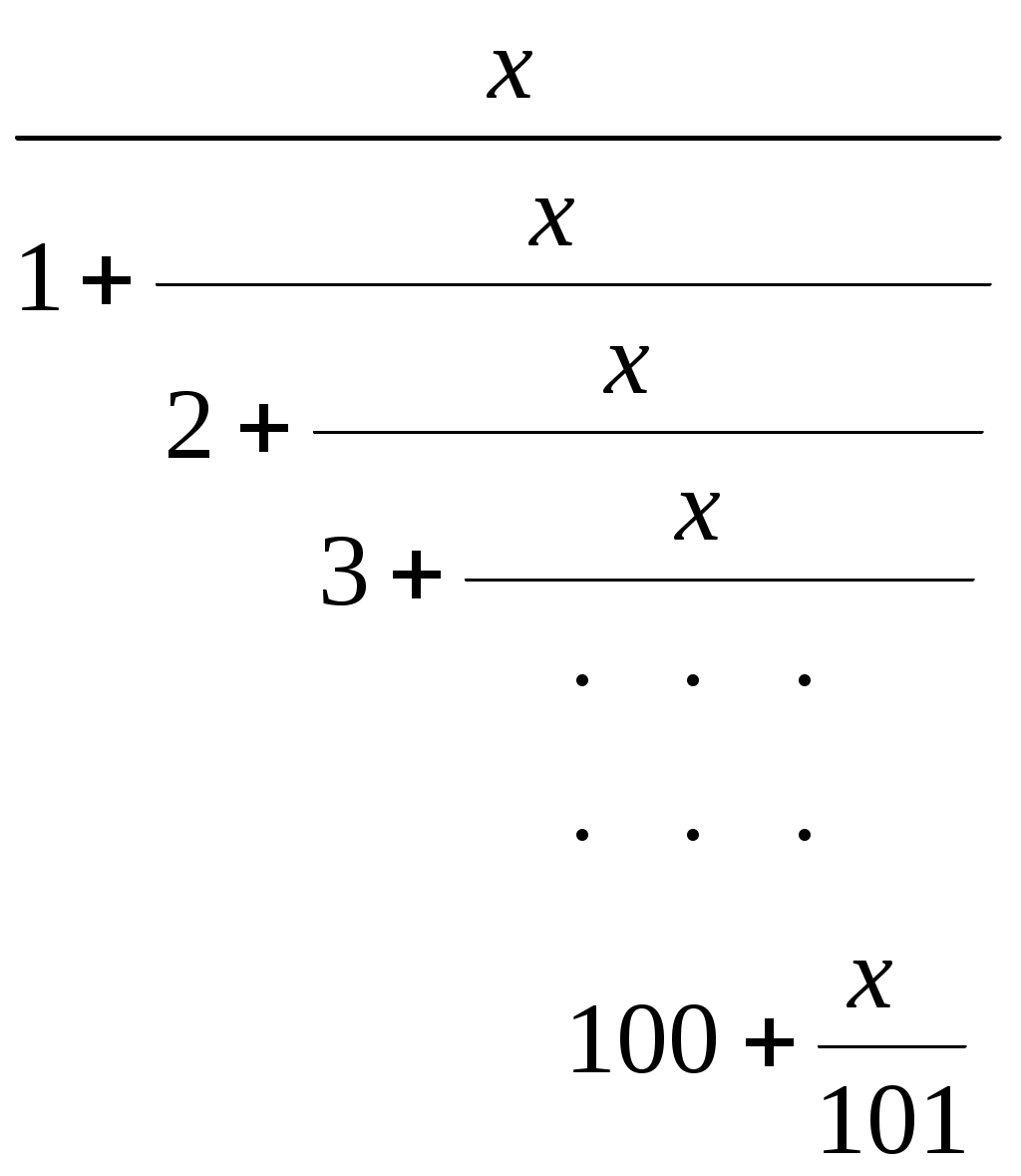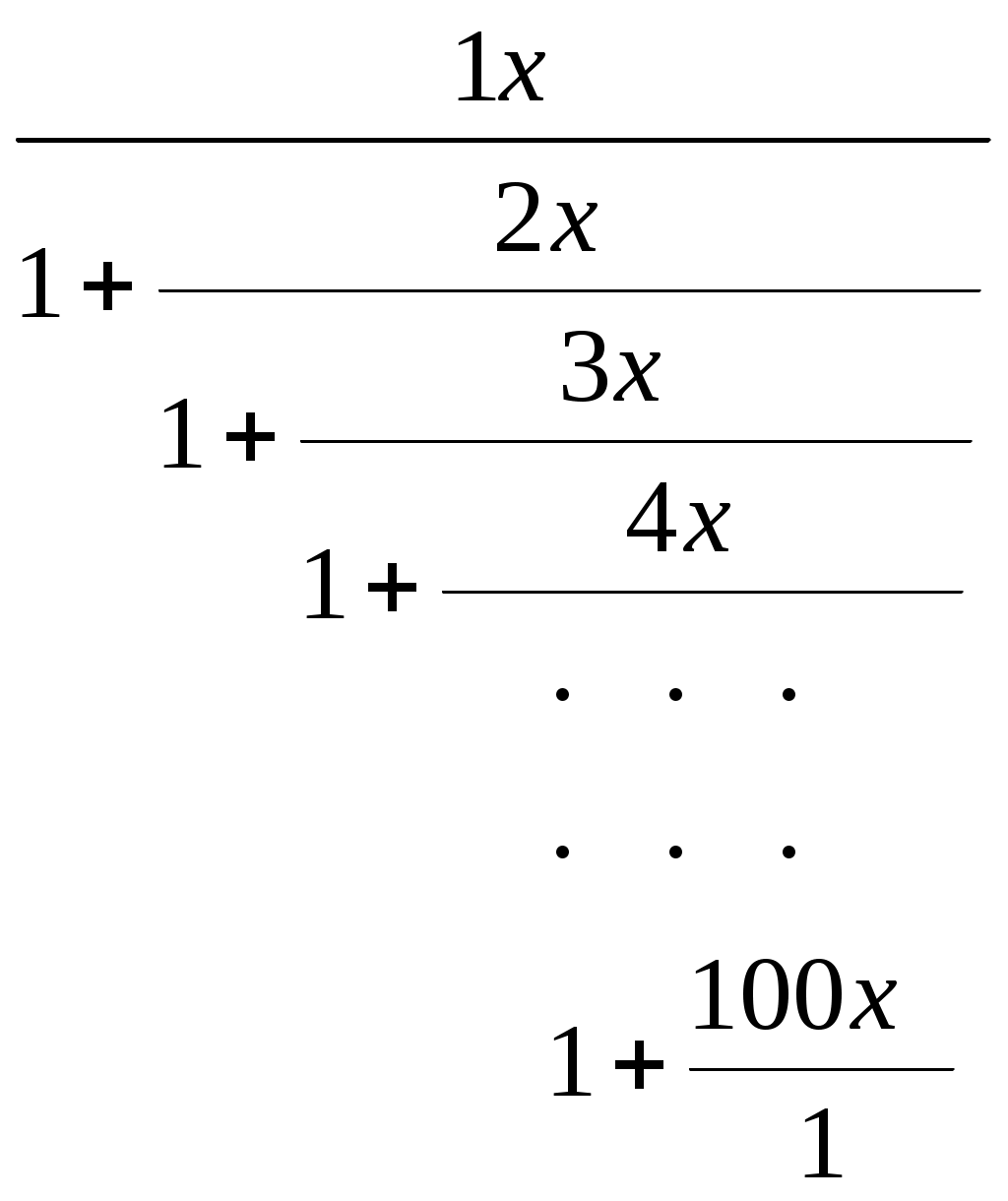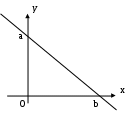Задача 3 Д аны вещественные a>0, b>0. Напишите функцию f(a,b), которая считает, сколько точек с целочисленными координатами (x,y) находится в треугольнике. Если точка попадает на сторону треугольника, то она должна тоже учитываться. Например, f(1,1) = 3.

  1   2   3