Физика Контрольная работа. Фізика КР. Контрольна робота з дисципліни Фізика Виконав студент 3 курсу факультету групи Перевірив викладач 2015

• Название: Контрольна робота з дисципліни Фізика Виконав студент 3 курсу факультету групи Перевірив викладач 2015
• Анкор: Физика Контрольная работа
• Дата: 25.03.2022
• Размер: 120.5 Kb.
• Имя файла: Фізика КР.doc
• Тип: Контрольна робота; #416316

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ


Контрольна робота

з дисципліни

«Фізика»
Виконав:

студент 3 курсу

факультету

групи

Перевірив:

викладач

2015
Зміст

Задача 1 3

Задача 2 3

Задача 3 4

Задача 4 4

Задача 5 5

Задача 6 6

7

Задача 7 7

Список використаної літератури 8

Задача 1

Знайти власний час життя нестабільної частинки   - мезона, що рухається зі швидкістю 0,99 c (с – швидкість світла у вакуумі), якщо відстань, яку він пролітає до розпаду, дорівнює приблизно 10 км.
Розв’язання

Дано: ν = 0,99 c S=10 км

∆τ0  - ?

Власний час життя мю-мезона ∆τ визначається формулою:


c = 3·10⁸ м/с, v – швидкість руху мю-мезона,

∆τ – час життя мю-мезона для земного спостерігача:

∆τ = S/v.

Розраховуємо:

Відповідь: Власний час життя мю-мезона становить 1,4·10^-5 с

Задача 2

Обчислити середню довжину вільного пробігу молекул повітря при тиску 1·10³ Па та температурі 10ºС.
Розв’язання

Дано: p = 1·105 Па t = 10ºС

- ?

Середня довжина вільного пробігу знаходиться за формулою

(1)

де

d = 3·10^-10 м– ефективний діаметр молекул повітря

n – концентрація молекул

Із формули для тиску р = n k T знайдемо концентрацію і, підставивши у формулу (1), отримаємо:

k = 1,3810^–23 Дж/К – стала Больцмана;

Т- абсолютна температура.

T = t +273 = 10 + 273 = 283К

Розраховуємо:

.

Відповідь: 

Задача 3

Визначити заряд, що пройшов резистором  за 10 с, якщо сила струму в резисторі за цей час рівномірно зростала від 0 до 5 А.
Розв’язання

Дано t = 10 c I0 = 0 A I0 = 5 A

q - ?

По визначенню сила струму:

При рівномірному збільшенні струму маємо лінійну залежність і тоді:



В розрахунку беремо середнє значення струму:



Відповідь: q = 25 Кл.

Задача 4

Прямой проводник согнутый в виде прямоугольника

Прямий провідник зігнутий у вигляді прямокутника з сторонами довжиною 0,2 м і 0,3 м. Струм якої сили потрібно пропустити цим провідником, щоб напруженість поля у точці перетину діагоналей була 19 А/м. Розв’язання пояснити малюнком.
Розв’язання

Дано a = 0,2 м b = 0,3 м E=19 А/м

I - ?

Индукция поля отрезка проводника с током:

Откуда напряжённость:


Тогда в нашем случае:



где   и   - напряжённости магнитного поля от нижних и верхних и правых и левых проводников соответственно.
I=(B/2μ₀)*(πab/c)
c= √a²+b²

Задача 5

Тіло масою 100 г здійснює гармонічні коливання за законом S=0,2sin(10t+/2). За який час кінетична енергія тіла зменшиться від 2 Дж до 1 Дж?

Розв’язання

Дано m = 100 г S=0,2sin(10t+/2) E1 = 2 Дж E2 = 1 Дж

t - ?

ПРИКЛАД 1. Матеріальна точка здійснює гармонічні коливання з періодом 0.5 с. Амплітуда коливання 80 см. Рух точки починається з положення х₀ =30 см. Написати рівняння руху точки. Знайти залежність від часу швидкості і прискорення. Знайти максимальну швидкість точки і її максимальне прискорення.

Дано А = 80 см Т = 0.5 с х0 =40 см	СІ 0.8 м 0.4 м
x(t), v(t),a(t)- ? vm, am - ?

Розв’язання
Запишемо рівняння руху в загальному вигляді

.

При t = 0 зміщення точки з положення рівноваги

.

Знайдемо частоту коливань

.

Тоді рівняння має вид

м.

По визначенню швидкості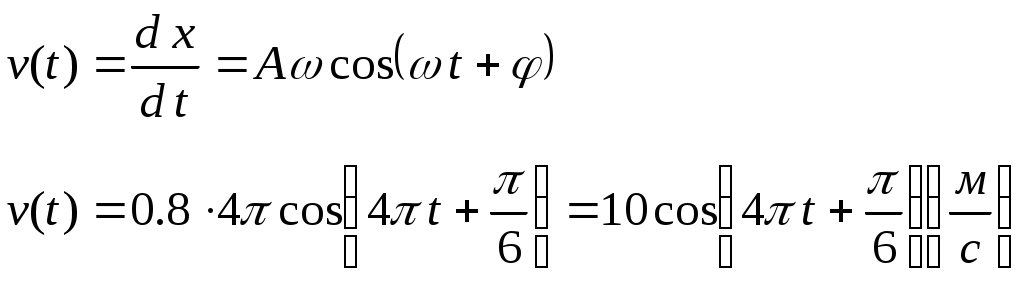



Максимальна швидкість .

.

Задача 6

Яку різницю довжин хвиль може «розрізнювати» дифракційна решітка у спектрі другого порядку для фіолетових променів (довжина хвилі 0,4 мкм), якщо період решітки дорівнює 2 мкм, ширина її 2 см.

Розв’язання

Дано n = 50 l = 1 мм = 10-3м kmax=2 λ = 400 нм = 4·10-7 м φ - ?

Умова максимумів:

, звідки:

Задача 7

Використовуючи співвідношення невизначеностей, показати , що в ядрі не можуть знаходитися електрони. Лінійні розміри ядра прийняти такими, що дорівнюють 5,8·10-15 м. Врахувати, що питома енергія зв’язку в середньому дорівнює 8 МеВ/нуклон.

Розв’язання
Дано:

l = 5,8·10^-15 м

 = 8 МеВ/нуклон




Із відношення невизначеностей Гейзенберга:

Δx Δр ≥ h (1)

h = 6,63·10^-34 Дж·с – стала Планка

Δр - невизначеність у знаходженні імпульсу.

З (1) Δр ≥ h/Δx або Δр ≥ h/ l, l – орієнтовний розмір ядра

Вважаємо, що p > Δр, тоді p > h / l.

Тут - релятивістський випадок

с = 3·10⁸ м/с – швидкість світла у вакуумі

Т. як T >> E₀, то і T_min= сh/ l = 3·10⁸·6,63·10^-34/(5,8·10^-15) = 3,4·10^-11 Дж

За умовою:  = 8 МеВ=8·10⁶·1,6·10^-19 Дж = 1,28·10^-12 Дж

Отримане значення T_min значно більше, ніж питома енергія зв’язку на кулон у ядрі, тобто перебування електронів у ньому неможливе.

Список використаної літератури

1. 
   Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики. Т.1. Механіка. Молекулярна фізика і термодинаміка. –К, 1999.–532 с.
   
2. 
   Савельев И.В. Курс общей физики: В 3 т. Т.1. Механика. Молекулярная физика.– М., 1987.– 416 с.
   
3. 
   Фирганг Е.В. Руководство к решению задач по курсу общей физики. – М, «Высшая школа», 1977.