Главная страница
Навигация по странице:

  • 1,25 с; 3,5 м/с; 0,4 м/с

  • 44,7 м

  • 44 м/с

  • 2,03 м/с

  • 3 м/с

  • 12 м/с

  • 1,52 с

  • 6 м/с

  • 2,4 рад/с

  • 13,2 рад/с; 8,2 рад/с

  • 1,1 м/с

  • 0,8 м/с

  • 4 рад/с; 6 рад/с

  • 3,3 рад/с

    		•

    док. І. механiка кінематика матеріальної точки та поступального руху тіл. Основнi формули


    Скачать 409 Kb.
    НазваниеІ. механiка кінематика матеріальної точки та поступального руху тіл. Основнi формули
    Дата05.01.2021
    Размер409 Kb.
    Формат файлаdoc
    Имя файлаdoc1 (3).doc
    ТипДокументы
    #165996
    страница1 из 4
      1   2   3   4

    І. МЕХАНIКА
    1. Кінематика матеріальної точки та

    поступального руху тіл.
    Основнi формули
    1. Кiнематичнi рiвняння руху в координатнiй формi

    x = x(t); y = y(t); z = z(t).

    2. Кiнематичне рiвняння в природній формi

    s = s(t),

    деs – шляхова координата

    3. Проекцiї швидкостi на координатнi осi



    4. Величина (модуль) миттєвої швидкості



    5. Рівняння (формупа) шляху

    S = S(t).

    6. Миттєва швидкiсть



    7. Шлях, пройдений тілом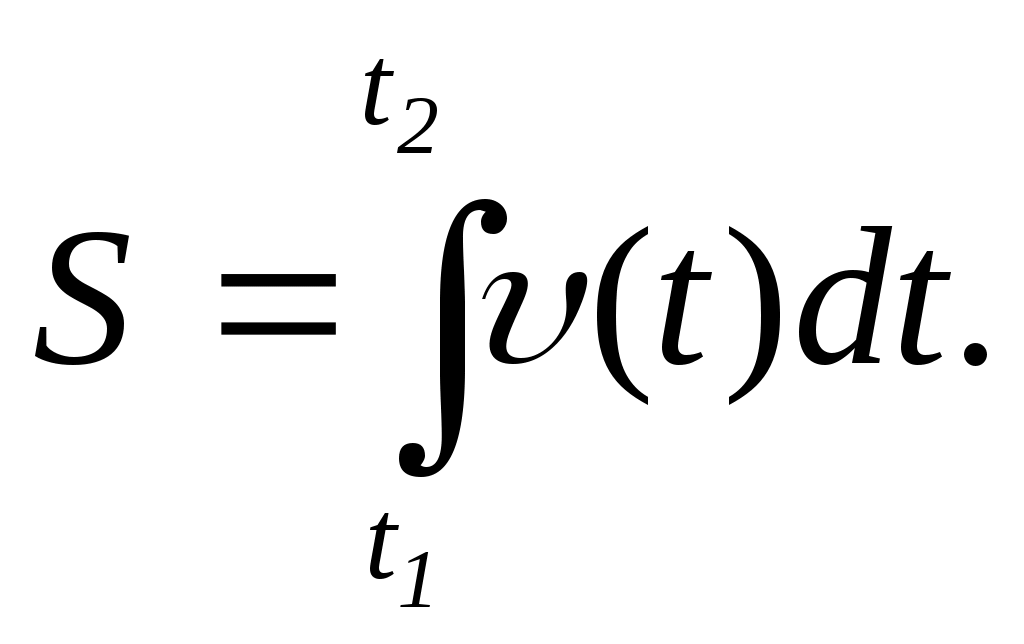



    8. Середня швидкість руху



    9. Проекцiї прискорення на осi координат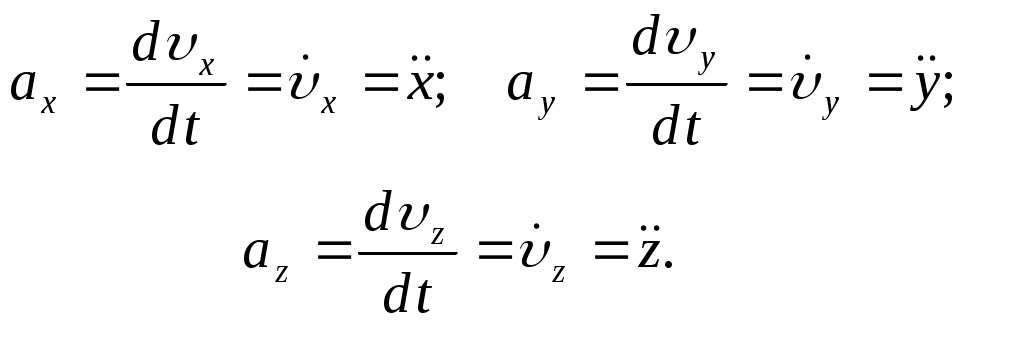


    10. Величина (модуль) прискорення



    11. Величина (модуль) тангенцiальної складової прискорення



    12. Величина (модуль) нормальної складової прискорення



    де R – радіус кривини траєкторії.

    13. Величина (модуль) повного прискорення



    14. Середнє прискорення



    15. Кiнематичне рiвняння рiвномiрного прямолiнiйного руху



    16. Кiнематичне рiвняння рiвнозмiнного прямолiнiйного руху





    1. Два автомобілі рухаються по двох прямолінійних і взаємно перпендикулярних дорогах в напрямках до перехрестя зі сталими швидкостями v1 = 100 км/год. і v2 = 50 км/год. Перед початком руху перший автомобіль перебував на відстані S1 = 50 км від перехрестя, другий на відстані S2 = 100 км. Через скільки часу після початку руху відстань між автомобілями буде мінімальною? (0,8 год.)

    2. Рухи двох матеріальних точок задаються рівняннями: x1 = A1 + B1t + C1t2, x2 = A2 + B2t + C2t2, де A1 = 10 м, B1 = 4 м/с, C1 = -0,2 м/с2, A2 = 1 м, B2 = 2 м/с, C2 = 0,6 м/с2. В який момент часу t швидкості цих точок будуть однаковими? Визначити швидкості v1 і v2 та прискорення α1 і α2 точок у цей момент. (1,25 с; 3,5 м/с; 0,4 м/с2, 1,2 м/с2)

    3. Дві матеріальні точки рухаються згідно з рівняннями: x1 = A1 + C1t2 + D1t3, x2 = B2t + C2t2 + D2t3, де A1 = 2 м, C1 = 23 м/с2, D1 = -1 м/с3, B2 = 4 м/с, C2 = 11 м/с2, D2 = 1 м/с3. В який момент часу прискорення цих точок будуть однакові? Визначити швидкості точок у цей момент часу. (2 с; 80 м/с; 60 м/с)

    4. Одночасно з одного і того ж пункту в одному напрямку починають рухатись прямолінійно два автомобілі. Залежність пройденого шляху від часу визначається рівняннями: S1 = C1t2, S2 = C2t2 + D2t3, де C1 = 3 м/с2, C2 = 5 м/с2, D2 = 3 м/с3. Визначити відносну швидкість автомобілів у момент часу t = 2 с.(44 м/с)

    5. Залежність пройденого тілом шляху від часу описує рівняння S = Ct2 + Ht4, де С = -9 м/с2, Н = 0,25 м/с4. Визначити екстремальне значення швидкості тіла. (29,4 м/с)

    6. Ракета, встановлена в момент старту на висоті Н0 = 5 м над поверхнею Землі, рухається вгору з прискоренням, яке з часом змінюється за законом α = kt2, де k = 1,5 м/с4. На якій висоті над поверхнею Землі буде ракета через час t = 6 с після старту? (167 м)

    7. Залежність швидкості тіла від часу задається рівнянням v = A + Bt + Ct2, де А = 4 м/с, В = 2 м/с2, С = 0,3 м/с3. Який шлях проходить тіло за проміжок часу від t1 = 2 с до t2 = 5 с? Яка середня швидкість <v> тіла і середнє прискорення <α> за цей проміжок часу? (44,7 м; 14,9 м/с; 3,1 м/с2)

    8. Залежність швидкості тіла від часу визначається рівнянням v = A + Bt, де А = 3 м/с, В = 4 м/с2. Який шлях проходить тіло за проміжок часу від t1 = 0 с до t2 = 4 с? Визначити середню швидкість <v> тіла за цей проміжок часу. (44 м; 11 м/с)

    9. М’яч кинули з підвищення в горизонтальному напрямку зі швидкістю v0 = 20 м/с. Визначити швидкість v, тангенціальне ατі нормальне αn прискорення м’яча через час t = 4 с після початку руху. (44 м/с; 8,73 м/с2; 4,45 м/с2)

    10. Точка рухається по колу зі швидкістю v = Bt, де В = 0,75 м/с2. Після початку руху вона проходить шлях, рівний 0,2 довжини кола. Визначити повне прискорення α точки у цей момент часу. (2,03 м/с2)

    11. Нормальне прискорення точки, що рухається по колу радіусом R = 4 м, змінюється за законом αn = A + Bt + Ct2, де А = 1 м/с2, В = 3 м/с3, С = 2,25 м/с4. Визначити тангенціальне прискорення ατ точки, шлях, що пройшла точка за час t1 = 6 с після початку руху, повне прискорення α у момент часу t2 = 2/3 с. (3 м/с2; 66 м; 5 м/с2)

    12. Рух матеріальної точки в площині xy описується рівнянням x = At, y = At + Bt2, де А = 0,5 м/с, В = -1 м/с2. Отримати рівняння траєкторії матеріальної точки y(x), швидкість v точки в момент часу t1 = 0,5 с, прискорення α точки, момент часу t2, коли кут між швидкістю і прискоренням α = π/4. (y = 0,5 + 4x2; 1,6 м/с; 2 м/с2; 0,5 с)

    13. Рівняння руху матеріальної точки мають вигляд: x = A1 + B1t, y = B2t + C2t2, z = 0, де А1 = -9 м, В1 = 3 м/с, В2 = 4 м/с, С2 = -1 м/с2. Визначити швидкість v, прискорення α та кут γ між векторами цих величин у момент часу, коли координата y має екстремальне значення. (3 м/с; 2 м/с2; 900)

    14. Рівняння руху матеріальної точки мають вигляд: x = B1t + D1t3, y = B2t + C2t2, z = 0, де В1 = 27 м/с, D1 = -1 м/с3, B2 = 32 м/с, C2 = -8 м/с2. Визначити тангенціальне ατ , нормальне αn прискорення і радіус кривини R траєкторії в момент часу t1, коли координата y приймає екстремальне значення і в момент t2, коли таке значення приймає координата x. (12 м/с2; 16 м/с2, 14 м; 16 м/с2; 18 м/с2; 14,2 м)

    15. Рух матеріальної точки по колу радіусом R = 2 м описується рівнянням S = A + Ct2, де А = 4 м, С = -1 м/с2. Визначити момент часу t, коли нормальне прискорення точки дорівнює αn = 8 м/с2. Знайти швидкість v, тангенціальне ατ і повне α прискорення точки в цей момент часу. (2 с; 4 м/с; 2 м/с2; 8,2 м/с2)

    16. Залежність шляху від часу для точки, що рухається по колу радіусом R = 3 м, дається рівнянням S = Dt3, де D = 0,01 м/с3. Визначити момент часу t, коли лінійна швидкість точки v = 3 м/с. Знайти нормальне αn, тангенціальне ατ і повне α прискорення точки в цей момент часу. (10 с; 3,0 м/с2; 0,6 м/с2; 3,1 м/с2)

    17. Матеріальна точка починає рухатися за годинниковою стрілкою по колу радіусом R = 0,2 м із сталим тангенціальним прискоренням ατ = 0,15 м/с2. Через який час t вектор прискорення α утворить з вектором швидкості v кут α= 600? Який шлях пройде за цей час рухома точка? (1,52 с; 0,17 м)

    18. Матеріальна точка рухається по колу радіусом R = 9 м. В момент часу, коли вектори повного α і нормального αn прискорень утворюють кут α = 600, нормальне прискорення точки αn = 4 м/с2. Визначити швидкість v і тангенціальне ατ прискорення точки. (6 м/с; 6,9 м/с)



    2. Кінематика обертального руху твердого тіла.
    Основнi формули


    1. Кiнематичне рiвняння обертального руху



    1. Миттєва кутова швидкiсть



    1. Середня кутова швидкiсть



    1. Величина (модуль) кутового прискорення



    1. Кiнематичне рiвняння рiвномiрного обертального руху



    1. Перiод обертання



    1. Частота обертання



    1. Лiнiйна швидкiсть



    1. Тангенцiальне прискорення



    1. Нормальне прискорення





    1. Шків радіусом R1 = 15 см сполучений ремінною передачею зі шківом радіусом R2 = 10 см. Частота обертання першого шківа n1 =10 об/с. Визначити частоту n2 обертання другого шківа. (15 об/с)

    2. Маховик, обертаючись рівноприскорено, збільшив за час t = 2 с частоту обертання від n1 = 4 об/с до n2 = 14 об/с. Визначити кутове прискорення маховика і число обертів N, які він здійснив за час t. (31,4 рад/с²; 18 обертів)

    3. Маховик, який обертався з частотою n1 = 16 об/с, при гальмуванні почав обертатися рівносповільнено і виконав N = 314 обертів. Коли гальмування припинили, частота обертання маховика стала n2 = 4 об/с. Визначити кутове прискорення маховика і час t, протягом якого здійснювалось гальмування. (2,4 рад/с2; 31,4 с)

    4. Якір електродвигуна обертається з частотою n0=50 об/с. Після вимкнення струму якір почав рухатися рівносповільнено і до зупинки зробив N = 1570 обертів. Визначити кутове прискорення якоря. (5 рад/с)

    5. Колесо обертається згідно з рівнянням φ = А + Вt + Сt2 + Dt3, де А = 1 рад, В = 4 рад/с, С = 0,5 рад/с2, D = 0,6 рад/с3. Визначити кутову швидкість і кутове прискорення в момент часу t = 2 с, середню кутову швидкість <> і середнє кутове прискорення <> за проміжок часу від t1 = 2 c до t2 = 4 c. (13,2 рад/с; 8,2 рад/с2; 23,8 рад/с; 11,8 рад/с2)

    6. Диск радіусом R = 4 см обертається навколо нерухомої осі так, що залежність кутової швидкості від часу задається рівнянням = Аt + Dt4, де А = 2 рад/с2, D = 0,5 рад/с3. Визначити повне прискорення α точок на ободі диска в момент часу t = 2 с після початку руху і число обертів N, виконаних диском. (5,8 м/с²; 1,15 обертів)

    7. Колесо обертається навколо нерухомої осі так, що кут його повороту залежить від часу як φ = Ct2, де С = 0,7 рад/с2. У момент часу t = 1,5 с лінійна швидкість точки на ободі колеса v = 0,5 м/с. Визначити повне прискорення α цієї точки. (1,1 м/с2)

    8. Тіло обертається навколо нерухомої осі за законом φ = А + Вt + Ct2, де А = 5 рад, В = 8 рад/с, С = -1 рад/с2. Визначити повне прискорення точки, яка знаходиться на відстані R = 5 см від осі обертання, в момент часу t = 2 с. (0,8 м/с2)

    9. Тіло обертається навколо нерухомої осі так, що кут його повороту змінюється в залежності від часу t за законом φ = Вt – Ct2, де В = 2,4 рад/с, С = 0,3 рад/с2. Визначити момент часу t3, в який тіло зупиняється, та число обертів N тіла до зупинки. (4 с; 0,764 оберта)

    10. Тверде тіло обертається навколо нерухомої осі за законом φ = Вt – Dt3, де В = 6,0 рад/с, D = 2,0 рад/с3. Визначити середні значення кутової швидкості <> і кутового прискорення <> за проміжок часу від t = 0 до зупинки. Знайти кутове прискорення в момент зупинки тіла. (4 рад/с; 6 рад/с2; 12 рад/с2)

    11. Кутова швидкість тіла змінюється згідно з рівнянням = A + Bt + Ct2, де A = 3 рад/с, B = 2 рад/с2, С = 0,6 рад/с3. На який кут повернеться тіло за проміжок часу від t1 = 0 c до t2 = 10 c. Знайти середню кутову швидкість <> за цей проміжок часу. (330 рад; 33 рад/с)

    12. Тверде тіло починає обертатися навколо нерухомої осі з кутовим прискоренням = Аt, де А = 0,5 рад/с3. Через який час t після початку обертання вектор повного прискорення α довільної точки тіла буде утворювати кут α = 450 з її вектором швидкості v ? (2 с)

    13. Тверде тіло обертається навколо нерухомої осі так, що його кутова швидкість залежить від кута повороту φ за законом = 0 – Aφ, де 0 = 0,8 рад/с, А = 0,5 с-1. В момент часу t = 0 с кут φ = 00. Визначити кут повороту φ і кутову швидкість в момент часу t = 2 с. (1,01 рад; 0,29 рад/с)

    14. При обертанні маховика його кутове прискорення змінювалося за законом = А – В, де А = 0,8 рад/с2, В = 0,2 с-1. Перед гальмуванням кутова швидкість маховика 0 = 2 рад/с. Якою буде кутова швидкість маховикачерез час t = 5 с після початку гальмування? (3,3 рад/с)



    3. Динаміка матеріальної точки
      1   2   3   4

    написать администратору сайта