Главная страница
Навигация по странице:

  • (3 кг·м

  • (1 кг·м

  • (0,007 кг·м

  • (7,1 м/с

  • (4,9 м/с

  • (4,7 кг·м

  • (1,6 м/с2; 42,64 Н; 41,04 Н)

  • (3,2 рад/с; 0,2 Дж)

  • (1,50 м/с; 0,75 м/с; 1,00 м/с)

  • (0,07 с; 0,10 с; 0,75 м/с)

  • (0,08 м; 10,4 с

  • (х = 0,046 cos (πt/4 + π/8))

  • (0,5 с

  • (510 с

    		•

    док. І. механiка кінематика матеріальної точки та поступального руху тіл. Основнi формули


    Скачать 409 Kb.
    НазваниеІ. механiка кінематика матеріальної точки та поступального руху тіл. Основнi формули
    Дата05.01.2021
    Размер409 Kb.
    Формат файлаdoc
    Имя файлаdoc1 (3).doc
    ТипДокументы
    #165996
    страница3 из 4
    1   2   3   4

    Основнi формули


    1. Момент сили вiдносно заданої(го) точки (центра) 0



    де - радiус-вектор, проведений з точки (центра) 0 до точки прикладання сили .

    1. Момент сили відносно осі z



    де F – величина сили (складової сили), яка діє в перпендикулярній до осі z площині;

    ℓz - плече сили відносно осі z.

    1. Момент iмпульсу матерiальної точки вiдносно заланої(го) точки (центра)



    1. Момент iмпульсу матерiальної точки вiдносно заданої осі z



    де ℓ - плече iмпульсу матерiальної точки відносно заданої осі z

    1. Рівняння моментів



    1. Момент інерції матерiальної точки вiдносно осi



    де r - вiдстань точки вiд осi.

    1. Момент iнерцiї тiла вiдносно заданої осi



    де - вiдстань елемента маси вiд осi обертання.

    1. Момент iнерцiї тонкого обруча вiдносно осi, яка перпендикулярна до площини обруча і проходить через його центр



    де R – радіус обруча.

    1. Момент iнерцiї диска вiдносно осi, яка перпендикулярна до площини диска і проходить через його центр



    1. Момент iнерцiї стрижня вiдносно осi, яка проходить через середину стрижня i перпендикулярна до нього



    де ℓ - довжина стрижня.

    1. Момент iнерцiї кулi вiдносно осi, що проходить через її центр



    1. Момент імпульсу тіла відносно осі z



    де - кутова швидкість обертання тіла

    1. Рівняння динаміки обертального руху тіла навколо нерухомої осі



    де z – проекція вектора кутового прискорення тіла на вісь z.

    1. Закон збереження моменту iмпульсу замкненої системи



    де (Lzi) - момент iмпульсу i-го тiла вiдносно заданого(ї) центра (осi).

    1. Робота сталого моменту сили М, що дiє на тiло, яке обертається



    де - кут повороту тiла.

    1. Миттєва потужнiсть, що розвивається під час обертання тiла



    1. Кiнетична енергiя тiла, що обертається





    1. Дано однорідний суцільний диск радіусом R = 1 м і масою m = 2 кг. Визначити момент інерції J диска відносно осі, що проходить через його край і перпендикулярна до площини диска. (3 кг·м2)

    2. Дано однорідний тонкий стрижень масою m = 3 кг і довжиною ℓ = 2 м. Обчислити момент інерцій Jс стрижня відносно осі, що проходить через середину стержня перпендикулярно до нього і момент інерції J відносно осі, що проходить через кінець стрижня. (1 кг·м2; 4 кг·м2)

    3. Дано однорідну суцільну кулю масою m = 2 кг і радіусом R = 5 см. Визначити момент інерції J кулі відносно осі, що дотична до кулі. (0,007 кг·м2)

    4. При обертанні однорідного суцільного диска масою m= 10 кг навколо осі, що проходить через його центр перпендикулярно до його площини, по дотичній до диска прикладена сила F = 20 Н, і на нього діє момент сили тертя МТ = 5 Н·м. Кутова швидкість обертання диска задається рівнянням ω = А + Вt, де А = 2 рад/с, В = 4 рад/с2. Визначити радіус R диска. (0,5 м)

    5. Маховик у формі диска масою m= 10 кг і радіусом R = 0,25 м обертається з частотою n = 40 об/с. Коли вимкнути привід, маховик, зробивши N = 200 обертів, під дією тертя зупинився. Визначити момент сили тертя МТ, що діяв на маховик. (15,7 Н)

    6. Однорідний і суцільний диск масою m= 5 кг і радіусом R = 0,2 м обертається з кутовою швидкістю ω1 = 6,1 рад/с навколо осі, що проходить через центр диска. Момент сили тертя, що діє на диск, прямо пропорційний кутовій швидкості: МТ = Вω, де В = 0,01 Н·м·с/рад. Визначити кутову швидкість ω2 диска через час t = 30 с після припинення дії зовнішнього моменту сил. Скільки обертів зробить диск протягом цього часу? (0,3 рад/с; 15,3 об)

    7. По горизонтальному столі може котитися без ковзання суцільний циліндр масою m = 1,1 кг, на який намотана нитка. До вільного кінця нитки, який перекинутий через легкий блок, підвішений вантаж такої ж маси m. Визначити прискорення вантажу α1 і силу тертя FТ між циліндром і столом. (7,1 м/с2; 0,98 Н)

    8. Вал у вигляді суцільного циліндра масою m1 = 5 кг насаджений на горизонтальну вісь. На циліндр намотаний шнур, до вільного кінця якого підвішений вантаж масою m2 = 2,5 кг. З яким прискоренням α буде опускатися вантаж? (4,9 м/с2)

    9. На маховик діаметром D = 0,4 м намотаний невагомий шнур, до вільного кінця якого прив’язаний вантаж масою m = 5 кг. Обертаючись рівноприскорено під дією сили тяжіння вантажу, маховик за час t = 4 с набув кутову швидкість ω = 8 рад/с. Визначити момент інерції J маховика. (4,7 кг·м2)

    10. Два вантажі масами m1 = 5,2 кг і m2 = 3,6 кг з’єднані невагомою ниткою, яка перекинена через нерухомий блок у вигляді однорідного суцільного диска масою m = 2 кг. Нехтуючи тертям в осі блока, визначити прискорення α, з яким будуть рухатися вантажі, і сили натягу Т1 і Т2 нитки по обидві сторони блока. (1,6 м/с2; 42,64 Н; 41,04 Н)

    11. На барабан радіусом R = 0,1 м, момент інерції якого І = 0,03 кг·м2, намотаний шнур, до кінця якого прив’язаний вантаж масою m = 2 кг. До початку обертання барабана висота вантажу над підлогою h = 2 м. Визначити кінетичну енергію Ек вантажу в момент удару об підлогу, час t, за який вантаж опуститься до підлоги і силу натягу Т шнура. Тертям знехтувати. (7,84 Дж; 1 с; 11,68 Н)

    12. Обруч та суцільний диск однакової маси котяться без проковзування з однаковою швидкістю. Кінетична енергія диска Екд = 12 Дж. Визначити кінетичну енергію Екоб обруча. (16 Дж)

    13. Обруч, суцільний диск і куля скочуються без проковзування з похилої площини з кутом нахилу α = 300. Початкові швидкості тіл дорівнюють нулю. Визначити лінійні прискорення центрів мас цих тіл. (αоб =2,45 м/с2; αд = 3,27 м/с2; αк= 3,50 м/с2)

    14. Однорідний тонкий стрижень довжиною ℓ = 1,1 м, який закріплений так, що він може обертатись навколо горизонтальної осі, яка проходить перпендикулярно до стрижня через один з його кінців, відводять від вертикального положення на кут α = 600 і потім відпускають. Визначити швидкість v нижнього кінця стрижня в момент проходження ним положення рівноваги. (4 м/с)

    15. Олівець довжиною ℓ = 0,13 м, який поставлений вертикально, падає на стіл. Яку кутову ω та лінійну v швидкості будуть мати в кінці падіння середина та верхній кінець олівця? (ω1= ω2 = 15 рад/с; v1 = 0,98 м/с; v2 = 1,95 м/с)

    16. Залізна куля радіусом R = 0,1 м обертається з частотою n = 3 об/с навколо осі, що проходить через її центр. Яку роботу А необхідно виконати, щоб збільшити кутову швидкість кулі вдвічі? Густина заліза ρ = 78700 кг/м3. (70,17 Дж)

    17. На платформі у вигляді диска сидить людина і тримає у витягнутих руках гирі масою по m = 5 кг кожна. Відстань від кожної гирі до осі обертання лави ℓ1 = 0,6 м. Платформа обертається з частотою n1 = 2 об/с відносно осі, що проходить через центр мас людини і платформи. Сумарний момент інерції людини і платформи відносно осі обертання J0 = 2,1 кг м2. Людина стискає руки так, що відстань від кожної гирі до осі стане ℓ2 = 0,3 м. Якою буде тепер частота n2 обертання платформи і яку роботу А виконає людина? (3,8 об/с; 404,6 Дж)

    18. Платформа у вигляді диска радіусом R = 2,0 м і масою m1 = 160 кг обертається навколо вертикальної осі, що проходить через її центр, з кутовою швидкістю ω1 = 1,5 рад/с. У центрі платформи стоїть людина масою m2 = 70 кг. Людина переходить на край платформи. Якою буде лінійна швидкість людини v відносно підлоги? (1,6 м/с)

    19. Два гумових диски з жорсткими поверхнями обертаються навколо осей, що лежать на одній вертикалі, причому площини дисків паралельні. Перший диск має момент інерції J1 = 2 кг м2 і кутову швидкість ω1 = 3 рад/с, другий - J2 = 0,5 кг м2 і ω 2 = 4 рад/с. Верхній диск падає на нижній і з’єднується з ним. Визначити кутову швидкість ω дисків і зміну їх кінетичної енергії ΔЕк. (3,2 рад/с; 0,2 Дж)


    6. Механiчнi коливання.
    Основнi формули


    1. Диференціальне рiвняння гармонiчних коливань i його розв'язок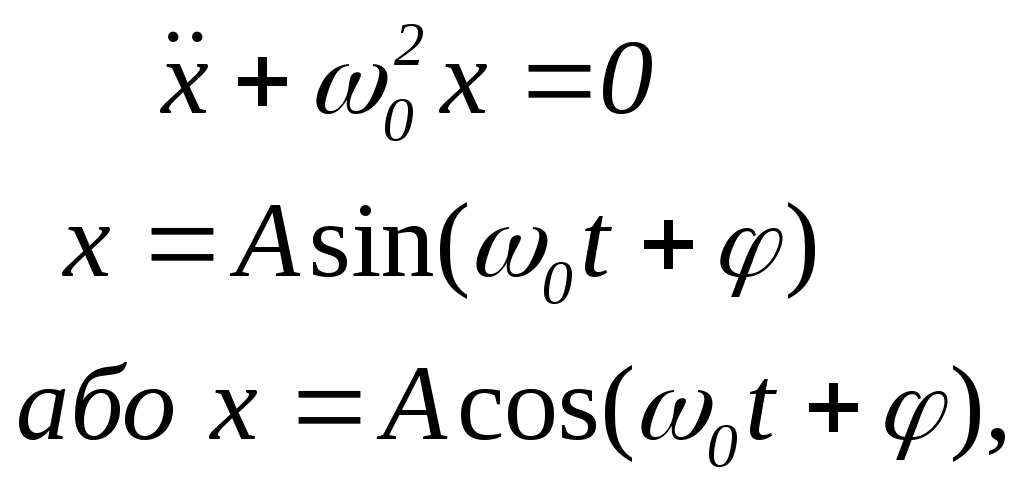



    де; А - амплiтуда коливань;

    о- колова (циклiчна) частота власних коливань;

    о - початкова фаза коливань.

    1. Рiвняння загасаючих коливань при врахуванні сили опору



    де - коефiцiєнт загасання ( );

     - частота загасаючих коливань ( ).

    1. Логарифмiчний декремент загасання



    1. Диференційне рiвняння вимушених коливань i його розв'язок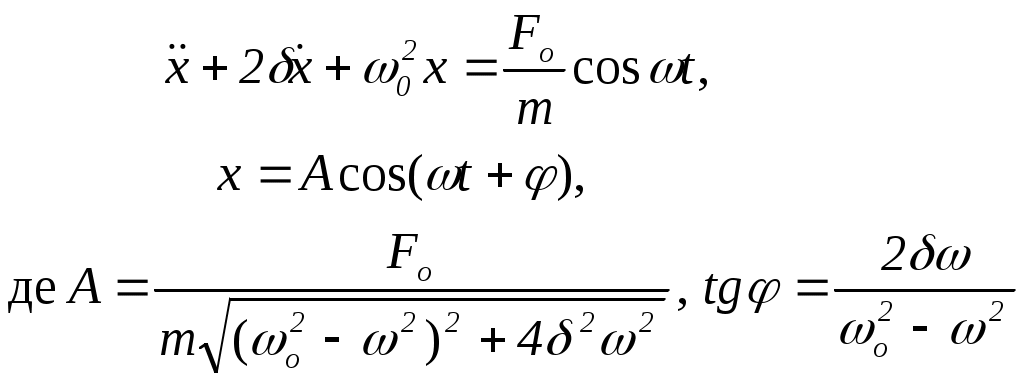



    1. Перiод коливань пружинного маятника



    де m - маса тiла; k - жорсткiсть пружини.

    1. Перiод коливань математичного маятника



    де l - довжина маятника; g - прискорення вiльного падiння.

    1. Період коливань фізичного маятника



    де J – момент інерції маятника відносно точки її підвісу;

    ℓ - відстань між точкою підвісу і центром мас маятника

    1. Довжина хвилі



    1. Рівняння плоскої хвилі, яка поширюється вздовж осі x



    де k – хвильове число ( ).

    1. Густина потоку енергії, що переноситься хвилею (вектор Умова)



    де w – об’ємна густина енергії хвилі.



    1. Матеріальна точка, відносно положення рівноваги виконує гармонічні коливання вздовж деякої прямої з періодом Т = 0,4 с і амплітудою А = 0,1 м. Визначити середню швидкість <v> точки за час, протягом якого вона проходить шлях, що дорівнює першій половині амплітуди, другій половині і цілій амплітуді. (1,50 м/с; 0,75 м/с; 1,00 м/с)

    2. Матеріальна точка здійснює гармонічні коливання вздовж горизонтальної прямої з періодом Т = 0,4 с і амплітудою А = 0,1 м, починаючи рух з крайнього положення. За який час, рахуючи від початку руху, точка пройде відстані S1 = A/2 і S2 = А? Визначити середню швидкість <v> на шляху S1. (0,07 с; 0,10 с; 0,75 м/с)

    3. Точка виконує гармонічні коливання за законом , де А = 0,04 м, Т = 4,35 с, φ = 0. Визначити швидкість v точки в момент часу, коли вона перебуває на віддалі x = 0,02 м від положення рівноваги. (0,05 м/с)

    4. На тіло масою m = 2 кг діє сила, яка змінюється за законом F = F0 cos ωt, де F0 = 4,0 Н, ω = 1,57 с-1. У момент часу t = 0 зміщення тіла від положення рівноваги x = 0 і швидкість v = 0. Показати, що такий рух є коливальним. Визначити період коливань Т, максимальне значення зміщення xmax і максимальне значення швидкості vmax. (4 с; 0,81 м; 1,3 м/с)

    5. Матеріальна точка одночасно бере участь у двох коливаннях одного напрямку, які описуються рівняннями x1 = A cos ωt і x2 = A cos 2ωt, де А = 0,25 м, ω = 4 с-1. Визначити максимальну швидкість vmax точки. (2,73 м/с)

    6. Матеріальна точка здійснює гармонічні коливання за законом x = A sin (ωt+φ) вздовж осіox. Через час t1 = 0,05 с від початку руху зміщення точки від положення рівноваги x1 = 0,05 м, швидкість v1 = 0,62 м/с, прискорення α1 = -5,40 м/с2. Визначити амплітуду А, циклічну частоту ω і початкову фазу коливань φ. Чому дорівнює зміщення x0, швидкість v0 і прискорення α0 в початковий момент часу t = 0 ? (0,08 м; 10,4 с-1; π/18; 0,01 м; 0,80 м/с; 1,47 м/с2)

    7. Легкий стрижень може вільно обертатися навколо горизонтальної осі. На відстані S = 3 см від осі на ньому закріплено невелику кульку і потім на відстані d = 2 см одна від одної – ще дві такі самі кульки. Визначити період коливань цієї системи. (0,47 с)

    8. На гладенькому горизонтальному столі лежить тіло масою m1 = 10 кг, яке закріплено до стінки пружиною жорсткістю k = 250 Н/м. У тіло попадає куля масою m2 = 0,01 кг і швидкістю v2 = 500 м/с у напрямку осі пружини і застрягає в тілі. Визначити період Т коливань тіла та амплітуду А. (1,26 с; 0,1 м)

    9. Матеріальна точка масою m = 0,1 кг виконує гармонічні коливання за законом x = 4 sin (2t + π/4) см. Визначити максимальну силу Fmax, що діє на точку і повну енергію Е точки, що коливається. (16 мН; 320 мкДж)

    10. Амплітуда гармонічних коливань матеріальної точки А = 0,12 м, повна енергія коливань Е = 6 мкДж. При зміщенні х від положення рівноваги на точку, що коливається, діє сила F = 50 мкН. Визначити величину зміщення х. (0,06 м)

    11. Матеріальна точка бере участь одночасно у двох косинусоїдальних коливаннях одного напряму з однаковими амплітудами А = 0,025 м і однаковими періодами Т = 8 с. Різниця фаз між цими коливаннями φ2 – φ1 = π/4. Початкова фаза одного з цих коливань дорівнює нулю. Написати рівняння результуючого руху. (х = 0,046 cos (πt/4 + π/8))

    12. Матеріальна точка бере участь одночасно у двох взаємно перпендикулярних коливаннях, що описуються рівняннями x = sin ωt і y = 2 sin 2ωt. Визначити рівняння траєкторії точки та намалювати траєкторію. (16x4 - 16x2 + y2 = 0)

    13. Матеріальна точка одночасно бере участь у двох взаємно перпендикулярних коливаннях, що описуються рівняннями x = 2 cos πt/2 і y = -cos πt. Визначити рівняння траєкторії точки та намалювати траєкторію. ( )

    14. Амплітуда згасаючих коливань математичного маятника за час t1 = 2 хв. зменшилась в n1 = 3 рази. Визначити у скільки разів n2 зменшиться амплітуда за час t2 = 8 хв. (81 раз)

    15. Математичний маятник довжиною ℓ = 0,16 м виконує коливання у середовищі, в якому коефіцієнт згасання δ = 0,4 с-1.За певний час амплітуда коливань маятника зменшилася в n = 5 разів. Визначити цей час і число коливань N, які виконав маятник. (4,02 с; 5,0)

    16. Тіло масою m = 0,76 кг, яке підвішене до пружини жорсткістю k = 30 Н/м, виконує в деякому середовищі пружні коливання. Логарифмічний декремент коливань æ = 0,01. Через який проміжок часу Δt енергія коливань тіла зменшиться у n = 7,4 рази. (100 с)

    17. Матеріальна точка виконує у вакуумі коливання з циклічною частотою ω0 = 3,0 с-1 і амплітудою А0 = 0,16 м. У в’язкому середовищі циклічна частота її коливань стала рівною ω = 2,9 с-1. Визначити амплітуду швидкості vmax точки у середовищі через час t = 2 с після початку руху. (0,10 м/с)

    18. Вантаж масою m = 1 кг, який підвішений на пружині жорсткістю k = 100 Н/м, здійснює коливання у в’язкому середовищі з коефіцієнтом опору r = 1 кг/с. На верхній кінець пружини діє вимушуюча сила, що змінюється за законом F = F0 cos ωt, де F0 = 0,2 Н. Визначити для даної коливної системи коефіцієнт згасання δ і резонансну амплітуду Арез. (0,5 с-1; 0,02 м)

    19. Амплітуди вимушених гармонічних коливань дорівнюють одна одній при циклічних частотах ω1 = 400 с-1 і ω2 = 600 с-1. Визначити частоту ωр, при якій амплітуда цих вимушених коливань є максимальна. (510 с-1)

    20. Тіло масою m = 0,05 кг здійснює згасаючі коливання з початковою амплітудою А0 = 0,12 м, початковою фазою φ0 = 0 і коефіцієнтом згасання δ = 2,0 с-1. На це тіло почала діяти зовнішня періодична сила F, під дією якої встановилися вимушені коливання. Рівняння вимушених коливань має вигляд х = 0,10 cos(10πt – 3π/4) м. Знайти рівняння згасаючих коливань тіла і рівняння зовнішньої періодичної сили. ( )

    21. Стрілка чутливого приладу коливається біля положення рівноваги. Її послідовні крайні положення такі: n1 = 26,4; n2 = 10,7, n3 = 20,5. Знайти поділку, яка відповідає рівноважному положенню стрілки, якщо її декремент згасання є сталим у часі. (16,7)

    1   2   3   4

    написать администратору сайта