Економико математичне моделювання в бизнеси заочка Галушко. Контрольна робота з предмету Економікоматематичне моделювання в бізнесі
 Скачать 0.55 Mb.
|
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ХМЕЛЬНИЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ФАКУЛЬТЕТ УПРАВЛІННЯ, АДМІНІСТРУВАННЯ ТА ТУРИЗМУ Контрольна робота З предмету «Економіко-математичне моделювання в бізнесі» Варіант №14 Виконав студент групи МНз-17-1 Галушко Т.С. Перевірив к.е.н., доц. Остапчук О.В. Хмельницький 2022 ВАРІАНТ 10 ЗАДАЧА 1 За допомогою графічного методу визначити оптимальний план задачі лінійного програмування, математична модель якої наведена нижче 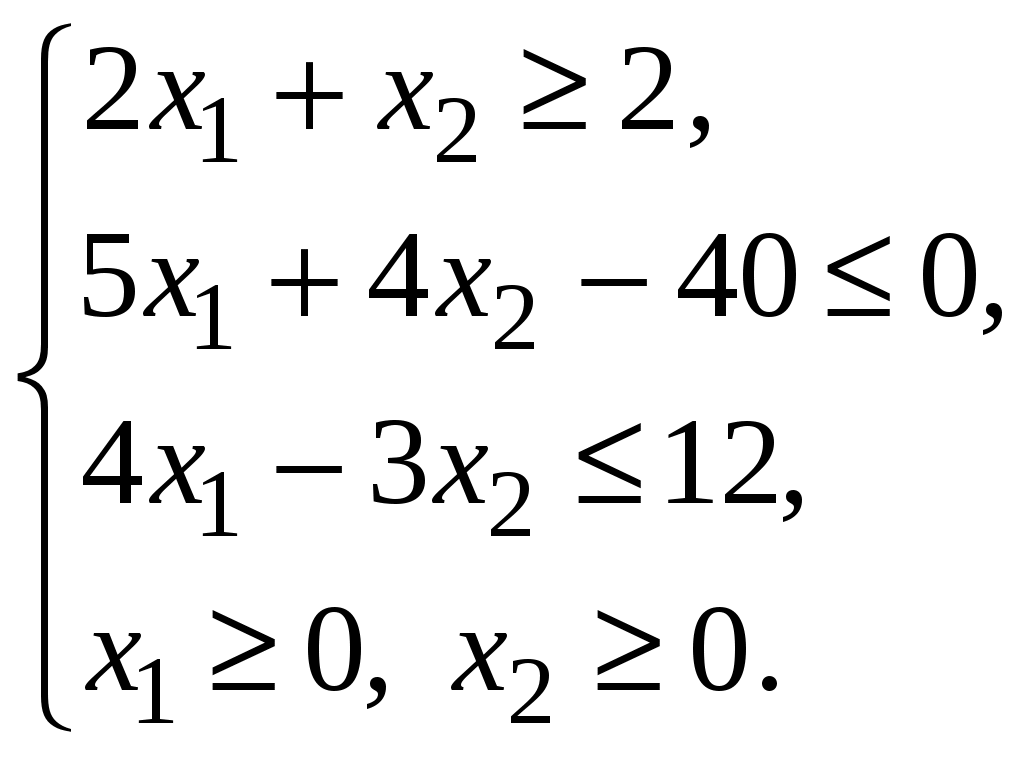  Розв’язання. Побудуємо прямі: 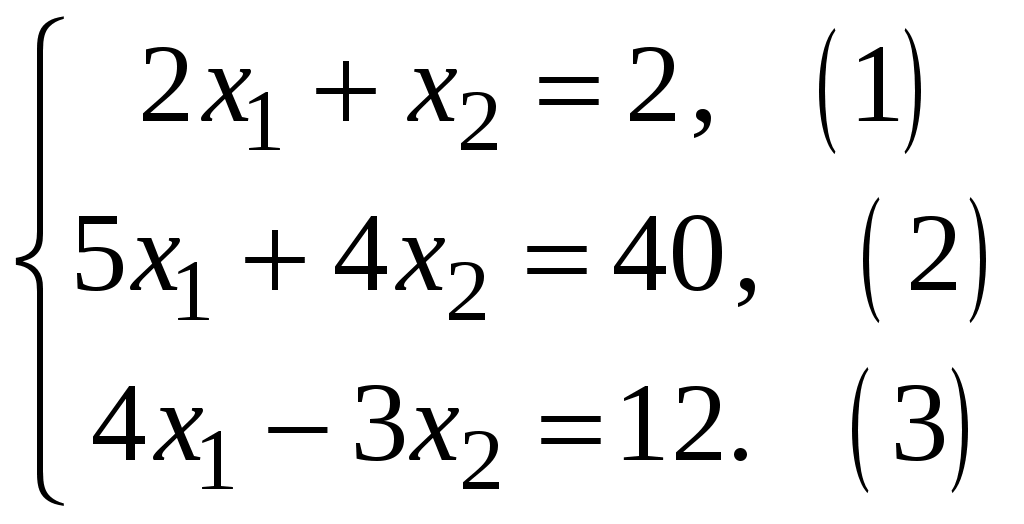 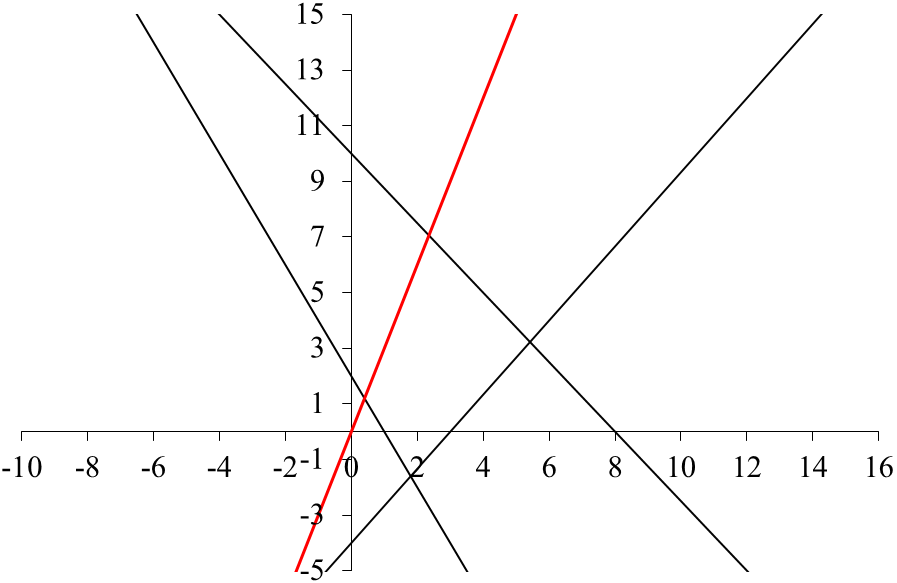 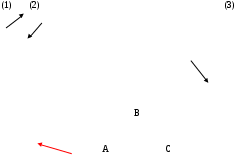 ABС – трикутник можливих розв’язків. Мінімум в точці С. Знайдемо її координати: 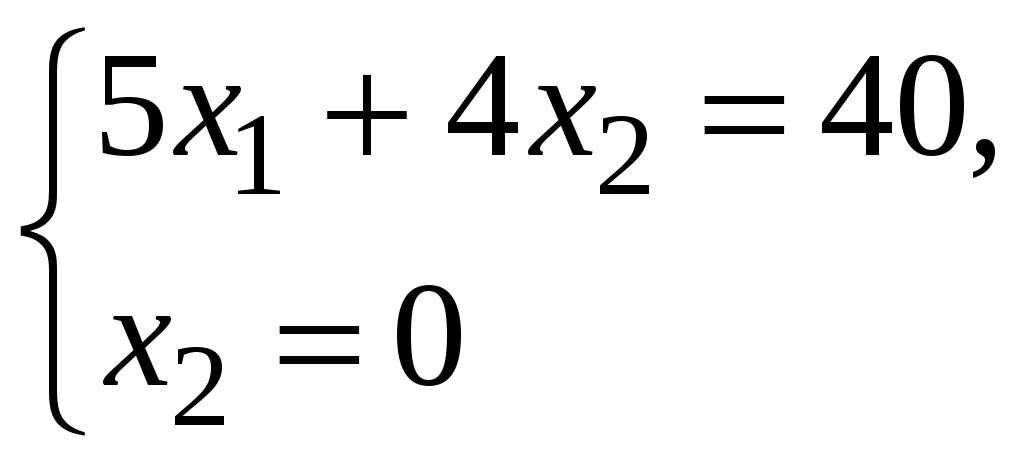 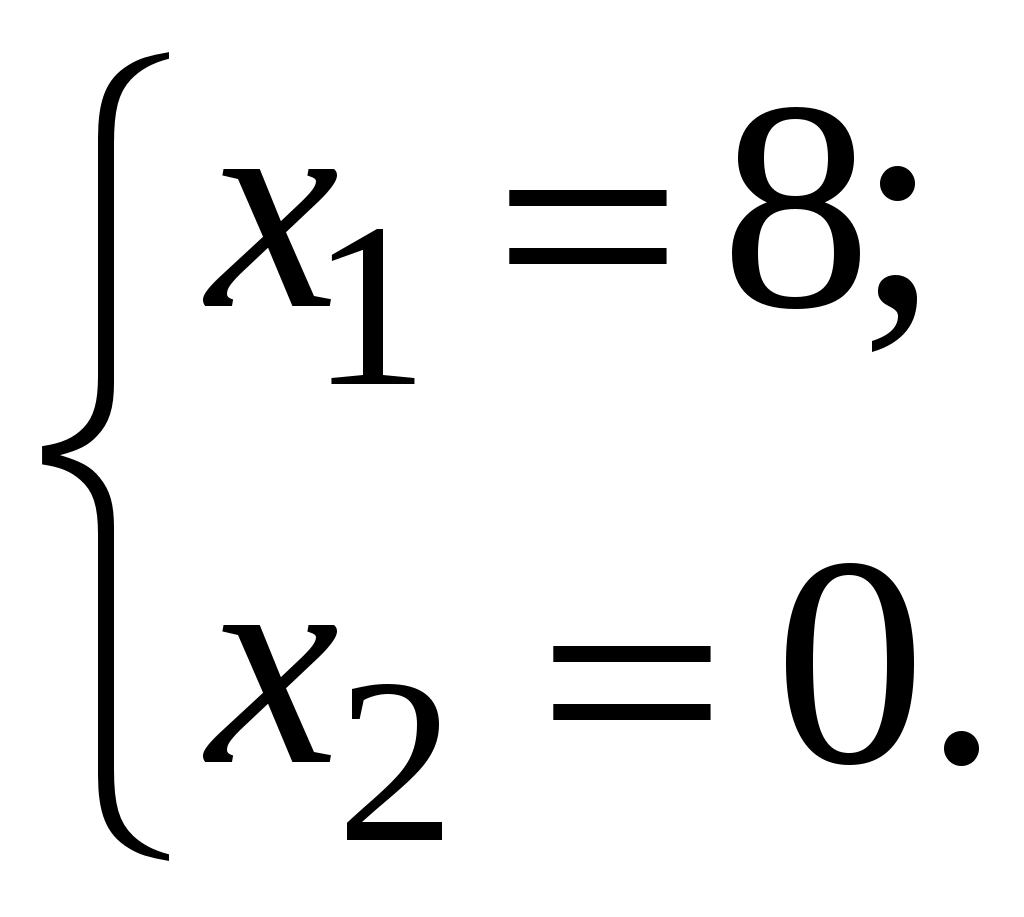   і  .ЗАДАЧА 2 Цех має можливість виробляти продукцію двох видів А та В. При цьому він використовує три види сировини, запаси якої обмежені й складають відповідно  ,  та  умовних одиниць. Прибуток від реалізації одиниці продукції кожного виду становить  та  умовних одиниць. Кількість сировини, що витрачається на виготовлення одиниці продукції А, визначається матрицею  , а продукції В − матрицею  . За допомогою симплексного методу визначити оптимальний план виробництва, за яким цех матиме максимальний прибуток.Розв’язання. Побудуємо математичну модель задачі. Позначимо через 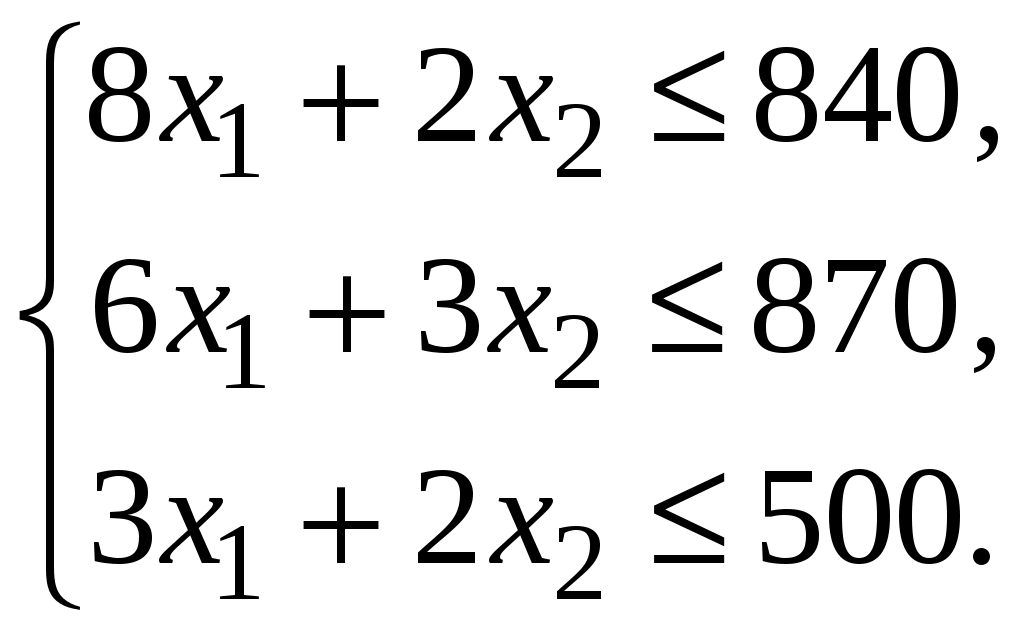 кількість одиниць виробу А, через  – виробу В, тоді прибуток від реалізації готової продукції є функцією двох змінних:  . Оскільки кількість сировини, що витрачається на виготовлення продукції, не може перевищувати її запасів, то обмеження за кожним видом сировини можна записати в вигляді нерівностей, які утворюють основну систему обмежень: Крім того, кількість продукції не може бути від’ємною, тобто існує обмеження на знак: 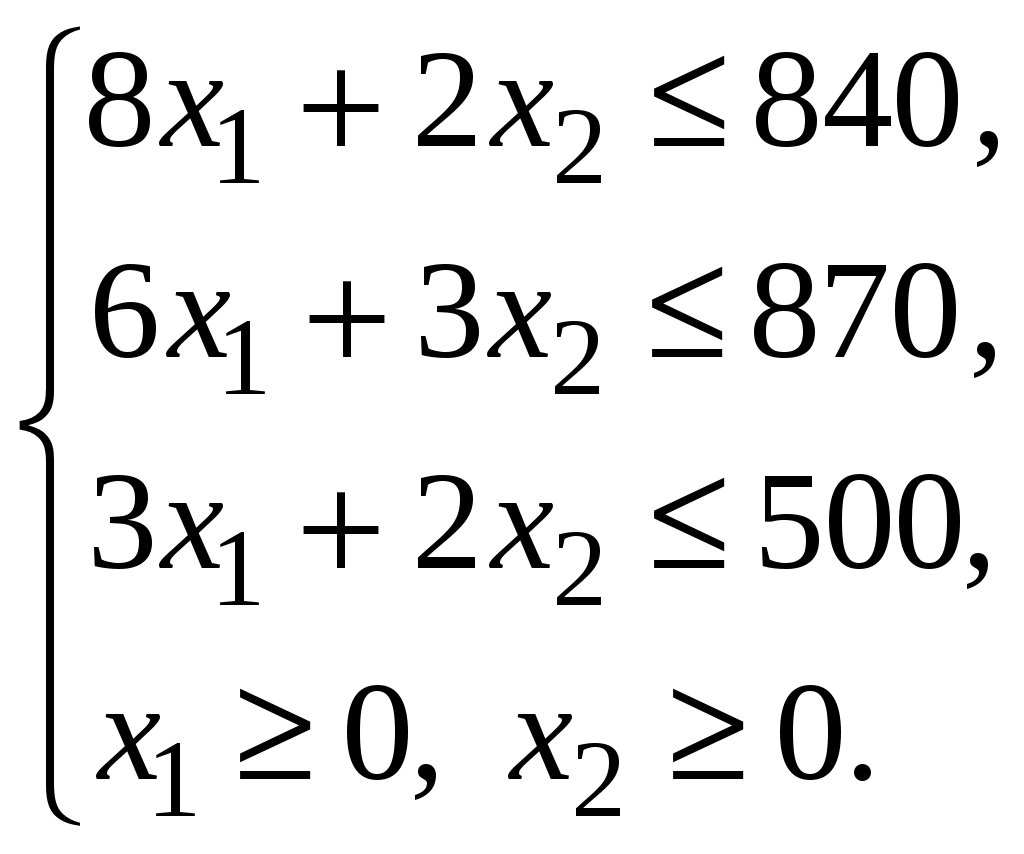 ,  . Отже, математична модель задачі має вигляд: , Запишемо задачу в канонічній формі 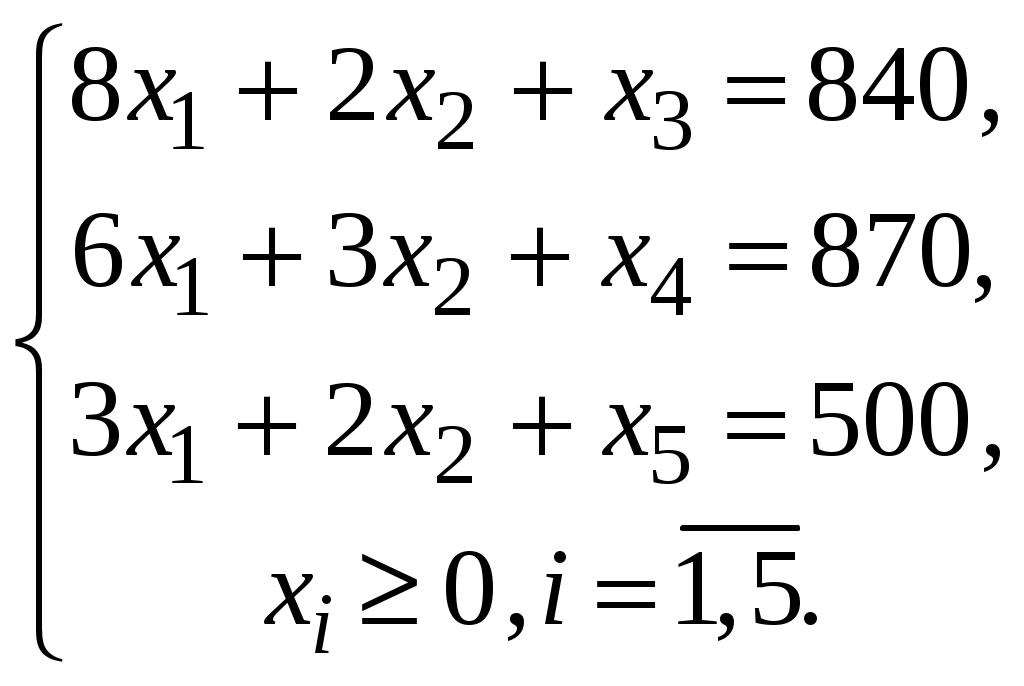  Складемо симплекс-таблицю і перевіримо план на оптимальність:
 В строчці  є від’ємні елементи, тому план неоптимальний. Вибираємо направляючий елемент, виконуємо необхідні перетворення, складаємо новий опорний план і перевіряємо його на оптимальність.
 В строчці є від’ємні елементи, тому план неоптимальний. Вибираємо направляючий елемент, виконуємо необхідні перетворення, складаємо новий опорний план і перевіряємо його на оптимальність.
В строчці немає від’ємних елементів, тому план оптимальний. .Найбільший прибуток, який дорівнює 1250 умовним одиницям, цех отримає, якщо з наявної сировини випускатиме 0 одиниць продукції А та 250 одиниць продукції В. При цьому сировина третього виду буде витрачена, а залишок сировини першого і другого виду становитиме відповідно 340 і 36,67 одиниць. ЗАДАЧА 3 Для матричної гри «Покупець-продавець», що задана платіжною матрицею П, обчислити нижню та верхню вартості гри, визначити ціну гри та оптимальні стратегії кожного із гравців, застосувавши графічний метод: 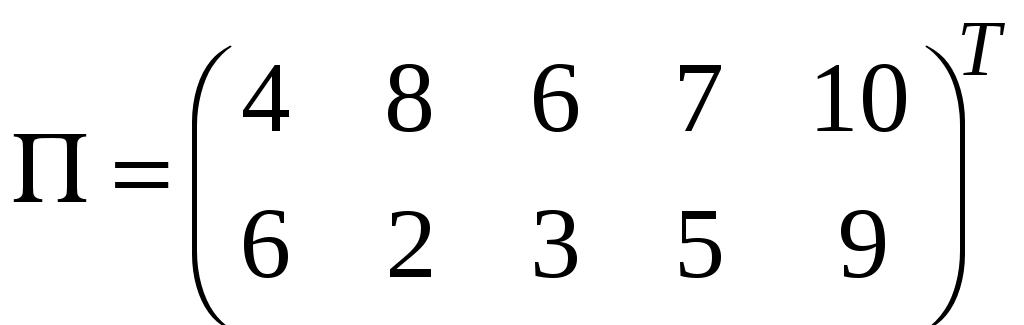 .Розв’язання. Відповідно до платіжної матриці гравець А має дві стратегії: А1 та А2, в той час гравець В має п’ять стратегій: В1, В2, В3, В4 та В5: 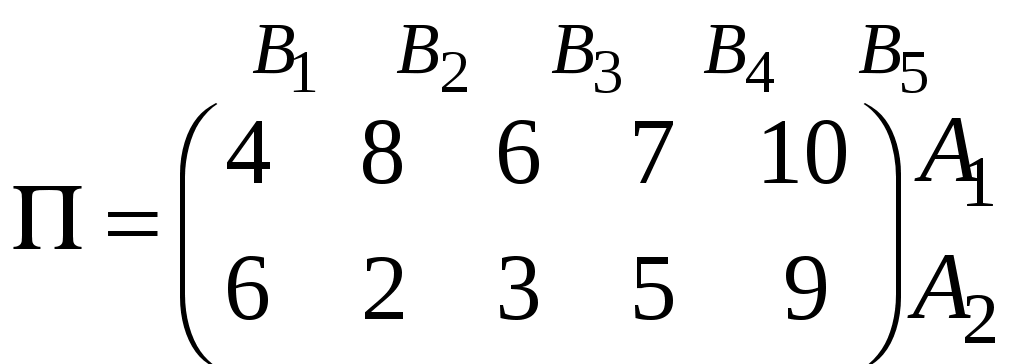 .Перевіримо, чи має гра сідлову точку. Для цього визначимо нижню ціну гри  , тобто порівняємо найменші значення виграшів за кожним із рядків платіжної матриці (стратегії гравця А) та виберемо серед них найбільше:  .Визначимо верхню ціну гри  , тобто порівняємо найбільші значення програшів за кожним стовпцем платіжної матриці (стратегії гравця В) та виберемо серед них найменше:  .Оскільки  , то гра не має сідлової точки, отже, вона має розв’язок у мішаних стратегіях, при цьому ціна гри  задовольняє умові:  . Розв’яжемо задачу за допомогою графічного методу. Це можна зробити, оскільки гравець А має тільки дві стратегії.На координатній площині вздовж осі абсцис відкладемо відрізок одиничної довжини. Перпендикулярно йому проводимо осі 0А1 та 1А2, на яких відкладаємо виграші гравця А, що відповідають стратегіям А1 та А2 за умов, що гравець В дотримується однієї із своїх стратегій (рис.). 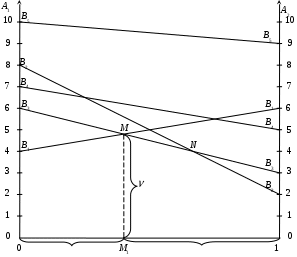 Ламана лінія В1MNB2 є нижньою границею можливого виграшу гравця А. На цій границі знаходимо точку з максимальною ординатою. Видно, що це точка М, що утворена перетином ліній В1В1 та В3В3, які відповідають стратегіям В1 та В3 гравця В. Ордината точки М відповідає ціні гри, а відрізки 0М1 та М11, на які проекція точки М поділяє одиничний відрізок осі абсцис, визначають імовірності  та  , з якими гравець А буде дотримуватися відповідно стратегій А2 та А1.Отже, точка М знаходиться на перетині ліній В1В1 та В3В3. Тоді в активних стратегіях платіжна матриця має вигляд: 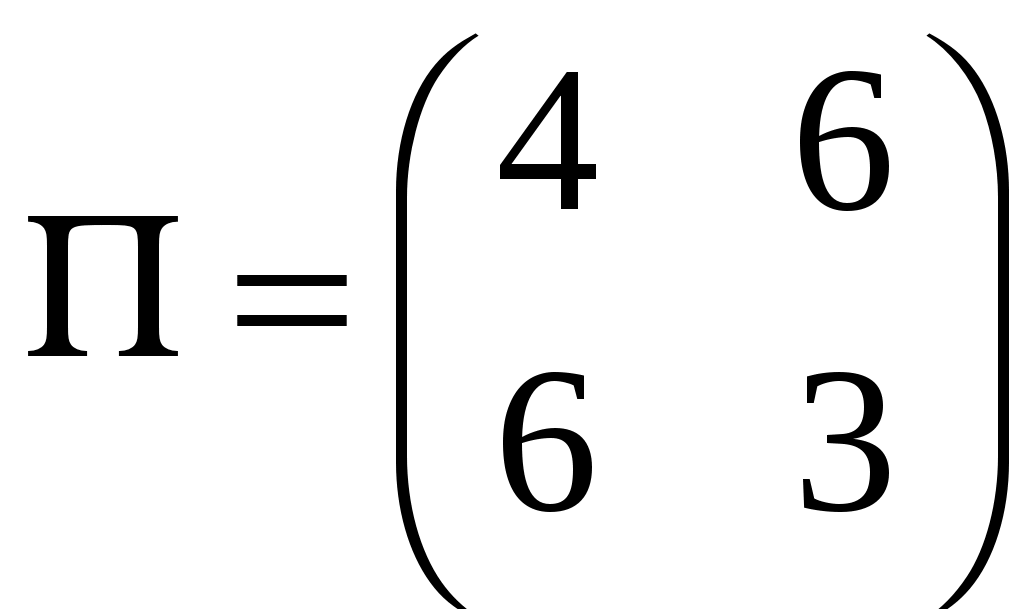 .За цією матрицею оптимальну стратегію гравця А визначає вектор 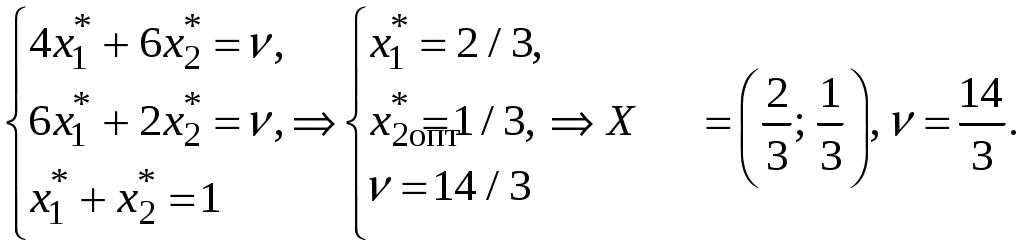 , а гравця В – вектор  . Для розв’язання задачі складемо систему рівнянь відносно компонентів вектора  та ціни гри. В перших двох рівняннях цієї системи коефіцієнтами при невідомих  та  є елементи платіжної матриці активних стратегій, що стоять у її стовпцях (тобто фіксованими є стратегії гравця В). Оскільки використання гравцем А або своєї стратегії А1, або стратегії А2 утворює повну групу подій, то сума ймовірностей цих подій дорівнює одиниці. Це й буде третім рівнянням системи. Отже, маємо: Для обчислення компонентів 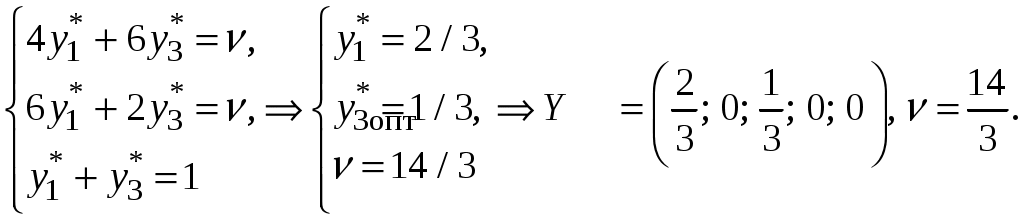 та  вектора  , які визначають імовірність вибору певної стратегії гравцем В., запишемо систему рівнянь, коефіцієнтами яких є елементи рядків платіжної матриці активних стратегій (тобто фіксованими є стратегії гравця А): Видно, що значення ціни гри, які обчислювалися відповідно до оптимальних стратегій обох гравців, однакові й збігаються з даними, що були отримані при аналізі графічного розв’язку. ЗАДАЧА 4 За емпіричними даними щодо продуктивності праці (Y), фондозабезпеченності (X1) (тис. грн.) та стажем роботи в роках (X2) побудувати економетричну модель у стандартизованих і натуральних змінних; визначити основні числові характеристики; перевірити значущість регресії за критерієм Фішера; встановити доцільність присутності факторів у рівнянні регресії за допомогою часткових F-критеріїв Фішера.
Розв’язання. Якщо розглядати сукупність X1, X2 та Y як тривимірну випадкову величину, то вона має дев’ять основних числових характеристик, а саме: вибіркові середні кожного з 3-х компонентів, їх середні квадратичні відхилення та парні коефіцієнти кореляції між усіма компонентами випадкової величини. Наведемо формули для обчислення основних числових характеристик емпіричного розподілу. Так, вибіркова середня за незгрупованими даними визначається із співвідношення: 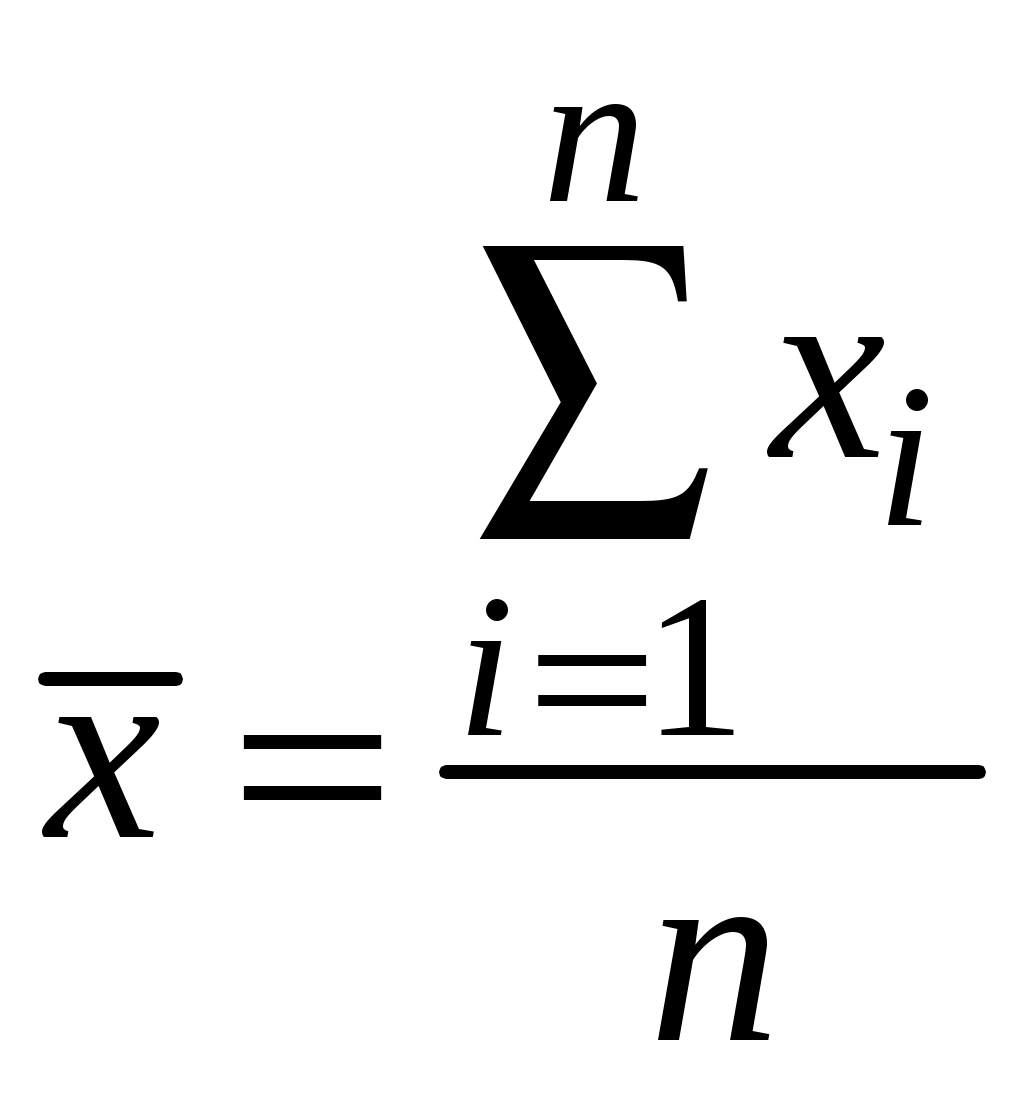 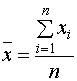 ,де  − значення  -ї варіанти ( ); − обсяг вибіркової сукупності (кількість варіант).Вибіркова середня є незсунутою оцінкою середньої генеральної сукупності. Для обчислення дисперсії будь-якої з випадкових величин за незгрупованими даними зручно застосовувати формулу: 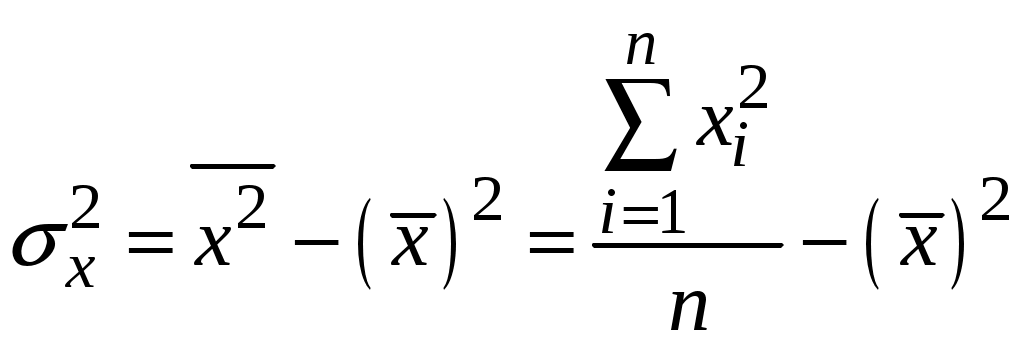 .Звідси отримуємо середнє квадратичне відхилення:  .Оскільки при обчисленні дисперсії як суми квадратів відхилень випадкової величини від її вибіркової середньої отримаємо зсунуту оцінку дисперсії генеральної сукупності, то необхідно ввести поправку на зсув. Відповідно матимемо виправлену дисперсію:  .Звідси маємо виправлене середнє квадратичне відхилення:  .Вибіркова середня та середнє квадратичне відхилення характеризують кожну з компонентів тривимірної випадкової величини окремо. Як характеристика кореляційного зв’язку між окремими компонентами цієї випадкової величини застосовуються парні коефіцієнти кореляції. Наприклад, парний коефіцієнт кореляції між компонентами Х та Y обчислюється за формулою: 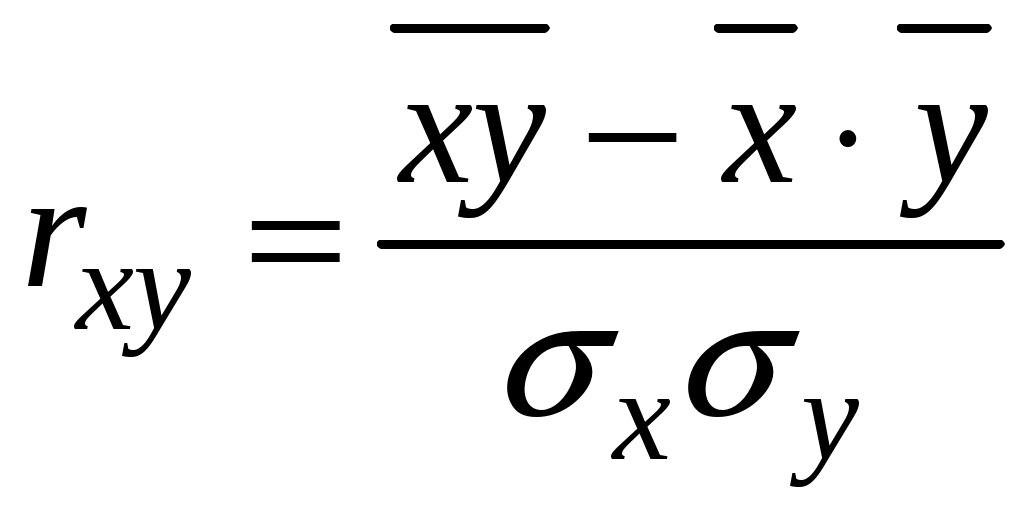 ,де  − середнє добутку випадкових величин.Допоміжні обчислення для визначення основних числових характеристик виконуємо в таблиці.
Обчислимо основні числові характеристики емпіричного розподілу за формулами, що надані вище, і узагальнимо результати в таблиці:
Побудуємо економетричну модель задачі в натуральних та стандартизованих змінних. Стандартизована змінна, що відповідає натуральній змінній Xj (в даному випадку це змінні X1, X2 та Y), задається співвідношенням: 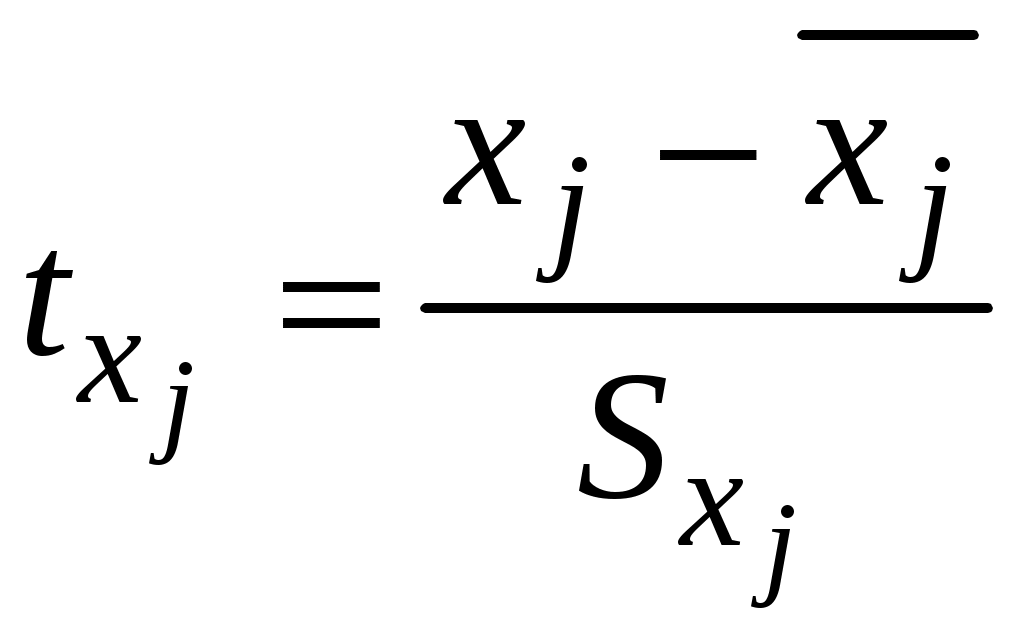 .У стандартизованих змінних економетрична модель має вигляд:  ,де  та  − статистичні оцінки параметрів моделі ( – коефіцієнти).Оцінювання параметрів множинної регресії здійснюється за методом найменших квадратів (МНК). Значення 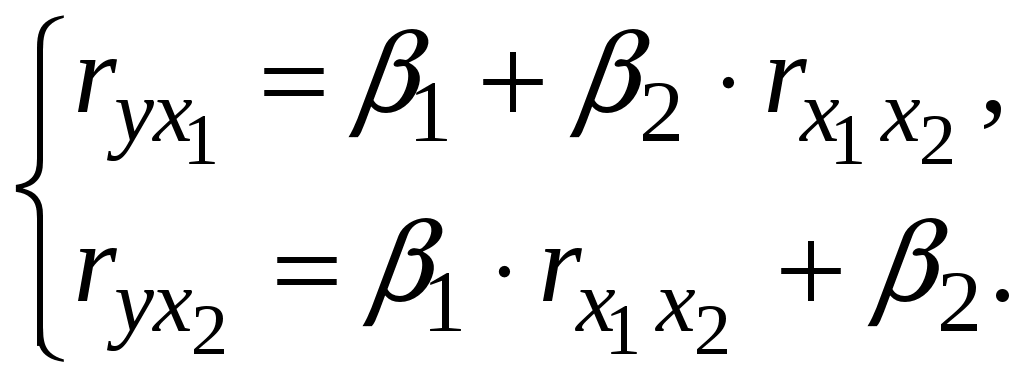-коефіцієнтів знаходять як розв’язок системи рівнянь: Отже, маємо: 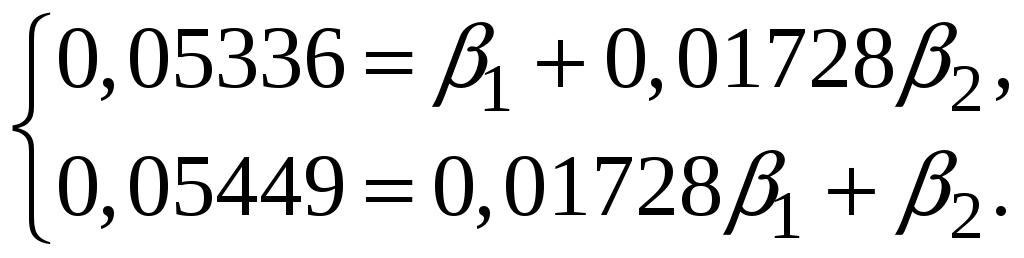 Звідси знаходимо, що  та  . Тепер записуємо економетричну модель у стандартизованих змінних: .Оскільки  , то можна стверджувати, що витрати X2, які пов’язані зі стажем роботи, найбільш сильно впливають на продуктивність праці Y.Запишемо загальний вид економетричної моделі в натуральних змінних:  ,де  ,  та  − параметри моделі.При побудові моделі в натуральних змінних коефіцієнти при невідомих визначаються співвідношеннями: 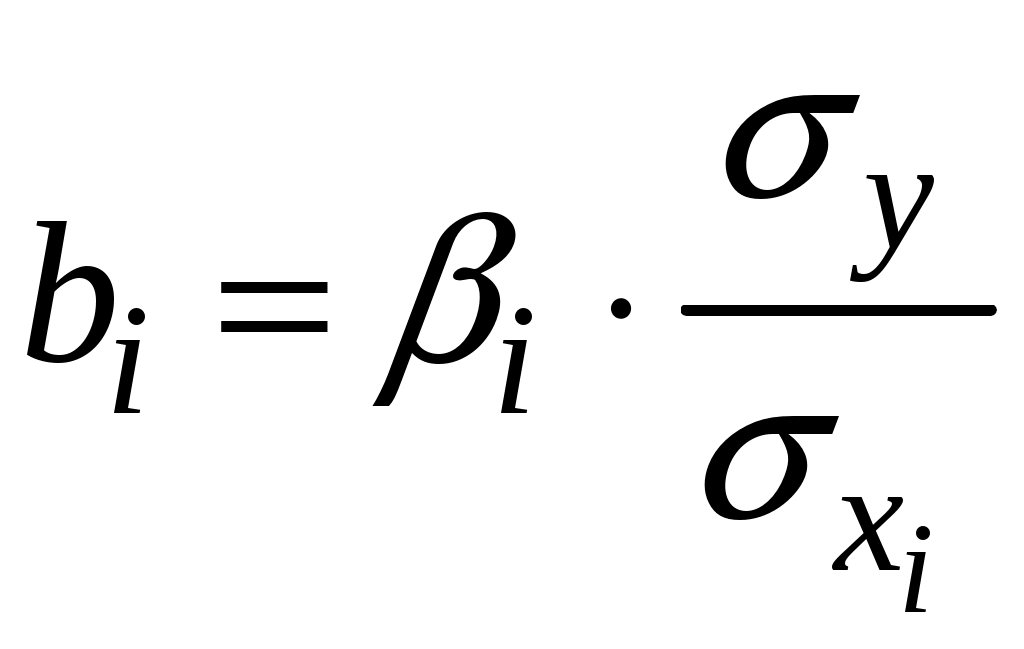 ,  ,а вільний член рівняння обчислюється з умови, що координати центру вибіркової сукупності задовольняють рівнянню регресії:  .Отримуємо: 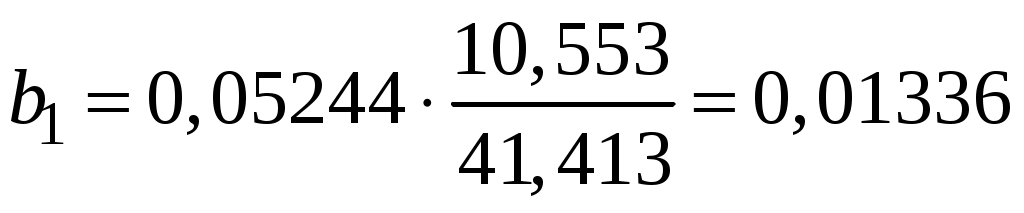 , 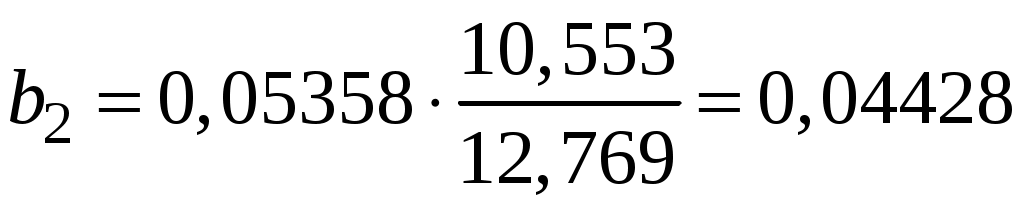 .Отже, у натуральних змінних економетрична модель має вигляд:  .Обчислимо часткові коефіцієнти продуктивності праці, яка є функцією двох змінних: фондозабезпеченності X1 та стажем роботи X2. За формулою: 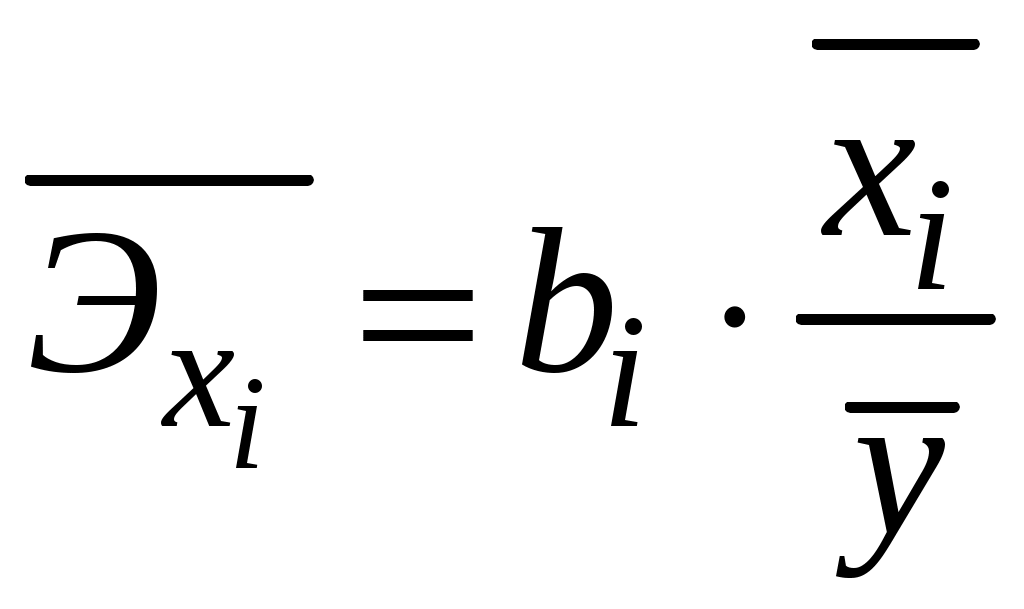 , ,відповідно отримуємо: 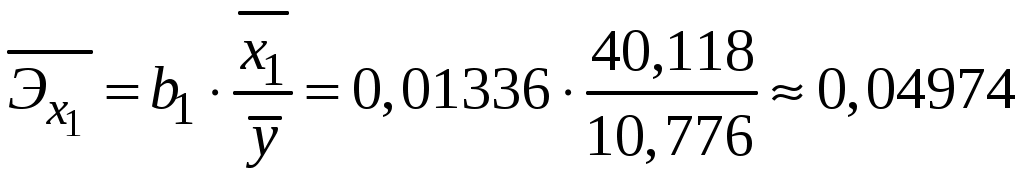 , 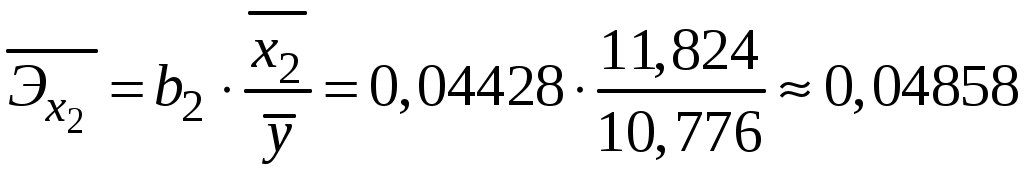.Звідси випливає, що при збільшенні фондозабезпеченності (X1) на 1% середнє значення продуктивності праці (Y) збільшиться на 0,04974%; та зі збільшенням стажу роботи (X2) на 1% середнє значення продуктивності праці (Y) збільшиться на 0,04858%. Тепер обчислимо основні характеристики економетричної моделі. Частинні коефіцієнти кореляції, що вимірюють вплив окремого фактора Xi ( 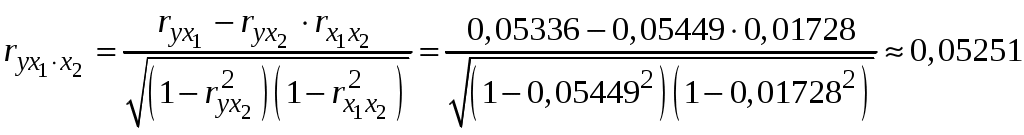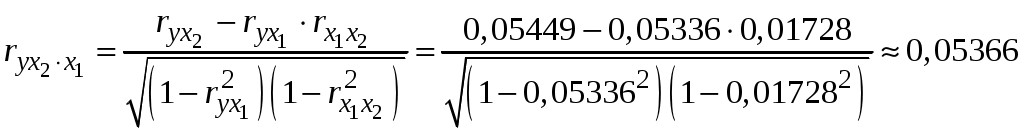) на ознаку Y при незмінному рівні іншого фактора, обчислюються за формулами: , .Визначимо частинний коефіцієнт кореляції, що вимірює вплив фактора X2 на X1 при незмінному рівні ознаки Y: 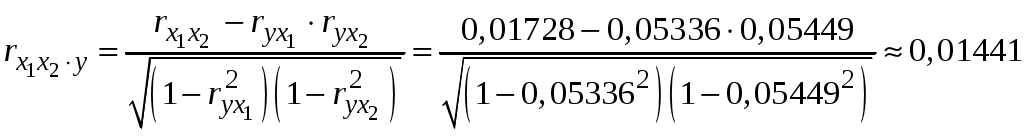 .Оскільки зв’язок між факторами практично відсутній (  є близьким до нуля), то частинні коефіцієнти кореляції практично не відрізняються від коефіцієнтів парної кореляції.Перевіримо значущість частинних коефіцієнтів кореляції за критерієм Стьюдента. Для цього визначимо дисперсію частинних коефіцієнтів кореляції за формулою: 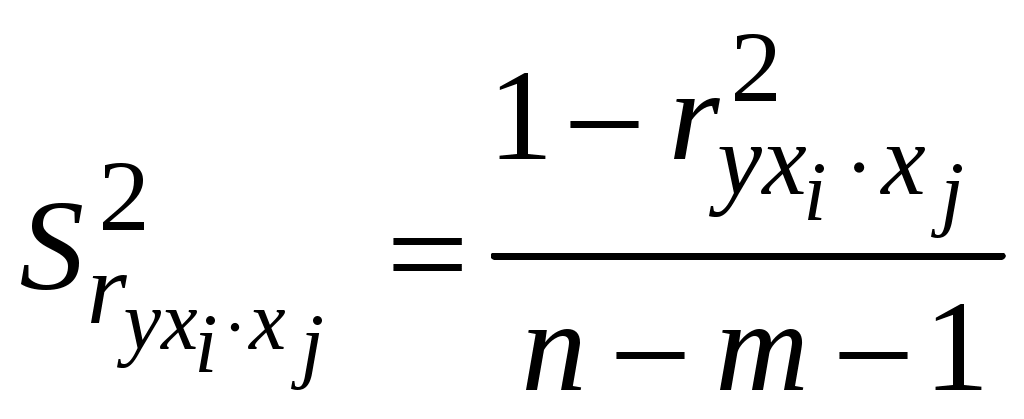 .Відповідно маємо: 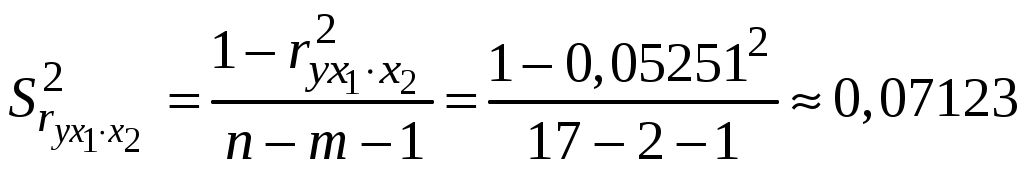 , 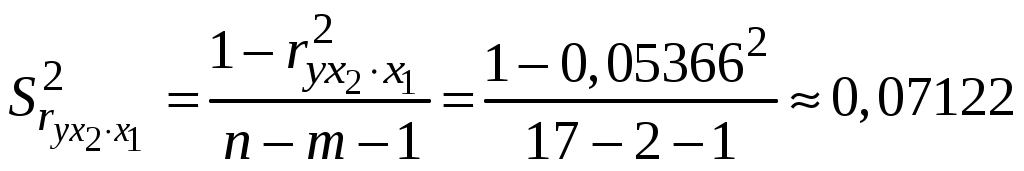.Тепер обчислимо емпіричне значення критерію Стьюдента: 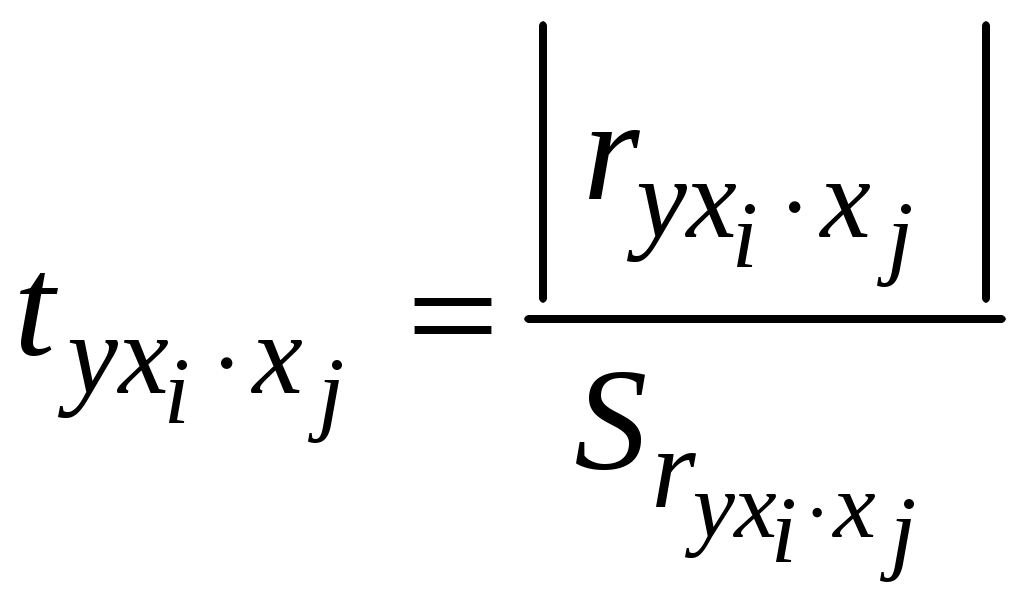 .Відповідно маємо: 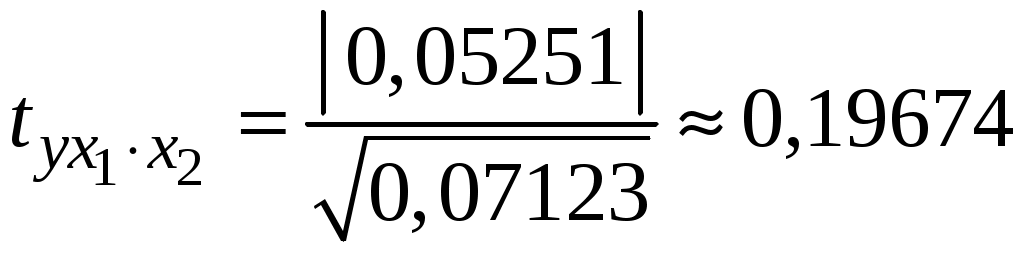 , 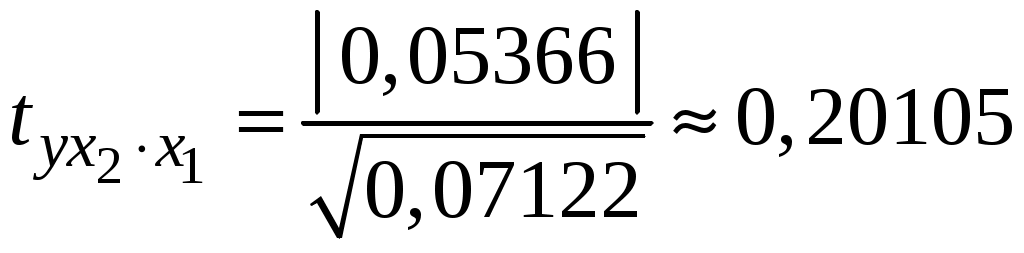.Для перевірки основної гіпотези щодо статистичної несуттєвості частинних коефіцієнтів кореляції визначаємо критичні точки розподілу Стьюдента для рівнів значущості  та  при кількості ступенів вільності  . За таблицею маємо:  та  . Оскільки для обох факторів X1 та X2 має місце співвідношення  , то з надійністю 95% вплив фондозабезпеченності та стажу роботи на продуктивність праці можна вважати статистично несуттєвим.Обчислимо коефіцієнт множинної кореляції:  .Визначимо коефіцієнт детермінації:  . Отже, на 0,56% мінливість продуктивності праці (Y) визначається мінливістю фондозабезпеченності (X1) та на стаж роботи (X2). Решта 99,44% обумовлені впливом факторів, які невраховані в даній моделі.Перевіримо значущість рівняння множинної регресії в цілому за допомогою F-критерію Фішера. Визначаємо емпіричне значення F-критерію Фішера за формулою: 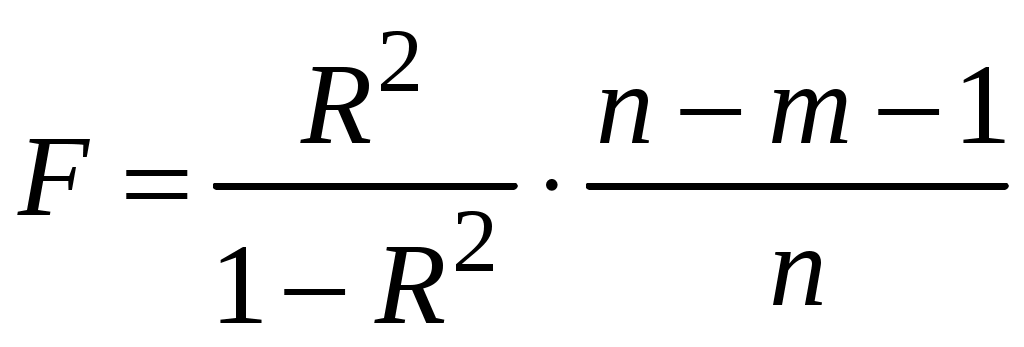 ,де n– обсяг вибіркової сукупності (кількість спостережень); m– кількість факторів, що розглядається;  – коефіцієнт детермінації.Підставивши відповідні значення, отримаємо результат: 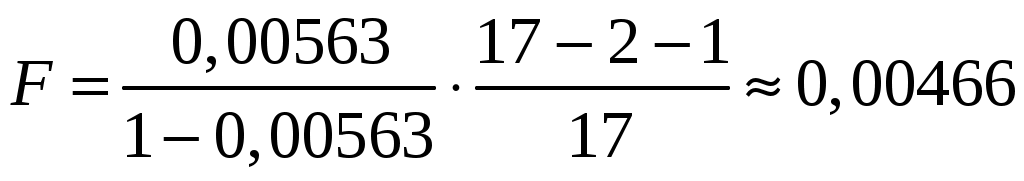 .Визначимо критичні значення розподілу Фішера для рівнів значущості та при кількості ступенів вільності  та  . За таблицею маємо  та  . Оскільки  , то з надійністю 95% можна стверджувати, що регресія в цілому є не значущою.Перевіримо доцільність присутності кожного з факторів економетричної моделі за допомогою частинних F-критеріїв: 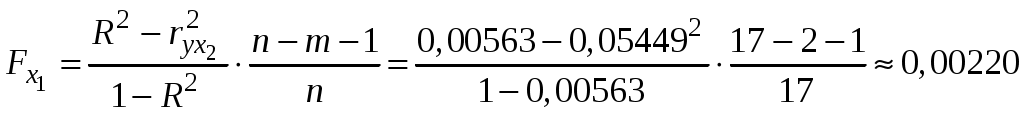 , 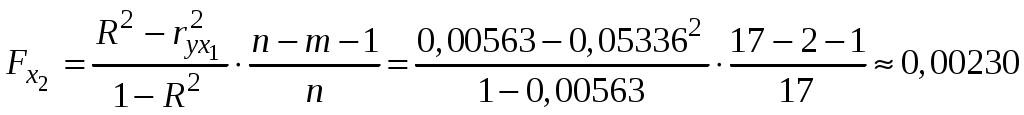.Порівняємо їх з критичними точками розподілу Фішера – Снедекора для рівнів значущості та при кількості ступенів вільності  та . За таблицею визначаємо:  та  . Для обох факторів X1 та X2 маємо, що  , тобто з надійністю 99% гіпотезу про відсутність впливу цих факторів на ознаку нема підстав відхилити. Відповідно його присутність в економетричні моделі є недоцільною, і фактор X1 можна виключити із аналізу. Це збігається з висновками, що були зроблені при перевірці за критерієм Стьюдента.Таким чином, для аналізу економічних процесів, що розглядаються, доцільно використовувати модель парної регресії, яка в стандартизованих змінних має вигляд:  .Після перетворення отримаємо модель у натуральних змінних:  . |
