КОНТР РАБ СТАТИСТИКА ДЕКАБРЬ 2015. Контрольная работа по дисциплине (модулю)
 Скачать 137.32 Kb. Скачать 137.32 Kb.
|
     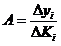 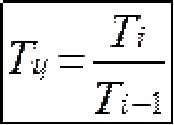 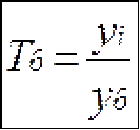 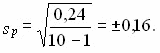 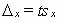 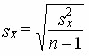 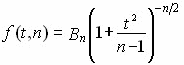 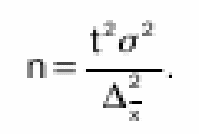 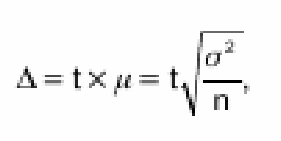 ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ КАЛУЖСКОЙ ОБЛАСТИ «КАЛУЖСКИЙ КОЛЛЕДЖ НАРОДНОГО ХОЗЯЙСТВА И ПРИРОДООБУСТРОЙСТВА» КОНТРОЛЬНАЯ РАБОТА № по дисциплине (модулю)_______________________________________ Выполнил (а): ____________________________________ студент (ка) _____ курса _______ группы по специальности _____________________ _____________________________________ заочной формы обучения шифр ____________ Проверил (а): ____________________________________ преподаватель: _______________________ ____________________________________ Калуга, 20___ г СОДЕРЖАНИЕВведение 4 1. Малая выборка в статистике 5 2. "Масштабные ориентиры" 11 3. Задача 14 Заключение 16 Список использованной литературы 17 ВведениеВыборочный метод - это такой статистический метод, при котором выводы и заключения о характеристиках генеральной совокупности делаются по ее выборке. Этот метод применяют тогда, когда исследовать всю генеральную совокупность или нецелесообразно из-за больших затрат времени и средств, или невозможно. Статистические характеристики для генеральной совокупности называются параметрами. Такие же характеристики для выборок называют оценками параметров или просто статистиками. Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 ≤ п ≤ 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц). Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика - это мера перевода числовой величины в графическую. Цель контрольной работы: рассмотреть малую выборку в статистике, дать определение понятию "масштабные ориентиры" и при помощи диаграммы изобразить данные по населению регионов России. 1. Малая выборка в статистикеЧтобы характеристики выборки с наибольшей точностью оценивали характеристики генеральной совокупности они должны быть: 2. Состоятельными 3. Несмещенными 4. Эффективными Состоятельная - это такая оценка, числовое значение которой с увеличением объема выборки стремится к числовому значению оцениваемого параметра. Несмещенная - это такая оценка, которая не имеет систематической погрешности, среднее значение которой при повторных многократных выборках из той же генеральной совокупности стремится к истинному значению оцениваемого параметра. Эффективная - это такая оценка, которая имеет наименьшую дисперсию относительно других оценок этого же параметра генеральной совокупности. Требования к выборкам. Выборки должны быть репрезентативными и случайными. Репрезентативность выборки означает, что ее состав и структура должны соответствовать составу и структуре генеральной совокупности из которой взята выборка. Случайность выборки состоит в том, что каждый вариант ( объект ) генеральной совокупности имел одинаковую вероятность и возможность попасть в выборку. Репрезентативность и случайность на практике обеспечиваются специальными методами отбора вариантов в выборку ( например, на основе таблицы случайных чисел ). По объему выборки делят на большие и малые. Большие выборки имеют объем более 30 вариантов ( n > 30 ). Малые выборки - это выборки объемом менее 30 вариантов ( n < 30 ). По принципу возврата вариантов в выборку их делят на бесповторные и повторные. Бесповторные - это такие выборки, в которых вариант после исследования в выборку не возвращается. Повторные выборки - такие, в которых вариант после исследования возвращается в выборку. Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Уменьшение стандартной ошибки выборки всегда связано с увеличением объема выборки. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки, соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем: откуда При случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия и дисперсии вариационного признака и обратно пропорционален квадрату предельной ошибки выборки. В частности, с увеличением предельной ошибки в 2 раза необходимая численность выборки может быть уменьшена в 4 раза. Из трех параметров два (коэффициент доверия и предельная ошибка выборке) задаются исследователем. При этом исследователь исходя из цели и задач выборочного обследования должен решить вопрос, в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта. В одном случае его может устраивать в большей мере надежность полученных результатов (t), нежели мера точности ( Д ), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает. В практике принято задавать величину предельной ошибки выборки в пределах до 10% предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по-разному: использовать данные подобных ранее проведенных об–следований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку. При проектировании выборочного наблюдения предполагаются заранее заданная величина допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения. В целом формула предельной ошибки выборочной средней позволяет решать следующие задачи: 1) определять величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности; 2) определять необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой, наперед заданной величины; 3) определять вероятность того, что в проведенной выборке ошибка будет иметь заданный предел. Малой выборкой принято считать выборку, объем которой варьируется в границах от 5 до 30 единиц. Малая выборка является единственным исследовательским приемом в тех случаях, когда организация сплошного или большого выборочного наблюдений невозможная. Преимущественно этим выборочным методом пользуются в случае исследования качества промышленной продукции, при установлении норм выработки. Однако, следует отметить, что необходимо быть осторожной при использовании малой выборки. Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п < \ 00 получается несоответствие между табличными данными и вероятностью предела; при п < 100 погрешность становится значительной. Несоответствие вызывается главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным. В выборках небольшого объема п ≤ 30 характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение. Использование малых выборок в ряде случаев обусловлено характером обследуемой совокупности. Так, в селекционной работе «чистого» опыта легче добиться на небольшом числе делянок. Производственный и экономический эксперимент, связанный с экономическими затратами, также проводится на небольшом числе испытаний. Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней. Плотность вероятностей распределения Стьюдента описывается функцией , (7.25) где t - текущая переменная; п — объем выборки; В — величина, зависящая лишь от п. Распределение Стьюдента имеет только один параметр: d.f. -число степеней свободы (иногда обозначается k). Это распределение, как и нормальное, симметрично относительно точки t = 0, но оно более пологое. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно располагать для определения искомой характеристики. Так, для расчета дисперсии должна быть известна средняя величина. Поэтому при расчете дисперсии d.f. = п - 1 Таблицы распределения Стьюдента публикуются в двух вариантах: 1) аналогично таблицам интеграла вероятностей приводятся значения t и соответствующие вероятности F(t) при разном числе степеней свободы; 2) значения t приводятся для наиболее употребляемых доверительных вероятностей 0,90; 0,95 и 0,99 или для 1 - 0,9 = 0,1, 1 - 0,95 = = 0,05 и 1 - 0,99 == 0,01 при разном числе степеней свободы. Такого рода таблица приведена в приложении (табл. 2), а также значение t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01. При малых выборках расчет средней возможной ошибки основан на выборочных дисперсиях, поэтому . Приведенная формула используется для определения предела возможной ошибки выборочного показателя: . Порядок расчетов тот же, что и при больших выборках. Пример. Для изучения интенсивности труда было организовано наблюдение за 10 отобранными рабочими. Доля работавших все время оказалась равной 0,40, дисперсия 0,4•0,6 = 0,24. По табл. 2 приложения находим для F(t) = 0,95 и d.f. = n - 1 = 9, t = 2,26. Рассчитаем среднюю ошибку выборки доли работавших все время: Тогда предельная ошибка выборки ?p = 2,26•0,16 = ± 0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах 39,64% ≤ ? ≤ 40,36% или 39,6% ≤ ? ≤ 40,4%. Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, то t было бы равно 1,96 и ?p - ± 0,31, т. е. доверительный интервал был бы несколько уже. Малые выборки широко используются для решения задач, связанных с испытанием статистических гипотез, особенно гипотез о средних величинах. Ряд динамики представляет собой ряд числовых значений определенного статистического показателя в последовательные моменты, или периоды времени. Числовые значения того или иного статистического показателя, составляющие динамический ряд, принято называть уровнями ряда. Абсолютный прирост рассчитывается как разность между двумя уровнями ряда, т.е. Y = Yi - Yi-1.Он показывает, на сколько единиц в абсолютном выражении уровень одного периода больше или меньше какого-то предыдущего уровня и, следовательно, может иметь знак <+> (при увеличении уровней) или <-> (при уменьшении уровней). Темп роста - относительный показатель (выражаемый в коэффициентах или процентах), получающийся в результате деления двух уровней, показывает, во сколько раз уровень данного периода больше или меньше базисного уровня или сколько процентов составил уровень данного периода по сравнению с базисным уровнем. В качестве базисного уровня (т.е. того уровня, с которым производится сравнение) в зависимости от цели исследования может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда) либо для каждого последующего предшествующий ему. Они могут быть рассчитаны следующими формулами:
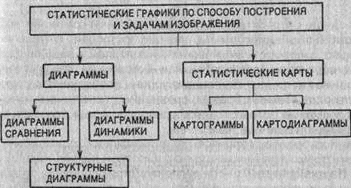
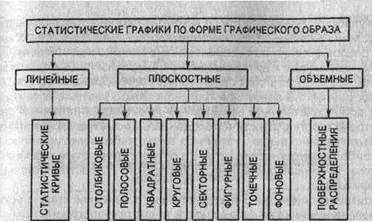
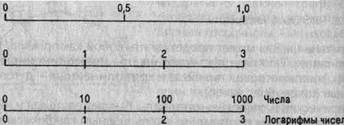
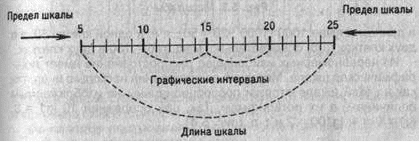
В первом случае говорят о базисных темпах роста, а во втором случае - о цепных темпах роста. Темп прироста - относительный показатель, показывающий, на сколько процентов один уровень больше (или меньше) базисного уровня. Этот показатель можно рассчитать путём вычитания 100% из темпа роста или как процентное соотношение абсолютного прироста к тому базисному уровню, по отношению, с которым абсолютный прирост рассчитан. Абсолютное значение одного процента прироста получается путем деления абсолютного прироста (цепного) на темп прироста (цепной) за соответствующий период 2. "Масштабные ориентиры"Масштабной шкалой называется линия, отдельные точки ко торой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике и включает три элемента: линию (или носитель шкалы), определенное число помеченных черточками точек, которые расположены на носителе шкалы в определенном порядке, цифровое обозначение чисел, соответствующих отдель ным помеченным точкам. Как правило, цифровым обозначением снабжаются не все помеченные точки, а лишь некоторые из них, расположенные в определенном порядке. По правилам числовое значение необходимо помещать строго против соответствующих точек, а не между ними (рис. 1). Рис. 1. Числовые интервалы Носитель шкалы может представлять собой как прямую, так и кривую линии. Поэтому различают шкалы прямолинейные (на пример, миллиметровая линейка) и криволинейные - дуговые и круговые (циферблат часов). Графические и числовые интервалы бывают равными и нерав ными. Если на всем протяжении шкалы равным графическим ин тервалам соответствуют равные числовые, такая шкала называ ется равномерной. Когда же равным числовым интервалам со ответствуют неравные графические интервалы и наоборот, шкала называется неравномерной. Масштабом равномерной шкалы называется длина отрезка (гра фический интервал), принятого за единицу и измеренного в каких-либо мерах. Чем меньше масштаб (рис. 2), тем гуще располагаются на шкале точки, имеющие одно и то же значение. Построить шкалу -это значит на заданном носителе шкалы разместить точки и обозначить их соответствующими числами согласно условиям задачи. Как правило, масштаб определяется примерной прикидкой возможной длины шкалы и ее пределов. Например, на поле в 20 клеток надо построить шкалу от 0 до 850. Так как 850 не делится удобрю на 20, то округляем число 850 до ближайшего удобного числа, Рис. 2. Масштабы в данном случае 1000 (1000 : 20 = 50), т. е. в одной клетке 50, а в двух клетках 100; следовательно, масштаб - 100 в двух клетках. Из неравномерных наибольшее распространение имеет лога рифмическая шкала. Методика ее построения несколько иная, так как на этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам. Так, при основании 10 1д1 = О-1д1 = 0 = 1; 1д100 = 2 и т. д. (рис. 3). Последний элемент графика - экспликация. Каждый график должен иметь словесное описание его содержания. Оно включа ет в себя название графика, которое в краткой форме передает его содержание; подписи вдоль масштабных шкал и пояснения к отдельным частям графика. Существует множество видов графических изображений (рис. 4). Их классификация основана на ряде признаков: а) способ построения графического образа; б) геометрические знаки, изображающие статистические показатели; в) задачи, решаемые с помощью графического изображения. Рис. 4. Классификация статистических графиков по форме графического образа По способу построения статистические графики делятся на диаграммы и статистические карты. Диаграммы - наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (простран ственном, временном и др.) независимых друг от друга величин: территорий, населения и т. д. Рис. 5. Классификация статистических графиков по способу построения и задачам изображения При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку Статистические карты - графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространенность статистических данных. Геометрические знаки как было сказано выше, - это либо точки, либо линии или плоскости, либо геометрические тела. В соответствии с этим различают графики точечные, линейные, плоскостные и пространственные (объемные). 3. ЗадачаПри помощи диаграммы изобразите данные по населению регионов России.
Найти % к общей численности населения? Решение: Тульская область. 803*100/1644=48,9 841*100/1644=51,1 Нижегородская область. 1790*100/2790=64,1 1000*100/2790=35,9 Московская обл. 3000*100/6030=49,8 3030*100/6030=50,2 Смоленская область. 653*100/1406=46,4 753*100/1406=53,6 Тверская область. 459*100/1050=43,7 591*100/1050=56,3 Рязанская область. 2300*100/4355=52,8 2055*100/4355=47,2 ЗаключениеТаким образом, малая выборка – это не сплошное статистическое наблюдение, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Обычно объем малой выборки не превышает 30 единиц, а минимальный объем может доходить до 4-5 единиц. В отдельных случаях к малой может быть отнесена выборка до 45 единиц. Малая выборка широко применяется в экономических исследованиях и при организации контроля качества товаров и услуг. Масштабные ориентиры графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шкал. Список использованной литературы
| ||||||||||||||||||||||||||||||||||||||||||||||||
