работа по статистике. 3 вар. Контрольная работа 01 10. Найти доверительный интервал для оценки математического ожидания а
 Скачать 98.39 Kb. Скачать 98.39 Kb.
|
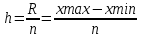 h(7) = 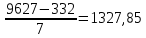
В) 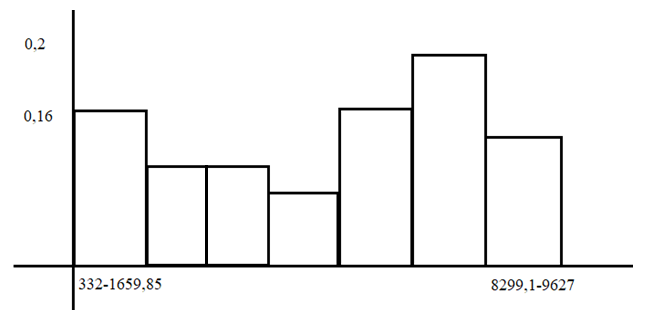 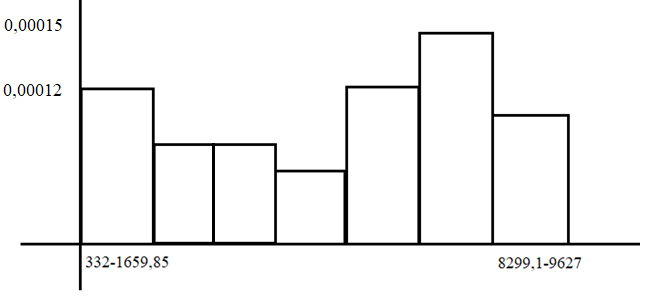 г) Средняя взвешенная (выборочная средняя) 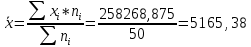 Дисперсия 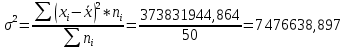 д) Степень асимметрии As = 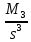 M3 = 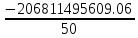 = -4136229912.18 = -4136229912.18σ = 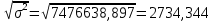 As = 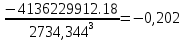 эксцесс Ex = 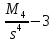 = = 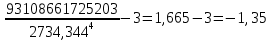 е) 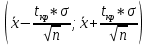 Так как n > 30, то определяем значение tкр по таблице Лапласа 2Ф(tkp) = γ Ф(tkp) = 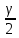 = = 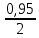 = 0,475 = 0,475По таблице Лапласа найдем значение Ф(tkp) = 0.475 tkp(γ) = 1.96 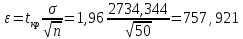 ( 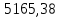 – 757,921; – 757,921; 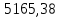 + + 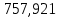 ) = (4407,459; 5923,301) ) = (4407,459; 5923,301)ж) Критерий Пирсона 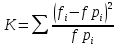 Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа 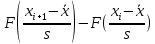 где s = 2734.344, xср = 5165.38 Теоретическая (ожидаемая) частота равна fi = fpi, где f = 50 Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1)
Критическая область для этой статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и значениям s, k, r=2 Kkp = χ2(7-2-1;0.05) = 9.48773; Kнабл = 15.62 Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу |
