Контрольная работа № 4.
8.01-8.10. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0.95, зная выборочную среднюю 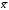 , объем выборки n и среднеквадратичное отклонение s. , объем выборки n и среднеквадратичное отклонение s.
Задачи
|
8.01
|
8.02
|
8.03
|
8.04
|
8.05
|
8.06
|
8.07
|
8.08
|
8.09
|
8.10
|
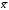
|
75.08
|
75.17
|
75.10
|
75.15
|
75.12
|
75.13
|
75.14
|
75.11
|
75.16
|
75.09
|
n
|
225
|
36
|
169
|
64
|
121
|
100
|
81
|
144
|
49
|
169
|
s
|
15
|
6
|
13
|
8
|
11
|
10
|
9
|
12
|
7
|
13
|
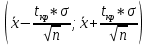
Так как n > 30, то определяем значение tкр по таблице Лапласа
2Ф(tkp) = γ
Ф(tkp) = 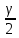 = = 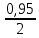 = 0,475 = 0,475
По таблице Лапласа найдем значение Ф(tkp) = 0.475
tkp(γ) = 1.96
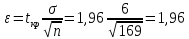
(75,1 – 1,96; 75,1 + 1,96) = (73,14; 77,06)
8.11-8.20. В табл. 1. Приведены результаты измерения некоторой физической величины.
а) Упорядочить выборку в порядке возрастания (построить вариационный ряд).
б) Построить группированные выборки для 4, 5и 6 интервалов.
в) Построить для этих трёх выборок полигоны и гистограммы абсолютных частот.
г) Построить для этих трёх выборок полигоны и гистограммы относительных частот.
д) Найти оценки для математического ожидания а и дисперсии s 2 отдельно по каждой из группированных выборок.
Таблица 1.
8.11
|
8.12
|
8.13
|
8.14
|
8.15
|
8.16
|
8.17
|
8.18
|
8.19
|
8.20
|
110,6
|
125,5
|
133,8
|
140,1
|
148,1
|
158,4
|
170,4
|
181,4
|
192,2
|
197,8
|
110,1
|
120,0
|
127,4
|
142,9
|
153,9
|
159,3
|
171,8
|
178,6
|
189,0
|
198,5
|
111,5
|
116,0
|
128,0
|
138,6
|
149,3
|
164,5
|
172,3
|
181,4
|
185,9
|
202,8
|
111,7
|
120,2
|
129,5
|
137,9
|
144,1
|
158,1
|
172,4
|
179,7
|
189,0
|
206,4
|
106,6
|
120,9
|
130,3
|
137,5
|
151,3
|
158,6
|
176,3
|
177,2
|
192,0
|
198,1
|
110,9
|
119,2
|
131,3
|
137,4
|
145,6
|
156,0
|
170,4
|
181,7
|
187,1
|
198,3
|
113,4
|
122,5
|
127,5
|
134,2
|
151,0
|
161,6
|
168,5
|
181,2
|
191,6
|
194,3
|
108,2
|
121,8
|
132,6
|
139,8
|
148,0
|
159,9
|
174,1
|
178,8
|
188,6
|
196,4
|
107,0
|
116,0
|
127,1
|
142,6
|
148,0
|
162,9
|
167,2
|
182,4
|
185,3
|
197,8
|
114,4
|
117,8
|
126,4
|
136,7
|
149,9
|
159,8
|
169,7
|
182,6
|
187,9
|
199,2
|
107,7
|
121,7
|
132,9
|
137,4
|
144,9
|
159,2
|
167,3
|
182,2
|
191,5
|
203,5
|
109,6
|
118,4
|
132,8
|
139,7
|
152,0
|
163,0
|
175,4
|
179,0
|
188,0
|
199,7
|
111,3
|
121,6
|
127,9
|
141,4
|
150,0
|
161,5
|
170,4
|
183,7
|
190,8
|
203,5
|
111,7
|
122,6
|
128,6
|
133,1
|
149,1
|
171,0
|
166,8
|
186,5
|
187,6
|
193,0
|
110,6
|
123,3
|
133,4
|
144,6
|
150,2
|
160,1
|
169,8
|
179,2
|
186,9
|
202,6
|
105,8
|
120,4
|
125,6
|
142,7
|
153,3
|
160,2
|
169,5
|
181,7
|
190,0
|
199,1
|
113,2
|
115,6
|
133,9
|
136,3
|
150,6
|
165,7
|
171,2
|
183,9
|
190,4
|
205,3
|
110,6
|
118,7
|
127,3
|
138,6
|
149,1
|
158,7
|
172,1
|
177,0
|
190,4
|
194,0
|
107,2
|
120,2
|
126,2
|
135,9
|
151,0
|
165,8
|
163,3
|
182,5
|
189,8
|
198,4
|
107,1
|
120,0
|
131,5
|
137,5
|
153,0
|
157,4
|
168,1
|
178,8
|
188,9
|
199,2
|
103,7
|
127,4
|
130,9
|
144,0
|
153,9
|
161,1
|
170,9
|
179,3
|
190,7
|
199,3
|
106,0
|
122,1
|
128,1
|
135,8
|
146,7
|
161,7
|
169,1
|
179,6
|
194,8
|
200,7
|
108,6
|
119,3
|
132,7
|
138,7
|
148,5
|
160,8
|
168,4
|
181,7
|
194,3
|
202,7
|
107,3
|
119,4
|
129,0
|
140,8
|
148,0
|
158,5
|
168,9
|
184,4
|
194,2
|
199,4
|
113,7
|
118,8
|
133,8
|
139,9
|
148,9
|
163,7
|
169,0
|
182,4
|
191,2
|
197,2
|
8.11
|
8.12
|
8.13
|
8.14
|
8.15
|
8.16
|
8.17
|
8.18
|
8.19
|
8.20
|
а)
125,6
|
130,3
|
126,2
|
130,9
|
126,4
|
131,3
|
127,1
|
131,5
|
127,3
|
132,6
|
127,4
|
132,7
|
127,5
|
132,8
|
127,9
|
132,9
|
128,0
|
133,4
|
128,1
|
133,8
|
128,6
|
133,8
|
129,0
|
133,9
|
129,5
|
|
Б) Шаг интервала по формуле Стерджесса
|
 Скачать 98.39 Kb.
Скачать 98.39 Kb.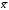 , объем выборки n и среднеквадратичное отклонение s.
, объем выборки n и среднеквадратичное отклонение s.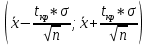
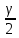 =
= 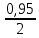 = 0,475
= 0,475