контр_раб_1_образец. Контрольная работа 1 1 " Механика, молекулярная физика, термодинамика " Вариант Студент З. О, гр. Ас 568
 Скачать 58.91 Kb. Скачать 58.91 Kb.
|
    Министерство образования Республики Беларусь Министерство образования Республики БеларусьУчреждение образования Брестский государственный технический университет Кафедра физики Контрольная работа № 1 №1 "Механика, молекулярная физика, термодинамика" Вариант __________ Выполнил: Студент З.О, гр. АС 568 _________________ Проверил: Ворсин Н.Н. Брест 2015 Задача 1. Кинематика, динамика и законы сохранения Дано: m1=7,0кг; m2=0,80кг; m3=5,5кг; m4=3,4кг; α=30º μ=0,40; r3=0.55 м r4=0,55м; R4=1,25м; τ=0,55с Т2 Т1 Система, показанная на рисунке, состоит из грузов массами m1 и m2, которые движутся поступательно. К грузам прикреплены невесомые нерастяжимые нити, перекинутые или намотанные на блоки массами m3 и m4, которые могут без трения вращаться вокруг горизонтальных осей. Блок массой m3 – сплошной цилиндр, а блок массой m4 – ступенчатый цилиндр с радиусами степеней r4 и R4 и одинаковой высотой (рисунок 1.10). При движении нити по блокам не проскальзывают, участки нитей для тел на наклонных плоскостях параллельны этим плоскостям, коэффициент трения тел о любую плоскость равен μ. Система начинает движение из состояния покоя. Считая, что все нити и участки плоскостей имеют достаточную длину, выполнить следующие задания: 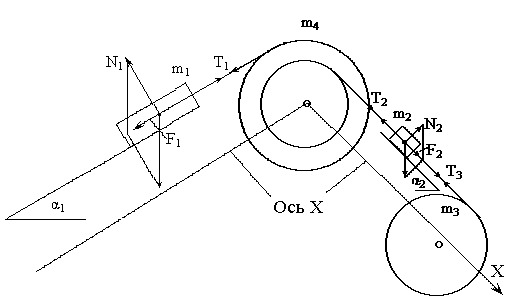 m1=7,0кг; m2=0,80кг; m3=5,5кг; m4=3,4кг; α=30º μ=0,40; r4=0,55м; R4=1,25м; τ=0,55с 1). Найти ускорения грузов массами m1 и m2 и угловые ускорения блоков ε3, ε4. Принять r3=r4. 2). Найти силы натяжения всех нитей. 4). Используя кинематические формулы, найти скорости грузов, угловые скорости блоков и пути, пройденные грузами спустя время τ после начала движения. 7). Используя закон изменения механической энергии, найти другим способом скорости грузов и угловые скорости блоков в тот момент, когда пути, пройденные грузами, составят значения, найдены в п. 4. Решение: 1-2,. Найдем ускорения масс в системе и силы натяжения нитей. Определим направление движения системы, которая находится од действием сил тяжести грузов m1 и m2. Момент силы m2g на блоке 4 равен, m2gr4sin(α+15o)= 0,80кг*10м/с2*0,55м /√2=6.25Нм. Момент силы от массы m1 на том же блоке равен m1gsin(α)R4 оказывается существенно больше. Следовательно, груз m2 будет двигаться вверх, а m1 - вниз по наклонным плоскостям. При этом сила трения будет действовать против движения, т.е. будет прибавляться к скатывающей силе второго груза и вычитаться из скатывающей силы первого груза. Для сокращения записей введем следующие обозначения: равнодействующая силы тяжести груза m1, реакций опор - N1, силы трения первого груза о наклонную плоскость обозначена F1. Равнодействующая соответствующих сил второго груза обозначена F2. Векторы этих сил показаны на рисунке, а их модули можно вычислить отдельно F1=m1gsin(α1)-m1gcos(α1)μ1 : F2=m2gsin(α2)+m2gcos(α2)μ2. Вычислим моменты инерции блоков: 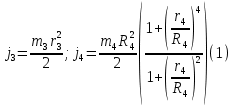 Коэффициент в больших скобках обозначим k4. Составим векторные уравнения движения для всех масс рассматриваемой системы: 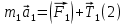 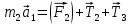 Составим уравнения вращательного движения блоков. Моменты сил, действующих на блоки, представим в виде векторных произведений радиус-векторов на силы. 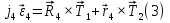 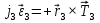 Проведем кривую ось Х, показанную на рисунке. На нее будем проецировать векторы сил и линейных ускорений. Все эти векторы коллинеарные (параллельны) выбранной оси, так что проекции будут равны модулем с определенным знаком. 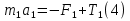 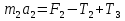 Аналогично спроецируем на другую осьуравнения вращательных движений блоков. Эту ось выбираем параллельно осям вращения, т.е. перпендикулярно плоскости чертежа в направлении от нас к чертежу. При этом проекция момента, вращающего блок по часовые стрелке будет положительна, а против часовой стрелки - отрицательна: 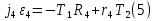 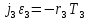 Мы имеем неизвестных: Т1, Т2, Т3, а1, а2, ε4, ε3, всего 7 неизвестных. Число уравнений для их вычисления также должно быть равно 7. Следовательно, необходимы еще 3 кинематических соотношения. Это уравнения, связывающие линейные и угловые ускорения: 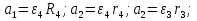 (6) (6)В результате получаем систему из 7 уравнений с 7 неизвестными величинами. После ее решения будем иметь 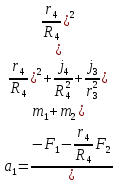 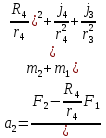 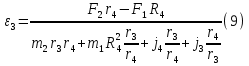 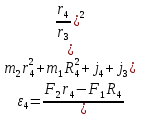 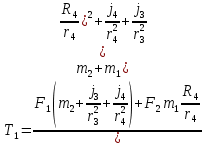 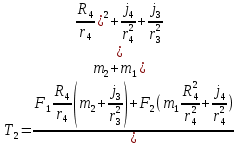 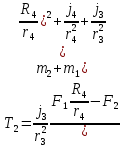 После подстановки числовых данных получим: а1=-0.775м/с2; а2=-0.341м/с2; ε3=-0.62рад /с2; ε4=-0.62рад/с2; Т1=5.092Н; Т2=8.97Н; Т3=0.938Н. Первые впечатления от полученного решения. Все ускорения получились отрицательными. Это означает что поступательное движение грузов происходит против положительного направления выбранной для проецирования оси. Аналогичный вывод и для угловых ускорений, их векторы направлены против выбранной оси, т.е. от рисунка к нам. Силы натяжения нитей получились положительными. В действительности каждая из них - это пара сил, растягивающих нить в противоположные стороны. Таким образом, полученные ответы правдоподобны. Пункты 1, 2 выполнены. 4. Определим скорости грузов, угловые скорости блоков и пути, пройденные грузами за время τ после начала движения. Движение всех масс рассматриваемой системы будет равноускоренным. Начальные скорости равны нулю. Поэтому скорости определятся как произведения соответствующих ускорений на время движения. v1=a1*τ=-0.775м/с2*0.55c=-0,42625м/с v2=a2*τ=-0.341м/с2*0.55c=-0,18755м/с ω3=ε3*τ=-0.62рад/с2*0.55с=-0,341рад/с ω4=ε4*τ=-0.62рад/с2*0.55с=-0,341рад/с Пройденные пути определятся по формулам равноускоренного движения: S1=a1τ2/2==-0.775м/с2*0,3025c2=-0,2344375м S2=a2τ2/2=-0.341м/с2*0,3025c2=-0,2344375м=-0,1031525м Угловые пути – это углы на которые повернутся блоки: ��3=��4= ε3τ2/2=-0.62рад /с2*0,3025c2=-0,18755рад Пункт 4 выполнен. 7. Используя закон изменения механической энергии найти другим способом скорости грузов и угловые скорости блоков в заданной точке их движения. Допустим, что к какому-то моменту времени t после начала движения первый груз прошел путь s1. При этом он опустился по вертикали на высоту h1=s1*sin(α1). Поскольку грузы m1 и m2 связаны нерастяжимой нитью, второй груз пройдет путь s2=s1*r4/R4 и поднимется на высоту h2=s2*sin(α2) =s1*r4*sin(α2) /R4. Изменение потенциальной энергии грузов равно ΔU=m1*g*h1-m2*g*h2. Часть этой разностной энергии превратится в работу по преодолению трения, а оставшаяся часть - в кинетическую энергию грузов и блоков. Выразим все энергии и работы через ускорение первого груза и время движения. Это позволит получить уравнение для а1, а не систему 7 уравнений с 7 неизвестными. Перемещение первого груза s1=a1t2/2. Высота, на которую он опустится h1=sin(α1)*( a1t2/2). Путь второго груза s2=s1*r4/R4 и высота, на которую он поднимется h2= sin(α2)* (a1t2/2)*r4/R4 Освободившееся потенциальная энергия ΔU=m1g sin(α1)*( a1t2/2) - m2g*sin(α2)* (a1t2/2)*r4/R4= g*( a1t2/2)*(m1* sin(α1)- m2*sin(α2)* r4/R4) Кинетическая энергия первого груза Т1=m1v12/2=m1a12t2/2 Кинетическая энергия второго груза Т2=m2v22/2=m2a12t2r42/(2R42) Кинетическая энергия блока m3: T3=j3ω32/2=j3a12t2r42/(2r32R42) Кинетическая энергия блока m4: T4= j4ω42/2=j4a12t2/(2R42) Работа сил трения первым грузом: A1=Fтр1s1=m1gcos(α1)μ1a1t2/2 Работа сил трения второго груза А2= Fтр2s2= m2gcos(α2)μ2 a1t2r4/(2R4) Теперь приравняем изменение потенциальной энергии системы тел к затраченной работе по преодолению сил трения и кинетической энергии, приобретенной телами.  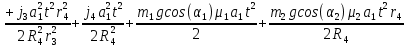 Сократив на а1t2 левую и правую части, можем выразить а1 следующей формулой: 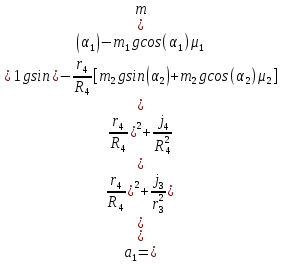 С точностью до обозначений и знака получилась такая же формула как от решения системы уравнений. Это естественно, поскольку закон сохранения механической энергии выводится из тех же соотношений механики, которые дают систему уравнений для движения тел. Имея а1, можем получить величины других неизвестных 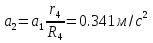 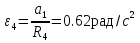 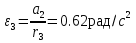 Пункт 7 выполнен. 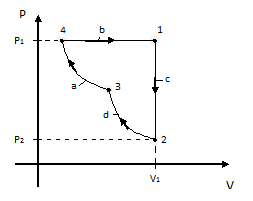 Задача 3. Молекулярная физика и термодинамика. На рисунке показан цикл, осуществляемый со смесью, состоящей из газа 1 - гелия массой m1 и газа 2 – хлора массой m2, которые считаются идеальными. Цикл состоит из четырех процессов: а – изотерма, b – изобара, с – изохора, d – адиабата. Цикл показан на (PV)-диаграмме, значения Р1, Р2 и V1 заданы в таблице. Выполнить следующие задания:
Для сокращения записей удобно использовать понятие «количество вещества» или, что тоже самое – количество молей ν=m/M вещества – это отношение массы вещества к его молярной массе. При таком обозначении уравнение состояния – уравнение Менделеева – Клапейрона запишется в виде: 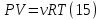 Мы имеем для гелия ν1=m1/MHe=2 моль, ν2=m2/2MCl=0.5 моль. Двойка в знаменателе последней формулы обусловлена тем, что хлор двухатомный газ и масса молекулы вдвое превосходит массу атома. Эквивалентную молярную массу определим из закона Дальтона: давление газовой смеси равно сумме давлений компонентов смеси. Сложим уравнения Менделеева – Клапейрона, записанные для компонентов смеси? 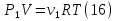 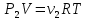 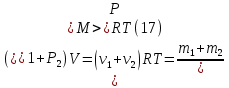 Через 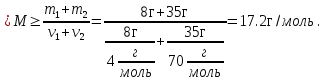 представляет собой эквивалентную молярную массу смеси. Эквивалентное число степеней свободы, которое обозначим через i, определится из формулы приращения внутренней энергии изохорного нагрева: 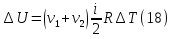 Это приращение естественно равно сумме приращений внутренних энергий составляющих смесь газов: 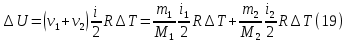 Рассматривая это равенство как уравнение для i, получим: 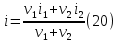 Наша смесь состоит из 2 молей одноатомного газа – гелия и полумоля двухатомного газа – хлора. Отношение (m/M) представляет собой число молей. Следовательно, i1=2 мол, i2=1 моль. После подстановки получим: 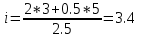 Показатель адиабаты – это отношение молярных теплоемкостей нагрева при постоянном давлении и постоянном объеме: 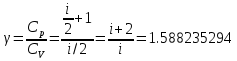 Первый пункт выполнен
В нашем случае не заданы параметры точки 3, в которой стыкуются адиабата и изотерма. Зададим положение этой точки условием V3=V2/1.5. В исходной точке (1) давление и объем заданы, температура определится уравнением состояния: 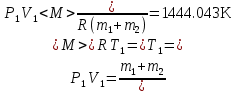 Запишем уравнения процессов: Участок 1-2 Изохора. Уравнение P1Т2=P2Т1. Из этого равенства определится температура второй точки Т2=Т1*P2/P1= 601.68 К; Участок 2-3. Адиабата. Уравнение 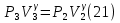 Поскольку V3=V2/1.5=33.333 л, будем иметь P3=P2*1.5γ=250Кпа*1.5γ= 4.76*105Па. Температура в точке диаграммы 3 найдется из уравнения состояния 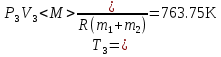 Участок 3-4. Изотерма Т4=Т3, Уравнение: PV=const Кроме того, по графику цикла Р4=Р1. Определится объем V4=P3V3/P1= 26.44л Участок 4-1 – изобара, которая свяжет параметры V4, T4 c V1, T1 следующим уравнением V4=V1*T3/T1. Поскольку все члены этого равенства уже вычислены ранее, его можно рассматривать как проверку полученных значений. Поместим для наглядности параметры состояний газа в точках 1, 2, 3, 4 в следующую таблицу.
Пункт 2 выполнен.
Давление каждой из компонент смеси определятся уравнением Менделева – Клапейрона, записанного для угловых точек цикла  Аналогично для других угловых точек. Пункт 3 выполнен.
Термодинамическая температура смеси уже вычислена во всех угловых точках цикла, ее значения представлены в таблице. 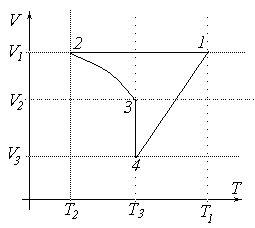 На рисунке показан рассматриваемый цикл в координатах Р-Т. Он включает в себя изохорическое расширения – участок 1-2, адиабатическое сжатие – участок 2-3, изотермическое сжатие – участок 3-4, изобарическое расширение – участок 4-1. На участке 2-3 зависимость давления от температуры нелинейна. 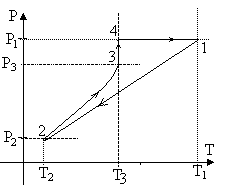 Аналогично можно изобразить цикл в координатах V-T. Пункт 4 выполнен.
В процессе изохорного охлаждения (участок 1-2) работа не совершается, газ отдает внутреннюю энергию, которая получит отрицательное приращение на величину 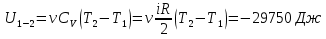 Адиабатическое сжатие на участке 2-3 сопровождается превращением работы внешних сил во внутреннюю энергию газовой смеси, которая получит положительное приращение: 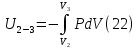 Давление и объем в адиабатическом процессе связаны соотношением PVγ=A, шде А – константа, которую можно определить в начальной точке участка: A= P2V2γ. В результате мы получим: 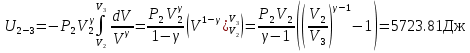 На участке изотермического сжатия 3-4 внутренняя энергия смеси не изменяется U3-4=0. На последнем участке цикла 4-1 происходит изобарическое расширение, смесь совершает работу. Кроме того, на этом участке газовая смесь подогревается, вследствие чего температура ее не уменьшается, а увеличивается. Приращение внутренней энергии равно 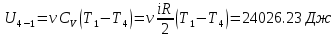 Легко сделать проверку вычислений. Сумма изменений внутренней энергии на всех участках замкнутого цикла должна равняться нулю: U12+U23+U41=0.04 Дж Небольшое отличие от нуля обусловлено округлениями результатов вычислений. Пункт 5 выполнен.
Подсчитаем совершенную за цикл механическую работу:  Первое слагаемое – это работа на участке изобарического расширения (4-1). Второе слагаемое отрицательно, поскольку на участке 2-3 внешние силы совершают работу над газовой смесью, сжимая ее. Эта работа целиком уходит на увеличение внутренней энергии смеси. Третье слагаемое также отрицательно, так как на участке 3-4 внешние силы изотермически сжимают смесь. На данном участке (3-4) PV=A, где константа А определится в какой-либо точке участка, например, в начальной: A=P3V3. Тогда 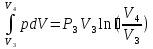 Механическая работа, совершенная за один цикл газовой смесью будет равна: 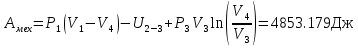 В ходе цикла газовая смесь получает от нагревателя тепло при изобарическом расширении на участке 4-1. Полученное тепло можно вычислить по формуле изобарического процесса Q41=Cp*ν*(T1-T4) = 38159.312 Дж На остальных участках смесь тепла не получает. КПД цикла будет равно 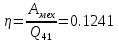 КПД цикла Карно при температуре нагревателя Т1 и температуре холодильника Т2 будет равен: 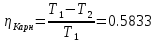 Естественно, КПД идеального цикла оказался существенно больше. Пункт 6 выполнен. |