математика. Контрольная работа 1 Дифференциальные уравнения. Интегральные исчисления по дисциплине Математика Томск 2022
 Скачать 271 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Контрольная работа №1 Дифференциальные уравнения. Интегральные исчисления по дисциплине «Математика» Томск 2022 Вариант 1.9.Найти неопределённые интегралы 1.  . Решение. Для вычисления данного интеграла необходимо сделать замену  . После подстановки в интеграл получим: 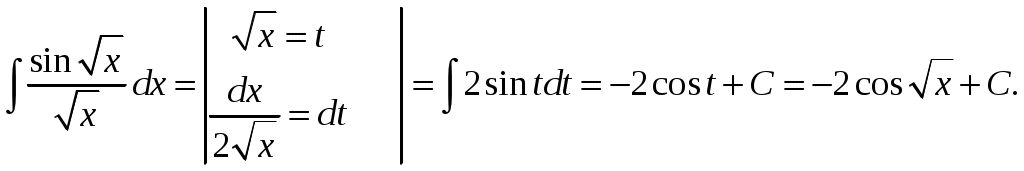 2.  ;Решение. Для вычисления данного интеграла необходимо сделать замену  . После подстановки в интеграл получим: 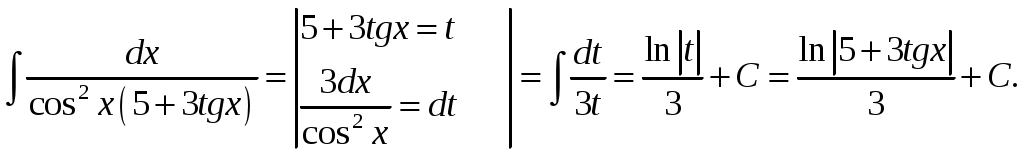 3.  ;Решение. Для вычисления данного интеграла необходимо сделать замену  . После подстановки в интеграл получим:  4.  ; Решение. Для вычисления данного интеграла необходимо сделать замену  . После подстановки в интеграл получим: 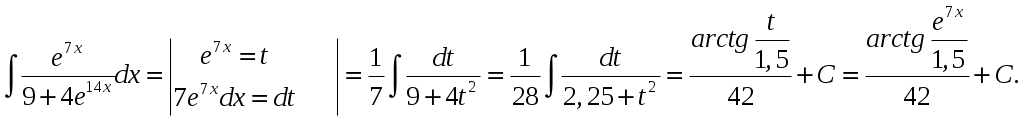 5.  ; Решение. Применим формулу интегрирования по частям 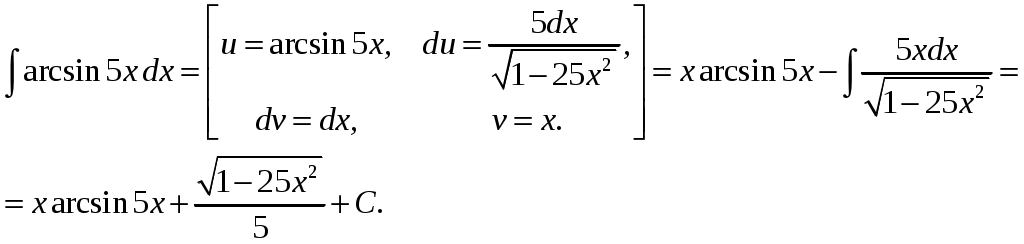 .  6.  ;Решение. 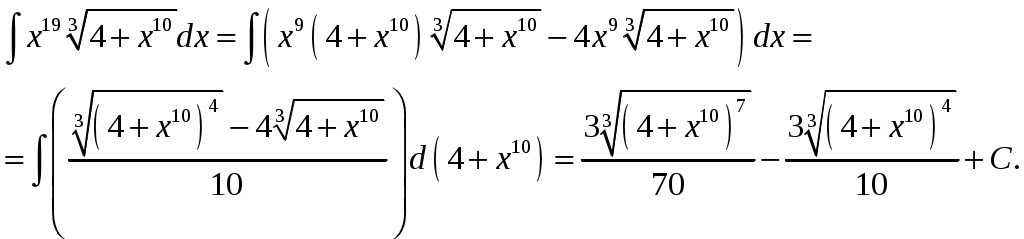 7.  ;Решение. Применим подстановку 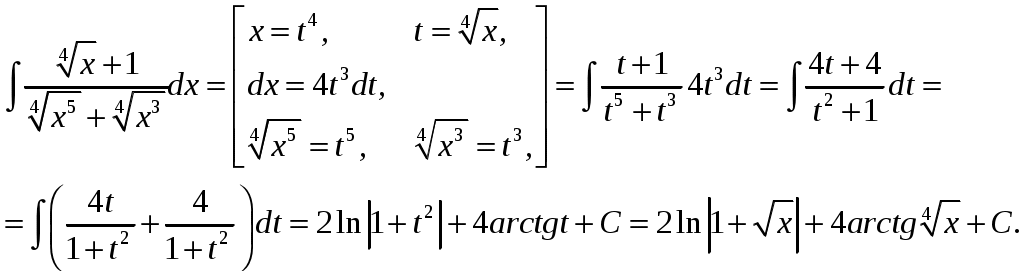 . Получим 8.  ; Решение. 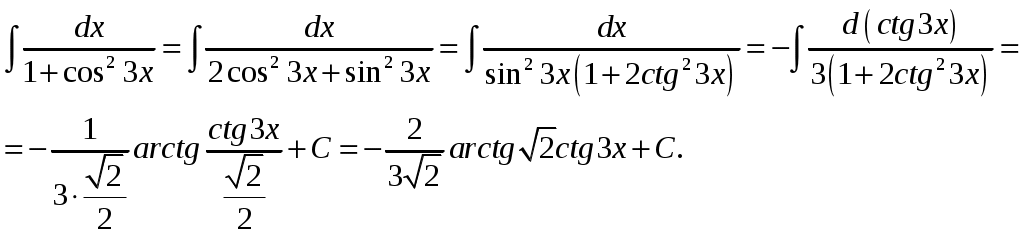 9. 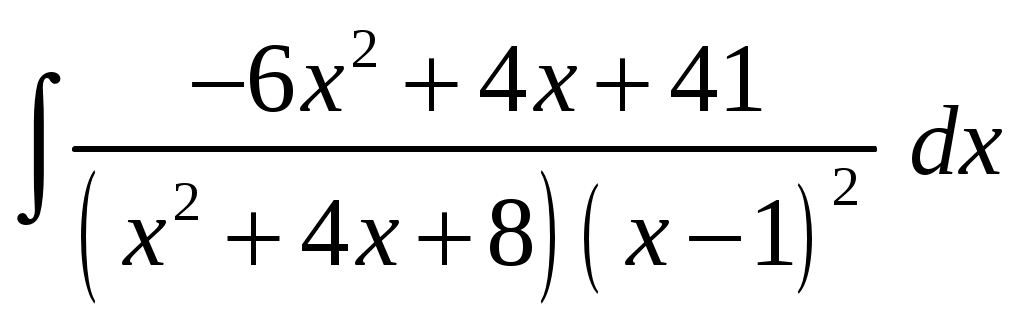 ;Решение. Разложим подынтегральную функцию на сумму простейших дробей: 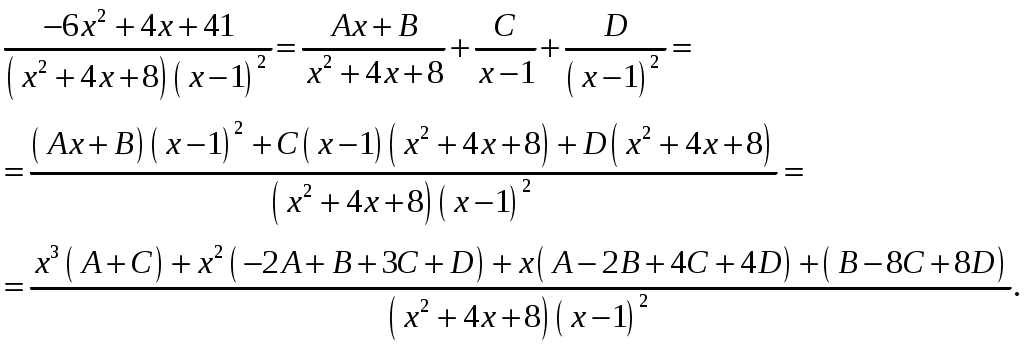 Коэффициенты  , найдем из условия: . Приравняем коэффициенты с одинаковыми степенями при х: 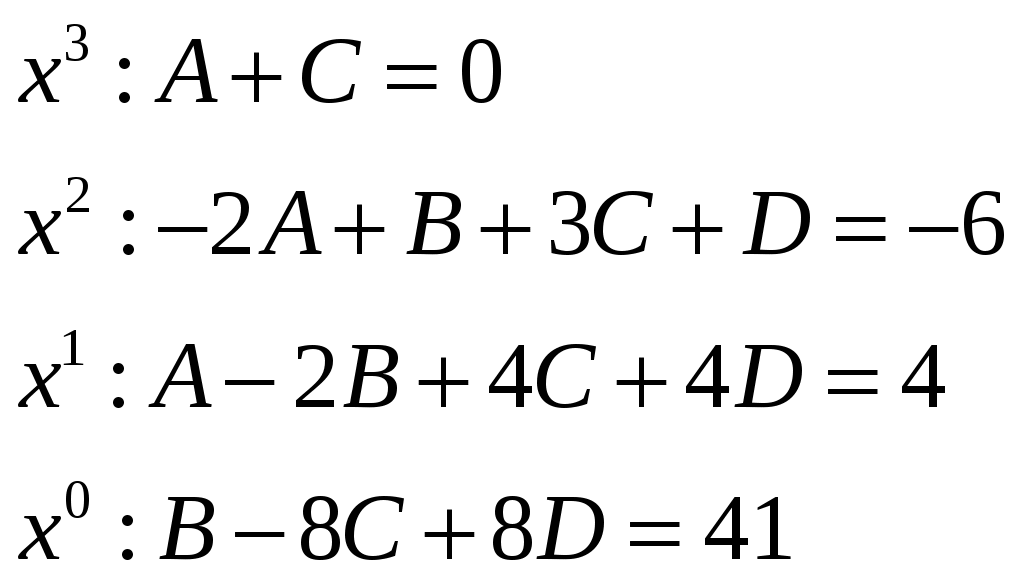 откуда  Таким образом, 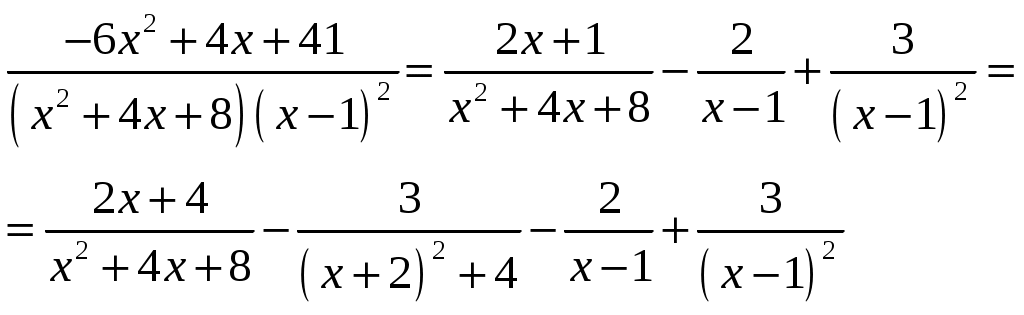 . 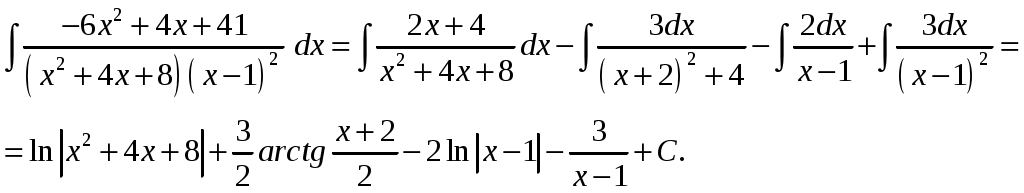Вычислить определённые интегралы 10. 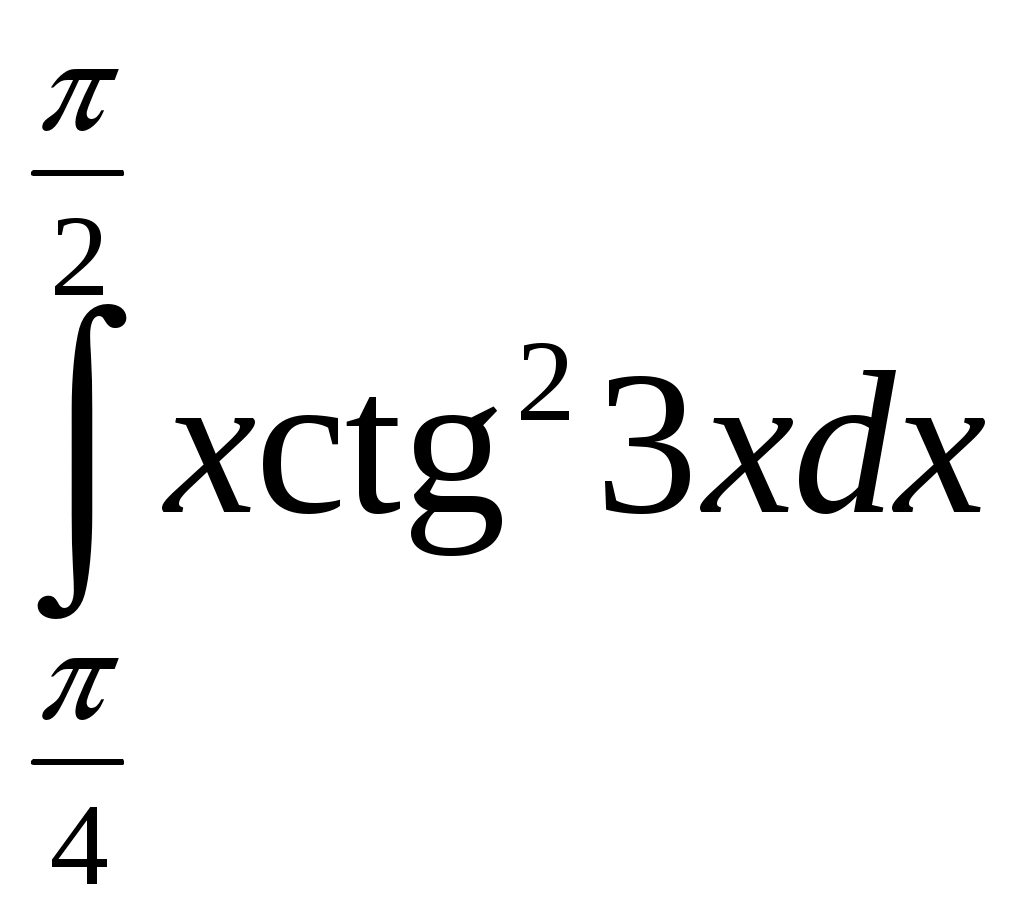 ; Решение. Применим формулу интегрирования по частям 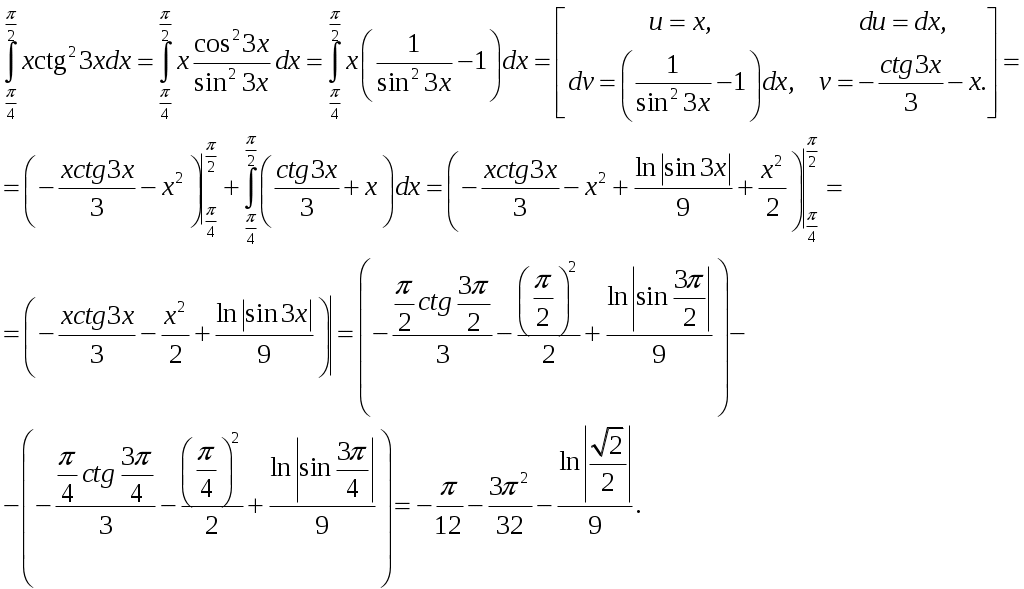.  Ответ: 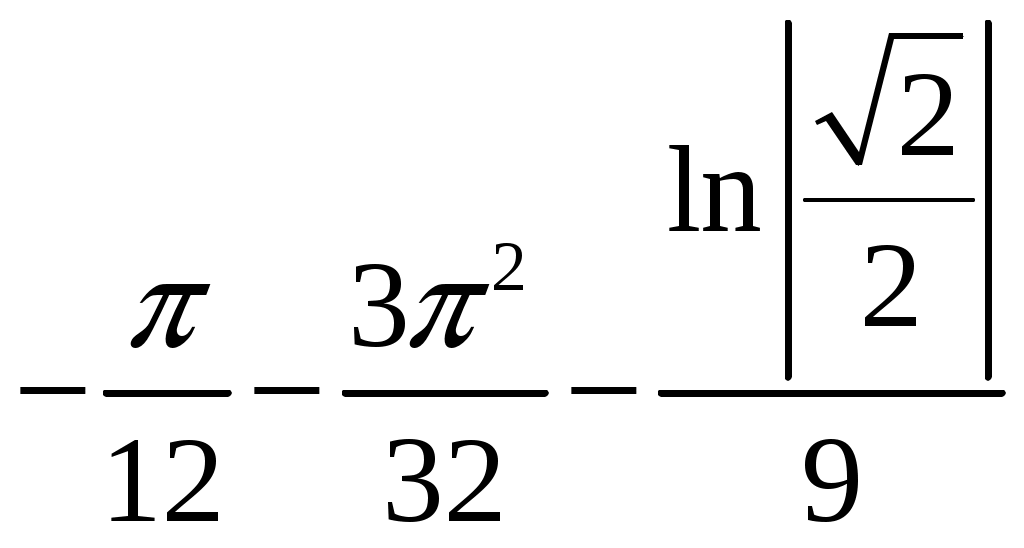 .11. 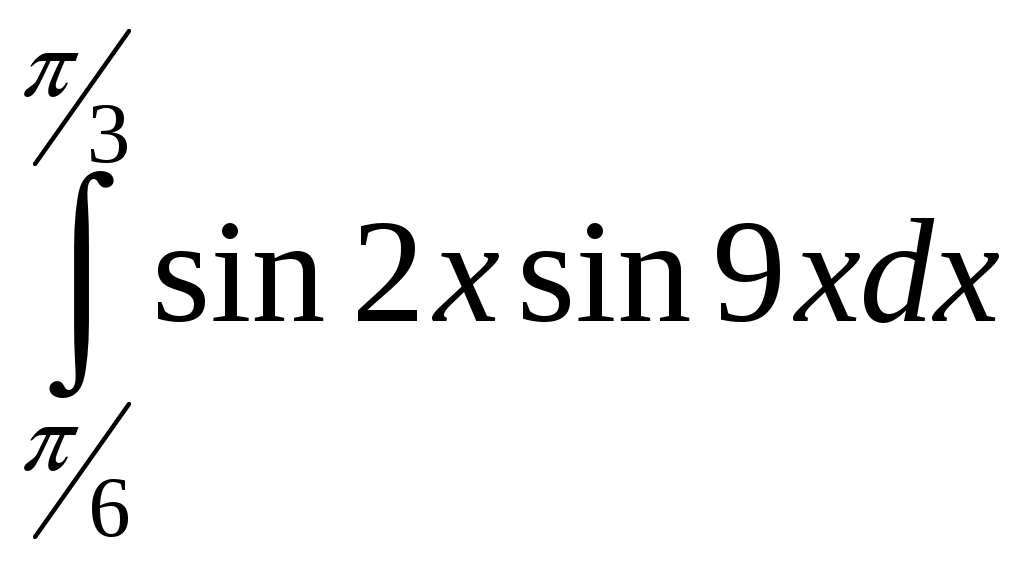 .Решение. Применим тригонометрическую формулу произведения синусов: 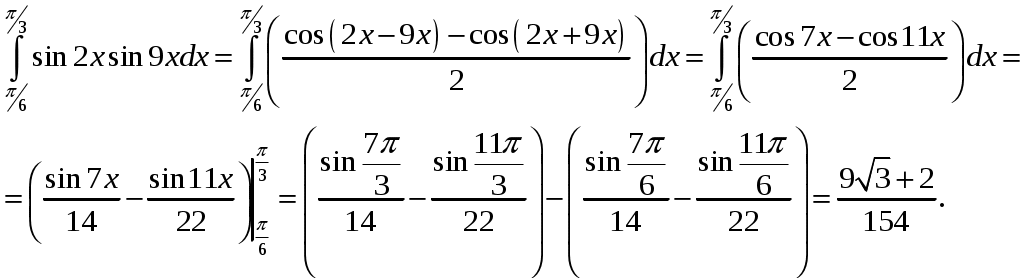 Ответ:  Вычислить несобственные интегралы или установить их расходимость 12.  ; Решение. Это несобственный интеграл I рода (с бесконечным пределом интегрирования). Согласно определению несобственного интеграла I рода 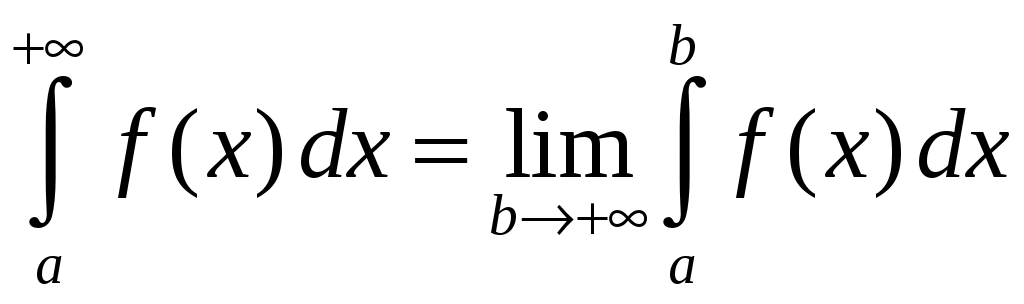 имеем 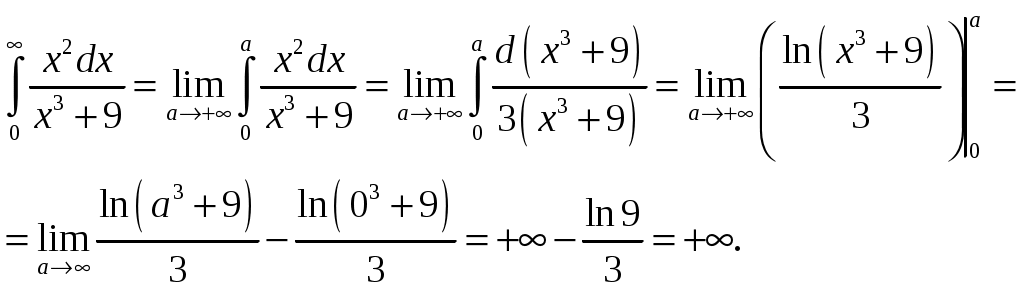 Ответ: интеграл расходится. 13.  .Решение. Это несобственный интеграл II рода. Согласно определению несобственного интеграла II рода 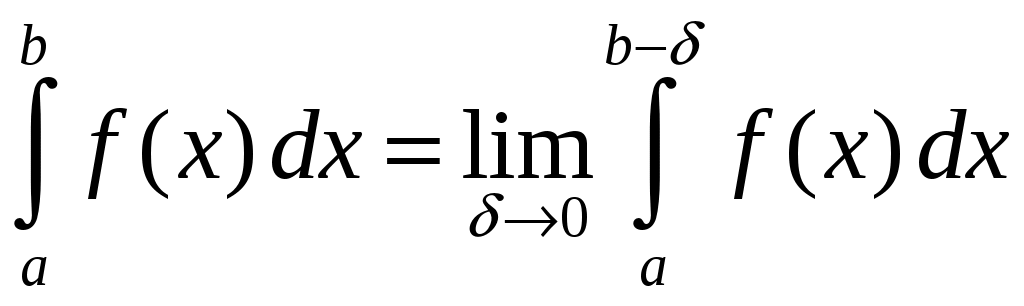 имеем 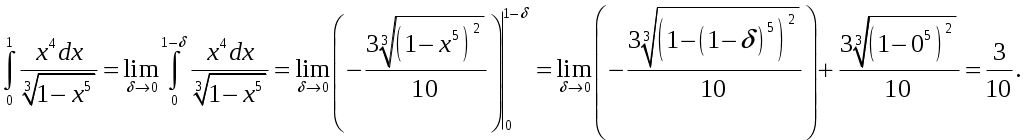 Данный интеграл сходится.Ответ: интеграл сходится. Выяснить сходимость несобственных интегралов 14. 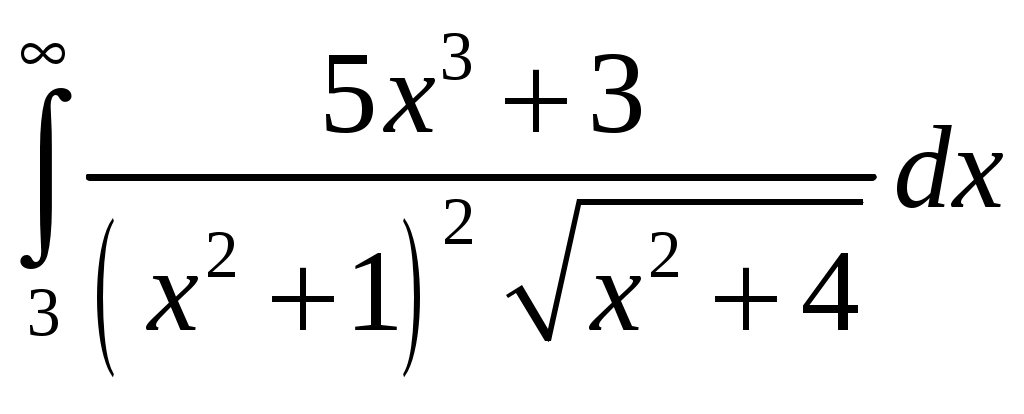 ; Так как при 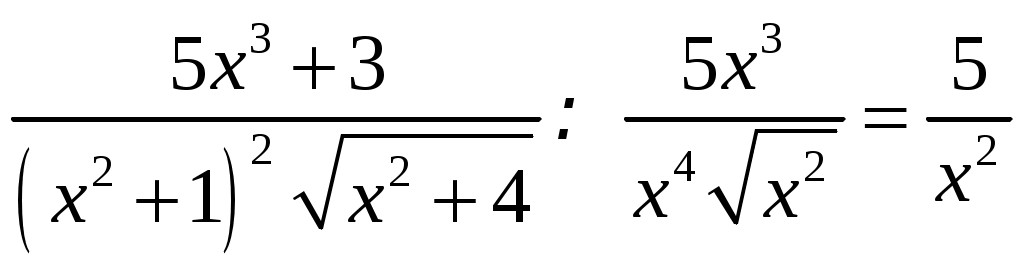 :  , то имеем сопоставление интегралов в виде частного и общего признаков сравнения: 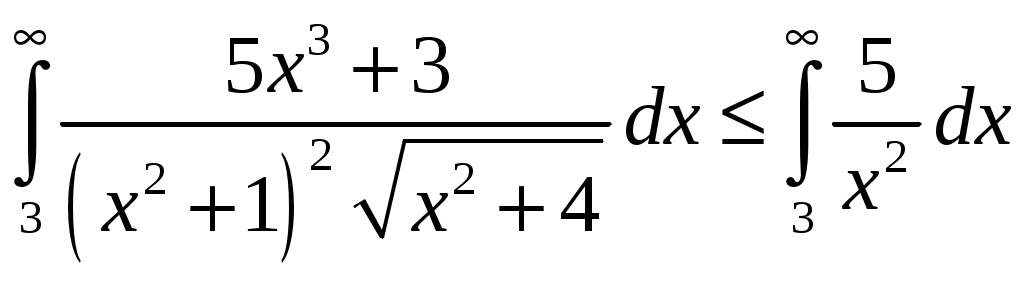 . .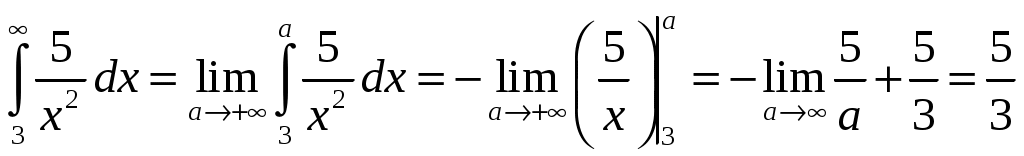Поскольку данный интеграл сходится, то исследуемый интеграл тоже сходится согласно общему признаку сравнения несобственных интегралов. Ответ: интеграл сходится. 15.  .Решение. Решение. Для интеграла 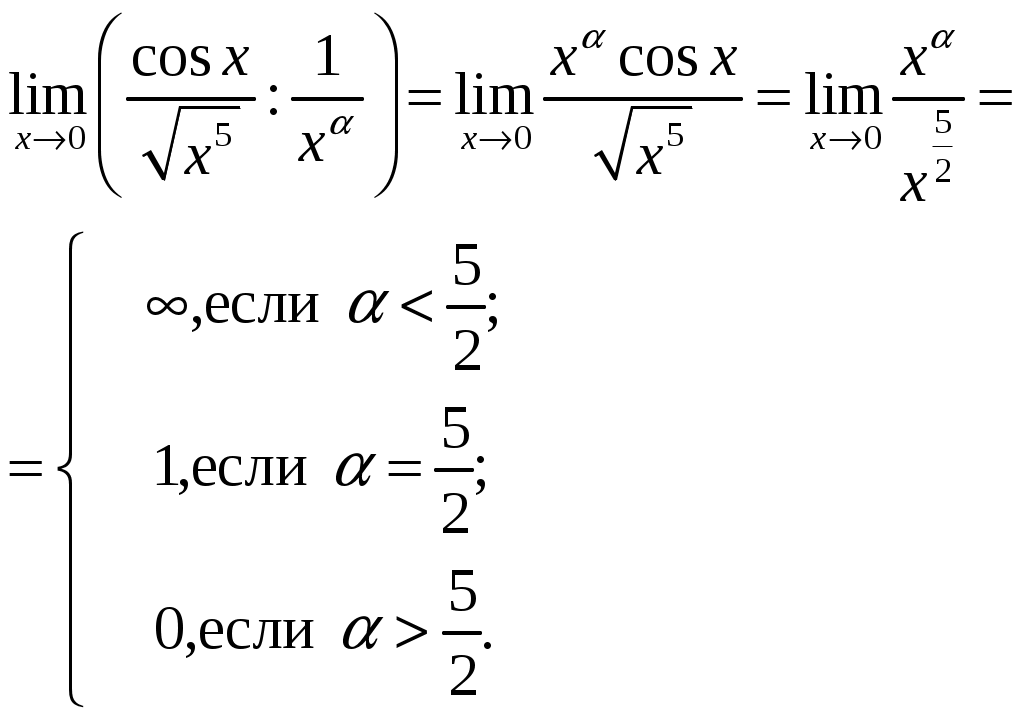подынтегральная функция имеет особенность в точке  . Находя порядок роста этой функции относительно  , имеем Таким образом, порядок роста равен  и интеграл расходится. Ответ: интеграл расходится. 16. Найти площадь области, ограниченной линиями  Решение. Координаты точек пересечения линий находим из системы: 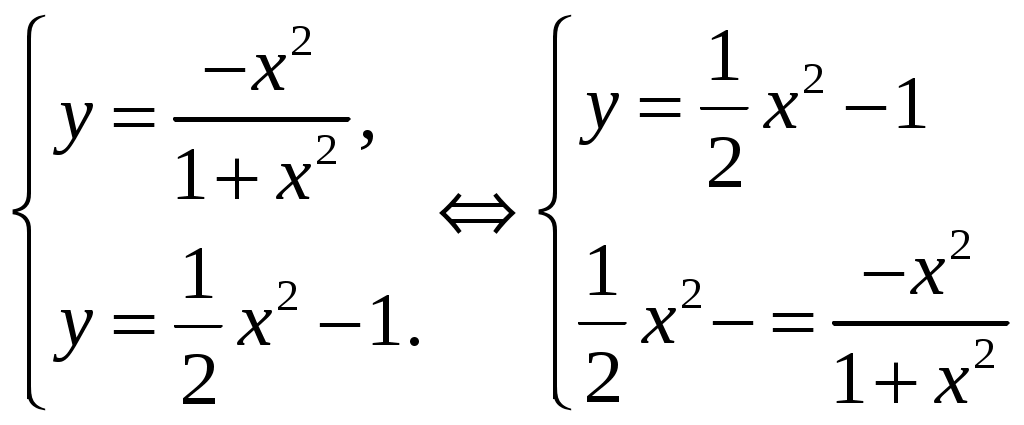 Отсюда:  и  .Строим заданные линии на плоскости ХOУ. Составляем определенный интеграл:  где 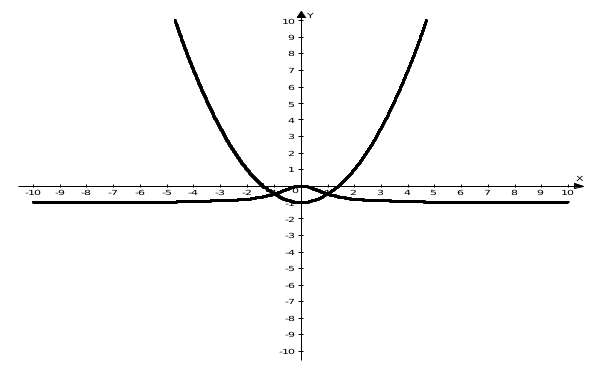 – линия, ограничивающая область сверху;  – линия, ограничивающая область снизу;  – наименьшее значение переменной x в области;  – наибольшее значение переменной x в области. Искомая площадь: 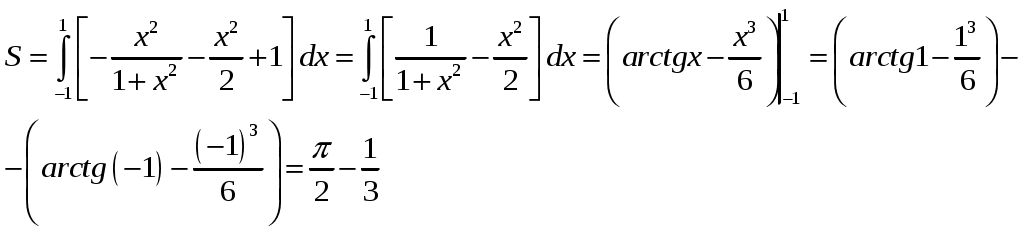 Ответ.  кв.ед.17. Найти длину дуги кривой, заданной в полярной системе координат уравнением  Решение. Длина дуги кривой заданной в полярных координатах находится по формуле: 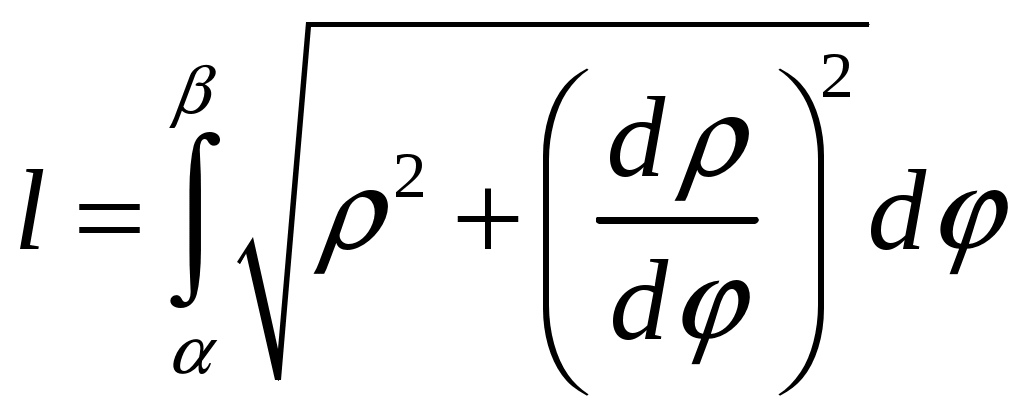 .Находим:  .Получаем: 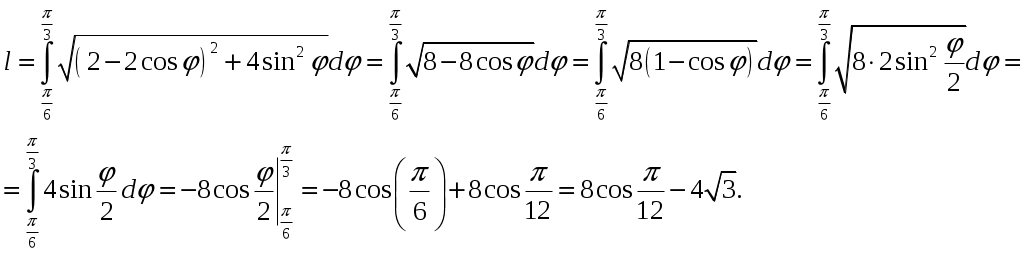 Ответ:  . |