Высшая математике. Контрольная работа 1 Элементы векторной алгебр и аналитической геометрии Задачи 110
 Скачать 340.5 Kb.
|
Контрольная работа №1Элементы векторной алгебр и аналитической геометрииЗадачи 1-10. Даны векторы a,b,c,d. Для указанных в пп. 1-3 векторов требуется: 1) вычислить скалярное произведение векторов из пункта; 2) найти модуль векторного произведения векторов; 3) проверить коллинеарность и ортогональность векторов; 4) убедиться, что векторы a,b,c образуют базис; 5) найти координаты вектора d в этом базисе. 9) a=3i+j+8k, b=j+3k, c=i+2j-k, d=2i-k; 1) 3a, -2c; 2) 3b, c; 3) a, b. Решение: 1)формула: ab=x1x2+y1y2+z1z2 3a=(9, 3, 24); -2c=(-2, -4,2); 3a*(-2c)=9(-2)+3(-4)+24*2=18  2)Формула: [a,b]= 3b=(0, 3, 9); c=(1, 2, -1);  [3b, c]= =-21i+9j-3k Модуль векторного произведения векторов: |[3b, c]|= (-21)2+92+(-3)2 = 23,04 3) Векторы a=3i+j+8k, b=j+3kне коллинеарные. ab=3*0+1*1+8*3=25, векторы а и b не ортагональны, потому что не равны 0.  4) abc= = =-3+3+0-8-18-0=-26 0, векторы a,b,c образуют базис. 5) Вектор d представим как: d=xa+yb+zc Это равенство равносильно равенствам: 2=3x+0y+1z; 0=1x+1y+2z; -1=8x+3y-1z Решив полученную систему уравнений, найдём x, y, z. x= , y= , z= d= a b + c, в данном базисе вектор d имеет координаты x= , y= , z= Задачи 11-20. Даны вершины A(x1, y1), B(x2, y2), C(x3, y3) треугольника ABC. Требуется найти: 1) уравнение стороны AB; 2) уравнение высоты CH и длину этой высоты; 3) уравнение медианы AM; 4) точку N пересечения медианы AM и CH; 5) уравнение прямой, параллельной стороне AB и проходящей через вершину C; 6) внутренний угол при вершине A и внешний угол при вершине C. 19. A(4,-4), B(8,2), C(3,8). Р  ешение:1)Уравнение прямой: = , = , 3x-2y-20- уравнение стороны AB. 2  )Сперва ищем перпендикулярность прямой 2x+3y+c=0, 2*3+3*8+c=0, c=-30, пришли к уравнение высоты: 2x+3y-30=0.Ищем длину высоты от точки С до прямой AB d=  d= 7,5 3)Ищем координаты точки М: Xм=Xb+Xc / 2 = 8+3 / 2 = 11 / 2 Yм=2+8 / 2 = 5 м(11/2, 5) Следовацельно y-(-4) / 5-(-4) = x-4 / 11/4-4, 3x-0,5y-14=0 уравнение медианы AM. 4) 2x+3y-30=0 => x=5,7; y=6,2; N(5,7; 6,2) 3x-0,5y-14=0 5) 3x-2y+c=0, 3*3-2*8+c=0, c=7; 3x-2y+7=0 -уравнение прямой, параллельной стороне AB и проходящей через вершину C. 6) Внутренний угол при вершине Aопределим как угол междупрямыми AB и AC, формула: tg ua= A1B2-A2B1 / A1A2+B1B2 Уравнение прямой АС: y-(-4) / 8-(-4) = x-4 / 3-4, 12x+y-44=0 От сюда: tg ua= 3*1-12*(-2) / 3*12-2*1 = 27 / 34 Тогда: ua = arctg (0,7941) 0,6771 rad, ua = 38,5o Уравнение прямой ВС: y-2 / 8-2 = x-8 / 3-8, 6x+5y-58=0 От сюда: tg uc = 12*5-6*1 / 12*6+1*5 = 54 / 77 Тогда: uc = arctg (0,7013) = 0,6116, uс = 35o Внешний угол при вершине Cсоставит uс’=360o-uс=360o-35=325o Задачи 21-30. Составить канонические уравнения 1) эллипса, 2) гиперболы, 3) параболы по известным из условий 1 – 3 параметрам. Через aи b обозначены большая и малая полуоси эллипса или гиперболы, через F – фокус кривой,  – эксцентриситет, 2 c– фокусное расстояние,  – уравнения асимптот гиперболы, D– директриса кривой, A, B– точки, лежащие на кривой. 29.  3) ось симметрии  и  .Решение: 1) Каноническое уравнение эллипса определяется: x2 / a2 + y2 / b2 = 1 (1) a - большая, b - малая полуочи. x1=-c, y1=0; x2=c, y2=0 f1(-c;0), f2(c, 0) c= a2-b2 (2) a=13, f(-5,0), c=5 из формулы (2) b= a2-c2 = 132-52 = 12, от сюда уравнение эллипса x2/132 + y2/122 = 1 2) Каноническое уравнение гиперболы определяется: x2 / a2 – y2 / b2 = 1 (3) a - действительная, b – мнимая полуоси. x1=-c, y1=0; x2=c, y2=0 f1(-c;0), f2(c, 0) c= a2+b2 (4) b=4, f(-7,0), c=7 из формулы (4) b= с2-b2 = 72-42= 33, от сюда уравнение гипербылы x2 / 33 - y2 / 16 = 1 3) Каноническое уравнение параболы определяется: y2=2px (5) Уравнение директрисы: x=-p / 2 (6) По условию директриса x=-3 / 8 из формулы (6) p=3 / 4, от сюда уравнение параболы y2=2*3/4 x y2=3/2 x Задачи 31-40. Даны четыре точки A1(x1,y1,z1), A2(x2,y2,z2), A3(x3,y3,z3), A4(x4,y4,z4). Требуется найти: 1) уравнение плоскости A1A2A3; 2) уравнение прямой, проходящей через точку A4, перпендикулярно плоскости A1A2A3; 3) расстояние от точки A4 до плоскости A1A2A3; 4) синус угла между прямой A1A4 и плоскостью A1A2A3; 5) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3. 39. A1(1,-2,7), A2(4,2,10), A3(2,3,5), A4(5,3,7). Решение: 1) Уравнение плоскости проходящей через три точки m1 (x1,y1,x1), m2 (x2,y2,x2), m3 (x3,y3,x3) имеет вид: x-x1 y-y1 z-z1 x-1 y+2 z-7 x2-x1 y2-y1 z2-z1 = 0 3 4 3 = 0 (x-1)(-23)-(y+2)(-9)+(z-7)11=0 x3-x1 y3-y1 z3-z1 1 5 -2 -23x+9y+11z-36=0 - уравнение плоскости A1A2A3. 2) Уравнение прямой, проходящей через точку A4, перпендикулярно плоскости A1A2A3 имеет нормальный вектор n=(-23,9,11). От сюда уравнение искомой прямой x=5-23t, y=3+9t, z=7+11t  3) , xo=5, yo=3, zo=7, A=-23, B=9, C=11, D=-36 d=|-23*5+9*3+11*7-36| / (-23)2+92+112 =183 / 731 = 6,8 4  ) Sin u= , составим уравнение прямой А1А4 проходящей через две точки:x-x1 / x2-x1=y-y1 / y2-y1=z-z1 / z2-z1 x-1 / 5-1 = y-(-2) / 3-(-2) = z-7 / 7-7 x-1 / 4 = y+2 / 5 = z-7 / 0 a1=4, a2=5, a3=0 Sin u= |-23*4+9*5+11*0| / (-23)2+92+112 * 42+52+02 = 731 / 29971 0,2715  5) Cos u = , для плоскости Оху: A1=0, B1=0, C1=1 для плоскости A1A2A3: A2=-23, A2=9, A3=11 Cos u = 0*(-23)+0*9+1*11 / (-23)2+92+112 * 02+02+12 = 11 / 731 0,4069 Контрольная работа №2 Элементы линейной алгебры Задачи 41-50. Даны две матрицы A и B. Требуется найти: 1)  ; 2) A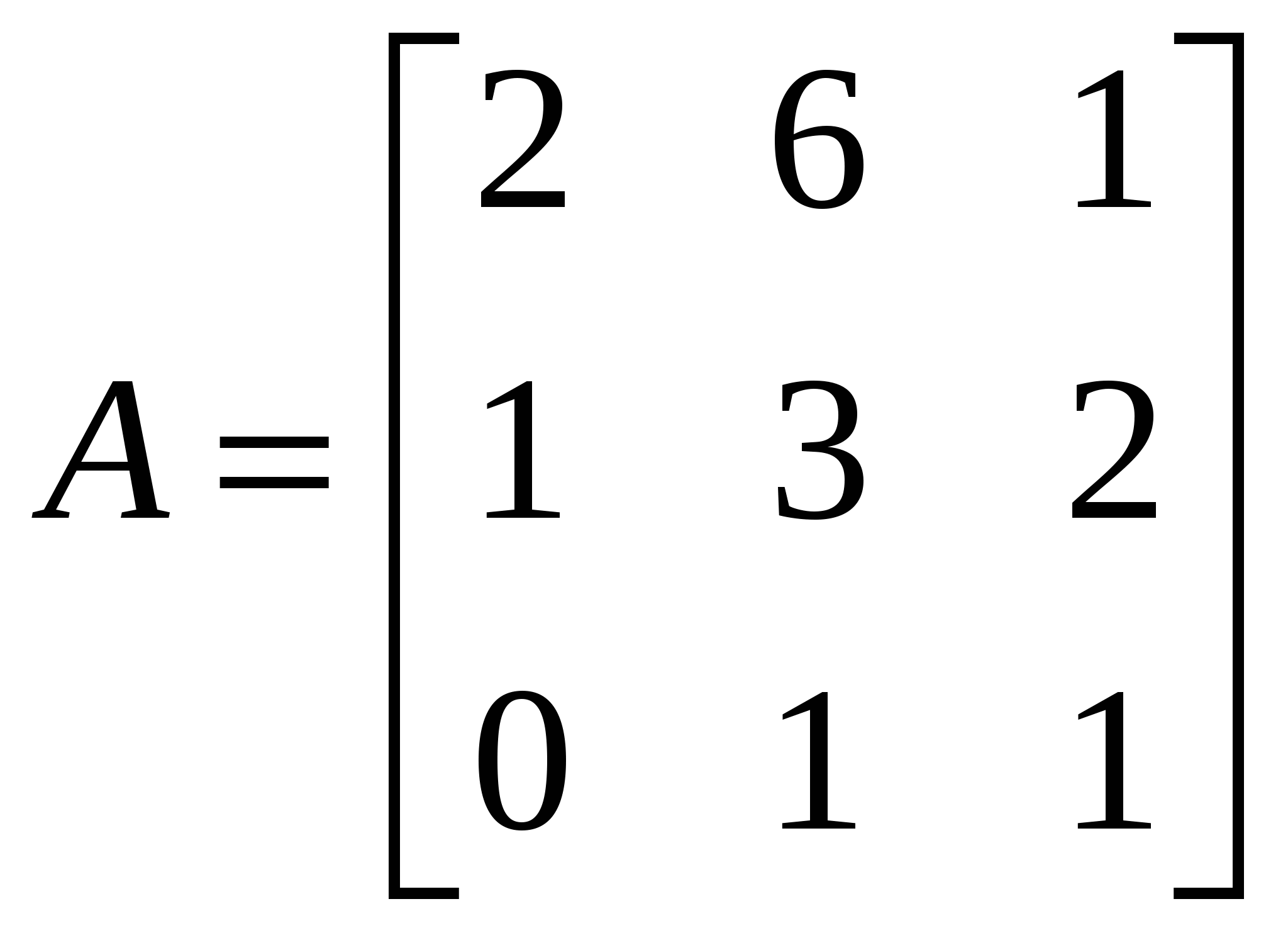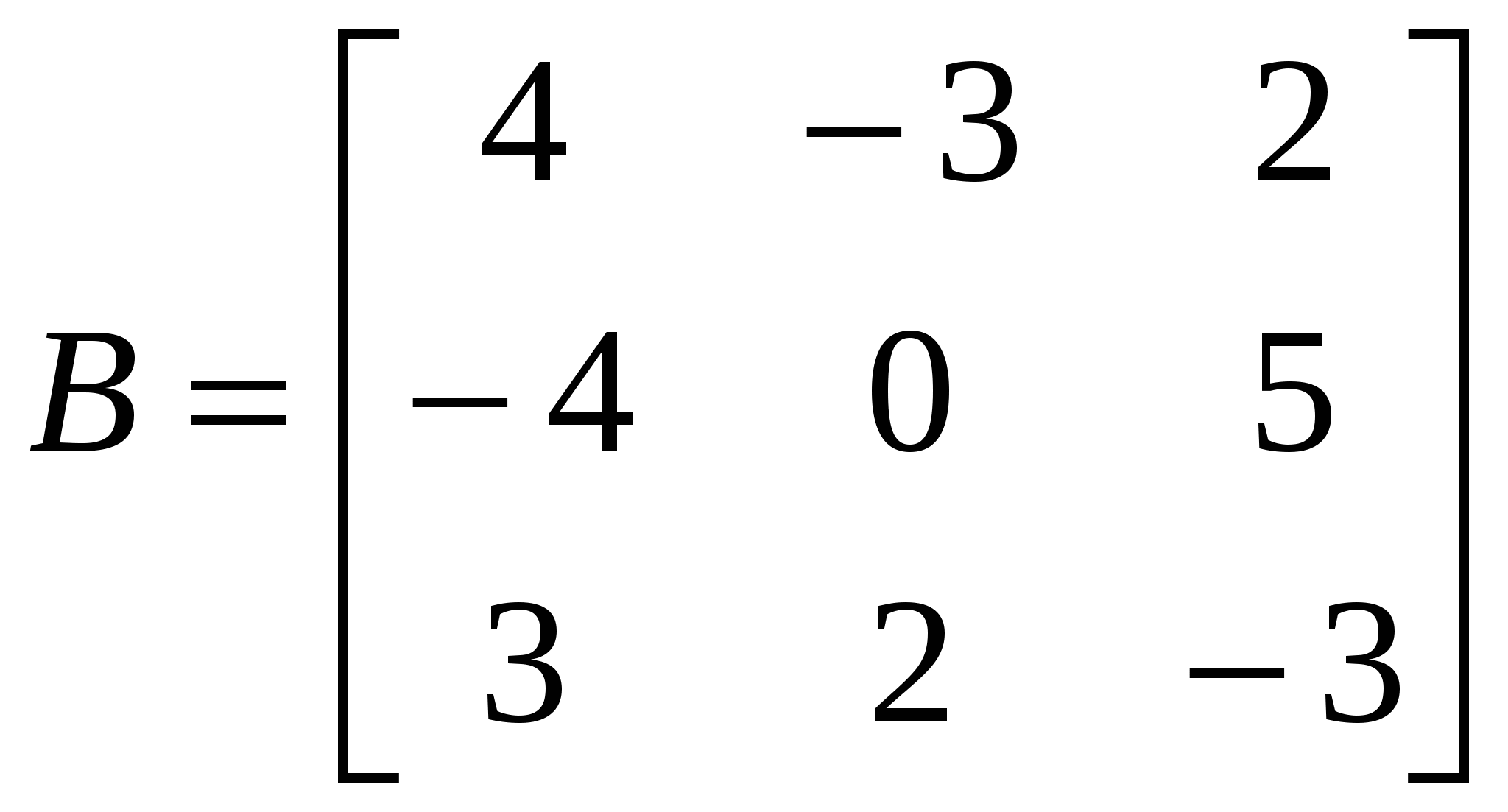-1; 3)  , где E - единичная матрица третьего порядка.49.  ,  .Решение: 2 6 1 2 6 1 4 -4 3 10 31 15 4 -4 3 14 27 18 1) A2+BT = 1 3 2 * 1 3 2 + -3 0 2 = 5 17 9 + -3 0 2 = 2 17 11 0 1 1 0 1 1 2 5 -3 1 4 3 2 5 -3 3 9 0 A11 A21 A31 2 6 1 2) Формула: A-1=1 / detA A12 A22 A32 detA = 1 3 2 = 6+1+0-0-4-6= -3 0 A13 A23 A33 0 1 1 A11=(-1)1+1 = 1 A21= - = -5 A31= = 9 A12=(-1)1+2 = -1 A22= = 2 A32= - = -3 A13=(-1)1+3 = 1 A23= - = -2 A33= = 0 1 -5 9 -1/3 5/3 -3 A-1=1 / -3 -1 2 -3 = 1/3 -2/3 1 1 -2 0 -1/3 2/3 0  1 0 0 4 -3 2 -1/3 5/3 -3 1 0 0 -3 10 -15 1 0 0 -4 10 -153) E= 0 1 0 = -4 0 5 * 1/3 -2/3 1 - 0 1 0 = -1/3 -10/3 12 - 0 1 0 = -1/3 -13/2 12 = 0 0 1 3 2 -3 -1/3 2/3 0 0 0 1 2/3 5/3 -7 0 0 1 2/3 5/3 -8 = -121 / 3 = -40,333 Задачи 51-60. Проверить, совместна ли система уравнений, и в случае совместности решить ее: 1) по формулам Крамера; 2) методом Гаусса; 3) с помощью обратной матрицы (матричным методом). 59. 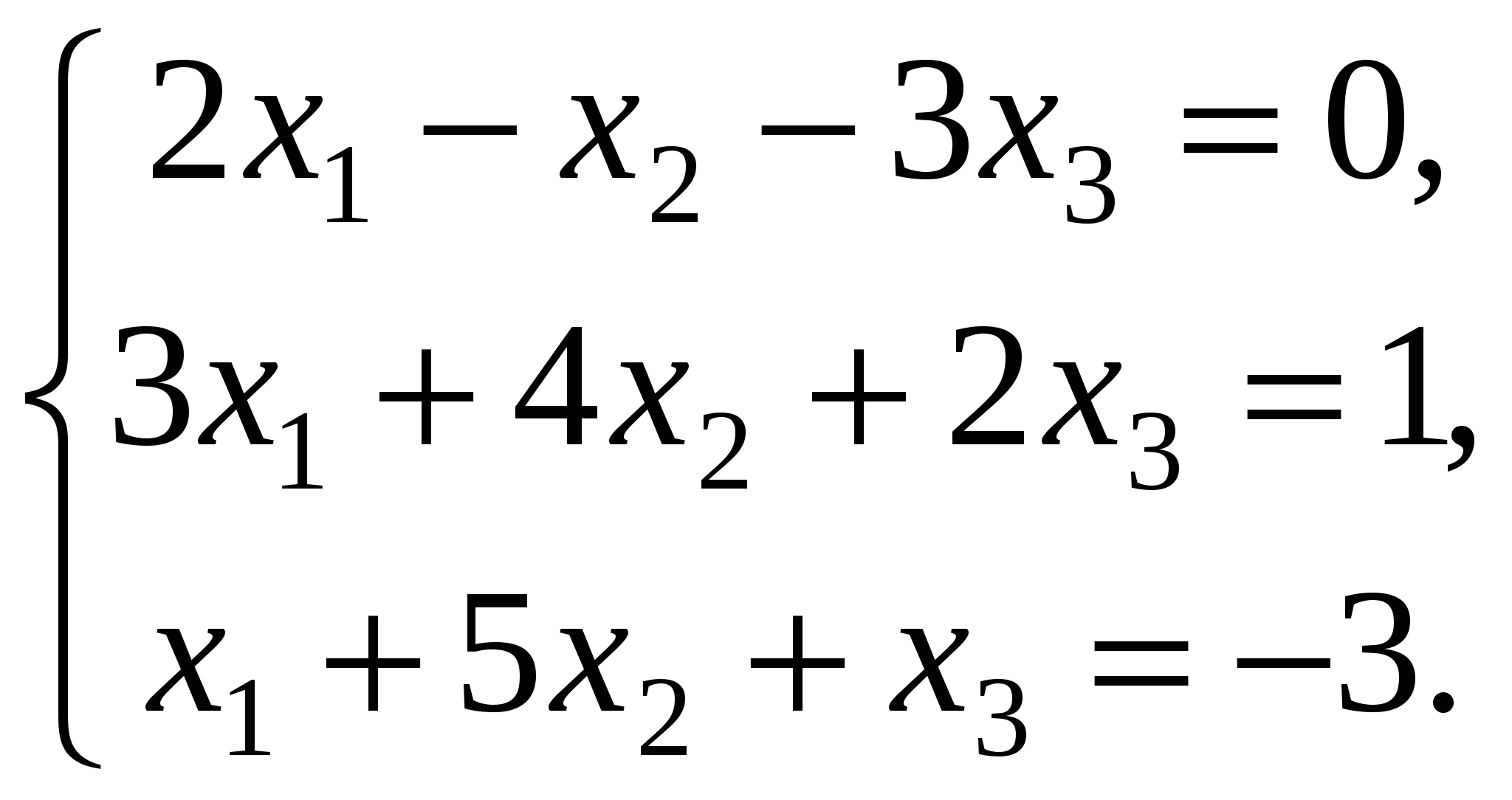 Решение: 0 -1 -3 1) Находим определители: ∆1= 1 4 2 = 0-15+6-36-0+1=-44 -3 5 1 2 0 -3 ∆2= 3 1 2 = 2+27+0+3+12-0=44 1 -3 1 2 -1 0 ∆3= 3 4 1 = -24+0-1-0-10-9=-44 1 5 -3 По формуле Крамера находим: x1=∆1 / ∆= -44 / -44 = 1, x2 = 44 / -44 = -1, x3 = -44 / -44 = 1 2 -1 -3 0 2 -1 -3 0 2 -1 -3 0 2) Преобразуем расширенную матрицу: 3 4 2 1 > 0 -11 -13 -2 > 0 -11 -13 -2 1 5 1 -3 0 -11 -5 6 0 0 -8 -8 3яя матрица соответствует системе уравнения: 2x1-x2-3x3=0 -11x2-13x3=-2 x1= 1, x2= -1, x3= 1 -8x3=-8 2 -1 -3 x1 0 3)ax=b, a= 3 4 2 , x= x2 , b= 1 x=a-1*b, найдём обратную матрицу а-1 1 5 1 x3 -3 A11= = -6 A21= - = -14 A31= = 10 A12= - = -1 A22= = 5 A32= - = -13 A13= - = 11 A23= - = -11 A33= = 11 -6 -14 10 -6 -14 10 0 0 -14 - 30 -44 1 A-1=1/-44 -1 5 -13 , от сюда x=1 / -44 -1 5 -13 * 1 = 1 / -44 0 + 5 - 39 = 1 / -44 44 = -1 11 -11 11 11 -11 11 -3 0 -11 - 33 -44 1 x1=1, x2=-1, x3=1 Задачи61-70. Найти собственные значения и собственные векторы матрицы A. 69. 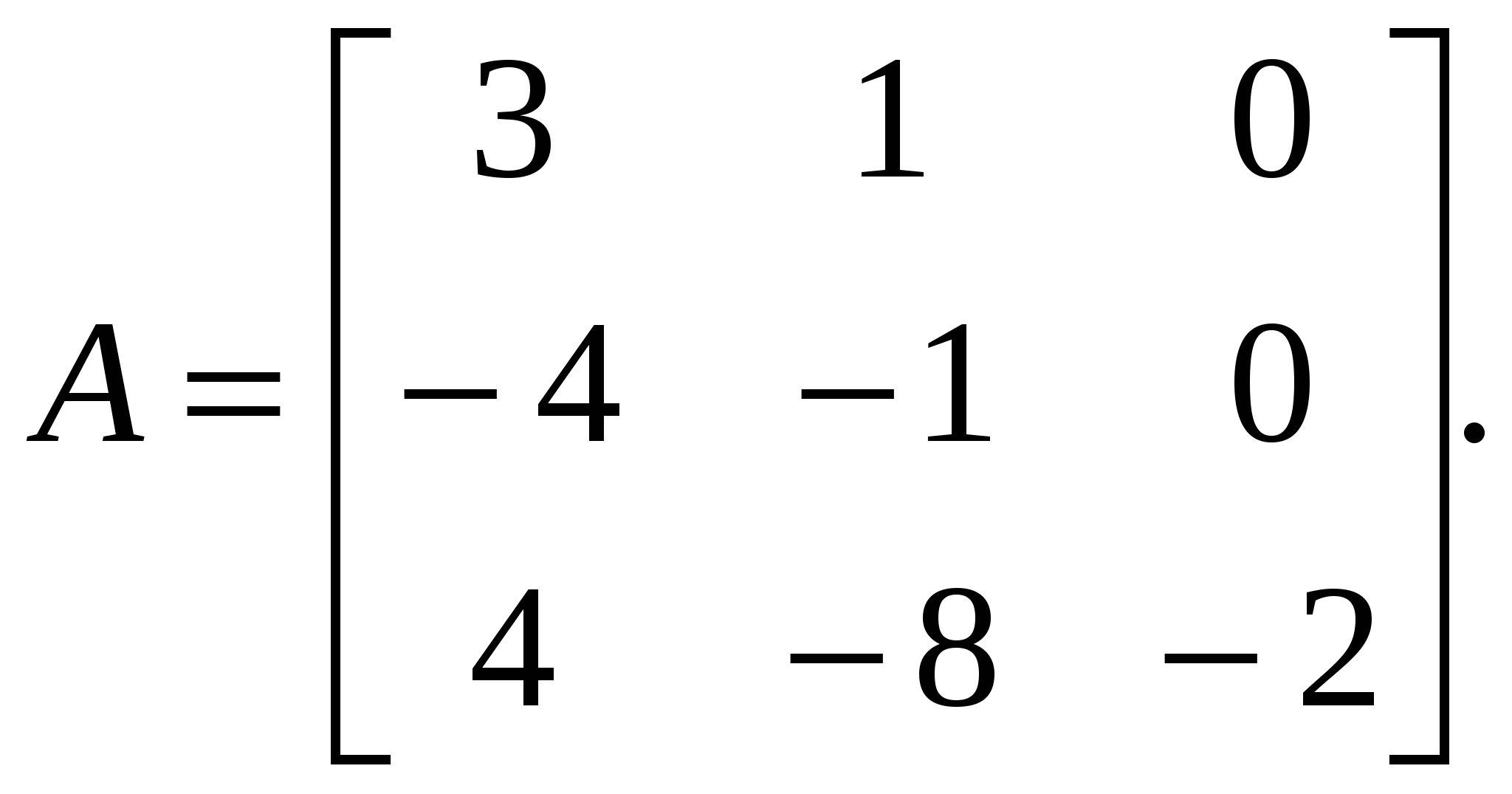 Решение: Составляем характеристическое уравнение матрицы. 3-ℓ 1 0 A= -4 -1-ℓ 0 = 0 4 -8 -2-ℓ (-2-ℓ)((3-ℓ)(-1-ℓ)+4)=0 (-2-ℓ)(ℓ2-2ℓ+1)=0 ℓ1=-2, ℓ2=1, ℓ3=1 Линейное преобразование с данной матрицей имеет два действительных собственных значения ℓ1=-2, ℓ2=1. Для того чтобы найти соответствующий собственный вектор, используем систему уравнений: (3-ℓ)x1+x2 = 0 -4x1+(-1-ℓ)x2 = 0 (1) 4x1-8x2+(-2-ℓ)x3 = 0 При ℓ=-2 система уравнений (1) принимает вид: 5x1+x2 = 0 -4x1+x2 = 0 4x1-8x2 = 0 x1=0, x2=0, получив x3=-1, получим вектор x=(0, 0, -2). При ℓ=1 система уравнений (1) принимает вид: 2x1+x2 = 0 -4x1+2x2 = 0 4x1-8x2-3x3 = 0 x1=-3/20x3, x2=3/10x3, получив x3=1, получили собственный вектор x=(- 3/20, 3/10, 1). Задачи 71-80.Используя теорию квадратичных форм, привести уравнение кривой второго порядка к каноническому виду и построить эту кривую. 79.  Решение: Уравнение второй степени: a11x2+2a12xy+a22y2+a13x+a23y+a33 (1) a11= 0, a12= 2, a13= 0 Первые 3 члена левой части уравнения (1) образуют квадратичную форму двух переменных x1=x, x2=y: f(x,y)= a11x2+2a12xy+a22y2= 4xy С  матрицей: А= Уравнение матрицы 0-ℓ 2 =0 ℓ2=42 0-ℓ Имеет корни ℓ1=-2, ℓ2=2, которые являются собственными значениями матрицы А. Найдём собственные векторы координаты которых (s,t) определяются из системы уравнений: -ℓs+2t=0 2s-ℓt=0 При ℓ1=-2, ℓ2=2 имеет две системы: 2s+2t=0 -2s+2t=0 2s+2t=0 2s-2t=0 И  з этих систем находим собственные векторы: u=(t,-t), v=(t,t), t 0. Если t=1, тогда u=(1,-1), v=(1,1). Из этого соствим матрицу В: В= С помощью матрицы В записываем ортогональное преобразование: x= x’+ y’= (x’+y’) y= x’+ y’= (-x’+y’) Это преобразование приводит данное уравнение кривой к каноническому виду: u(x’,y’)=4* (x’+y’)(-x’+y’)+4* (x’+y’)-4* (-x’+y’)-2=(x’+ )2-y’2-1=0 (x’- )2-y’2=1 уравнение определяющее гипербулу с действительной осью О1 Х, с центром в точке О1( ,0) и полуосями a и b. a=1,b=1 Построим данную кривую: 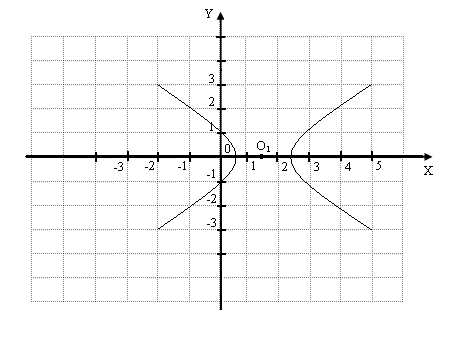 Контрольная работа №3Введение в математический анализЗадачи 81-90. Требуется: 1) выполнить действия над комплексными числами, записав результат в показательной форме; 2) найти все корни уравнения. 89. 1) 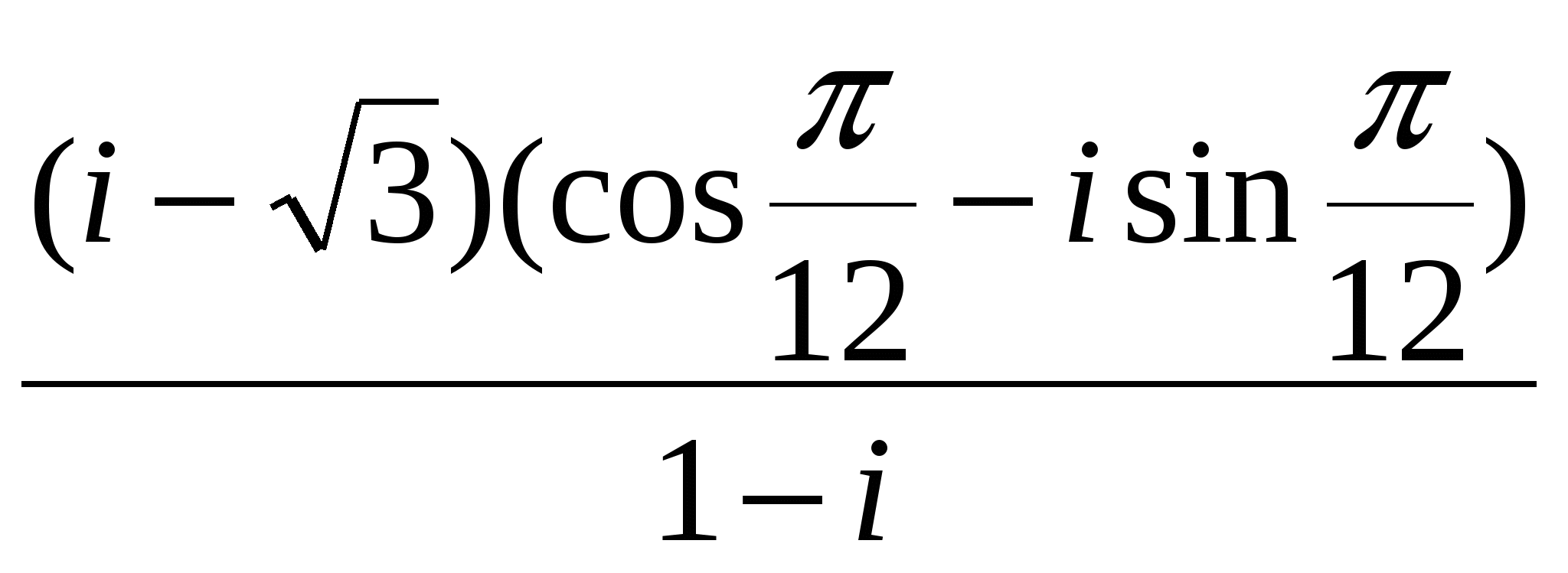 ; 2)  .Решение: 1) Представим два комплексных числа в тригонометрической форме (- 3 +i) и (1-i). Для первого числа: r1= (- 3 )2+12 = 2 Cos u1=- 3 / 2, Sin u1=1 / 2 => u=5п / 6 (- 3 +i)=2(Cos 5п/6 + i Sin 5п/6) Для второго числа: r2= 12+(-1)2= 2 Cos u2=1 / 2 = 2 / 2, Sin u2 = -1 / 2 = - 2 / 2 => u1= - п / 4 1-i= 2 (Cos(- п / 4)+i Sin(- п / 4)) Если z1=r1(Cosu1+i Sin u1) z2=r2(Cos u2+i Sin u2) z1z2=r1r2(Cos(u1+u2)+i Sin(u1+u2)) z1 / z2=r1 / r2 (Cos (u1-u2)+i(Sin(u1-u2)) ) (- 3 + i)(Cos п/12-i Sin п/12) = 2(Cos 5п/6+i Sin 5п/6)(Cos(-п/12)+i Sin(-п/12)) = 2(Cos(5п/6 – п/12)+i Sin(5п/6- -п/12)) = 2(Cos 3п/4+i Sin 3п/4) (- 3 + i)(Cos п/12 - i Sin п/12) / (1-i) = 2(Cos 3п/4+i Sin 3п/4) / 2 (Cos(-п/4)+i Sin(-п/4)) = 2 / 2 (Cos(3п/4- -(-п/4))+i Sin(3п/4-(-п/4)) ) = 2(Cos п+i Sin п) = - 2 r= 2 , Cos u = -1, Sin u=0 => u=п - 2 = 2 ei п 2) Основа формулы z3+pz+q=0, по ней расчітаем формулу z=u+v, где u=q2 / 4 + p3 / 27; v=q2 / 4 + p3 / 27 Составим вырожение q2/4 + p3/27 = (-9)2/4 + (-6)3 / 27 = 81 / 4 – 8 = 49 / 4 Находим u и v:   u1= v1=Следовательно u1=2, v1=1, равенство 3uv+p=0 выполняется по формулам: z1=u1+v1, z2=u1e+v1e2, z3=u1e2+v1e учитывая, что e=-1/2+i 3 / 2, e2=-1/2-i 3 / 2 находим z1=2+1=3 z2=2(-1/2+i 3 / 2)+1(-1/2-i 3 / 2)=-3/2+i 3 / 2 z3=2(-1/2 -i 3 / 2)+1(-1/2+i 3 / 2)=-3/2-i 3 / 2 Задачи 91-100. Построить график функции y=F(x), используя преобразования графика известной функции f(x). 99. F(x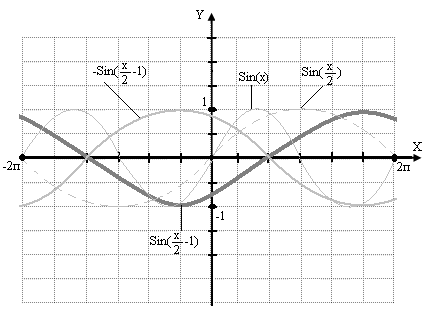)=  , f(x)= . Р  ешение:Построим график функций f(x)=Sin x. График функций f(x)=Sin( ) получим из графика функций f(x)-Sin x путём его растягивания вдоль оси 0x в два раза. График функций f(x)=Sin( -1)=Sin( ) получим использую график функций f(x)=Sin( ) путём его смещения вдоль оси Ох на 2 единицы вправо. Наконец график функций F(x)=-Sin( - 1) получим используя график f(x)=Sin( -1), принимая во внимание то, что они симметричны относительно оси Ох. Задачи 101-110. Вычислить пределы функций, не пользуясь правилом Лопиталя. 109. 1)  ; 2)  ; 3)  ; 4)  ; 5)  ; 6)  .Р  ешение:1) = (-6)2+2(-6)-24 / 2(-6)3+15(-6)+18 = 0 / -504 = 0 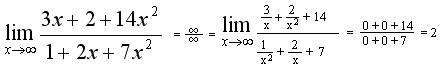 2) 3)   4) 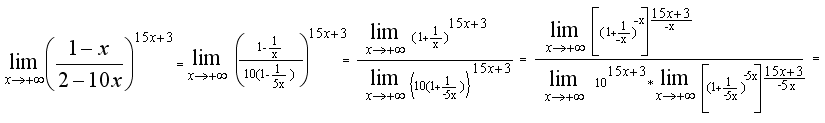 5) 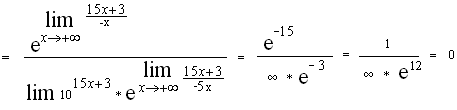 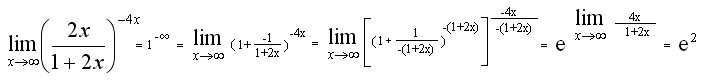 6) Задачи 111-120. Исследовать функцию f(x) на непрерывность и построить ее график. 119. f(x)= 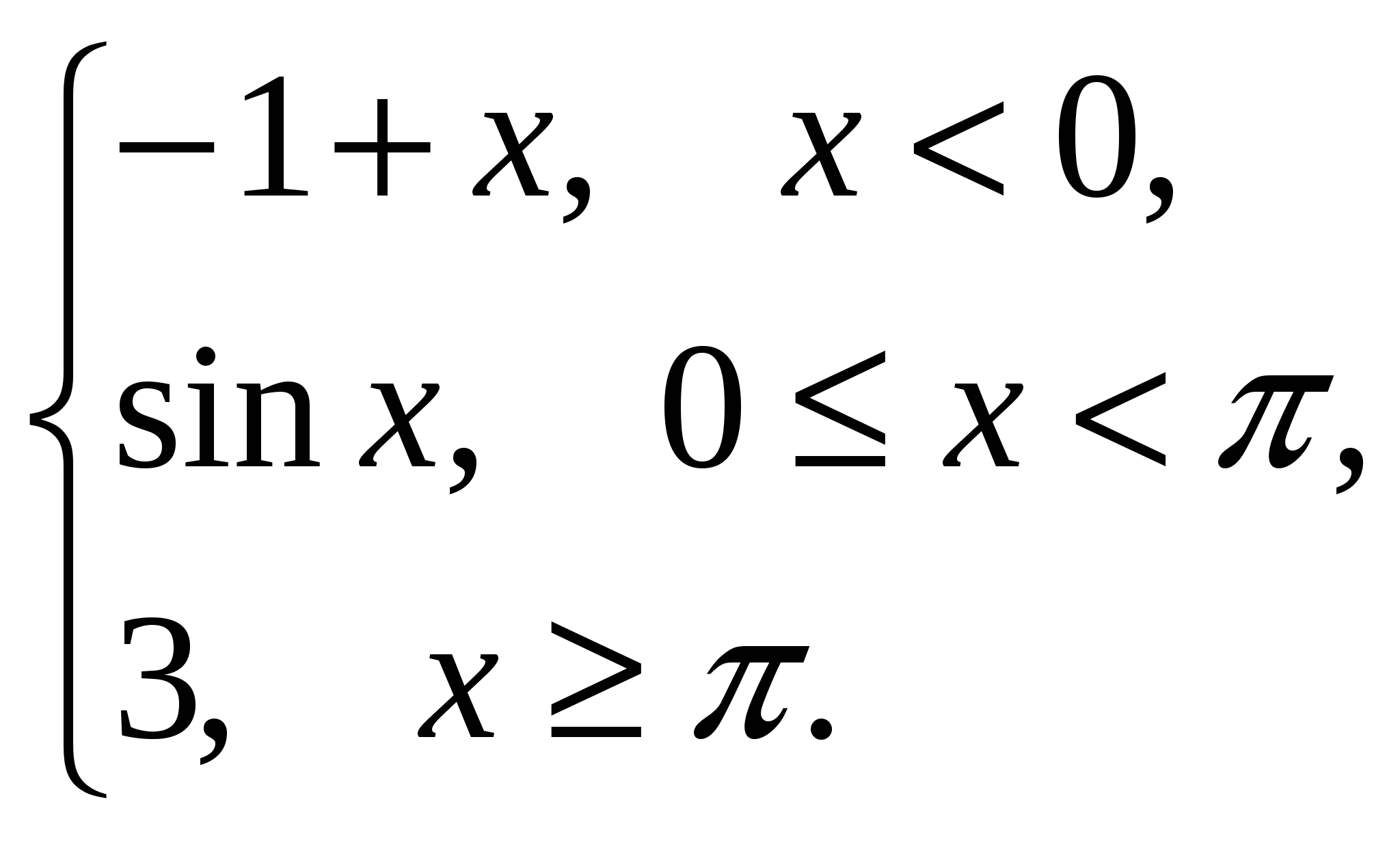 Решение: Поскольку f(x) задана тремя непрерывными элементарными функциями, то точками разрыва данной функции могут быть лишь точки x1=0 и x2=п. Проверим в этих точках выполнение условий. 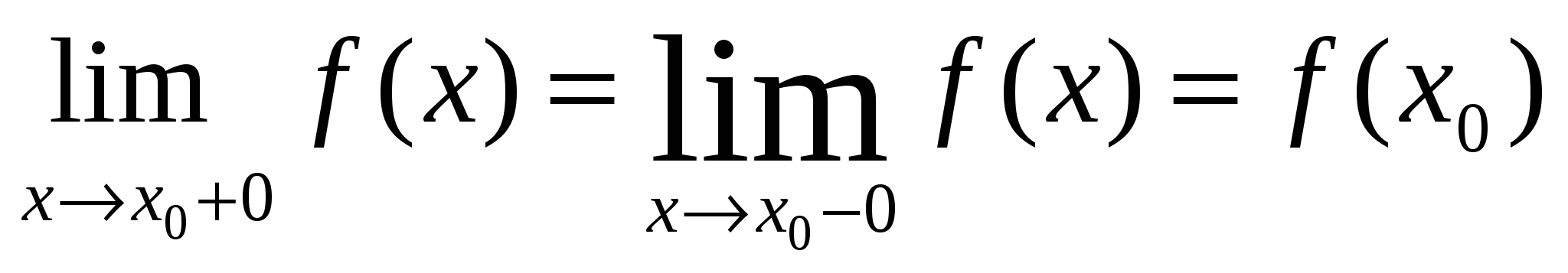 1)   Итак, в точке x1=0  , следовательно, точка x1=0 – это точка разрыва функции f(x). Поскольку односторонние пределы в этой точке конечны, то это точка разрыва первого рода. 2)  Итак, в точке x2=п  , следовательно, точка x2=п – это точка разрыва первого рода функции f(x).Построим график функций. 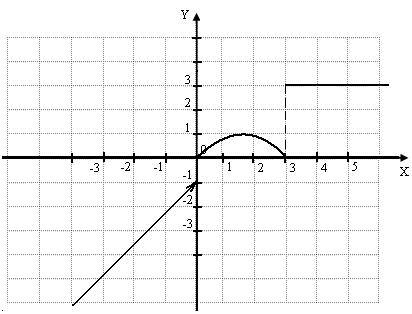 Литература.
|