Контрольная работа. Контрольная работа 1 Элементы векторной алгебры, аналитической геометрии и линейной алгебры
 Скачать 457.86 Kb. Скачать 457.86 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА № 1 Элементы векторной алгебры, аналитической геометрии и линейной алгебры 1.5. Найти объем параллелепипеда, построенного на векторах: 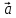 (−5; 0; 2); (−5; 0; 2); 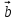 (8; 1; 3); (8; 1; 3); 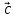 (1; −1; −2). Сделать чертеж. (1; −1; −2). Сделать чертеж.Объем параллелепипеда, построенного на векторах 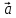 (X1;Y1;Z1), (X1;Y1;Z1), 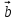 (X2;Y2;Z2), (X2;Y2;Z2), 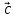 (X3;Y3;Z3) равен: (X3;Y3;Z3) равен: здесь X,Y,Z координаты вектора.  Где (-23) нашли как определить матрицы.  = -5 = -5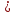 (1 (1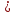 (-2) – (-1) (-2) – (-1)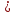 3) – 8 3) – 8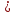 (0 (0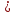 (-2) – (-1) (-2) – (-1)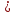 2) + 1 2) + 1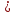 (0 (0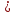 3-1 3-1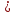 2) = -23 2) = -23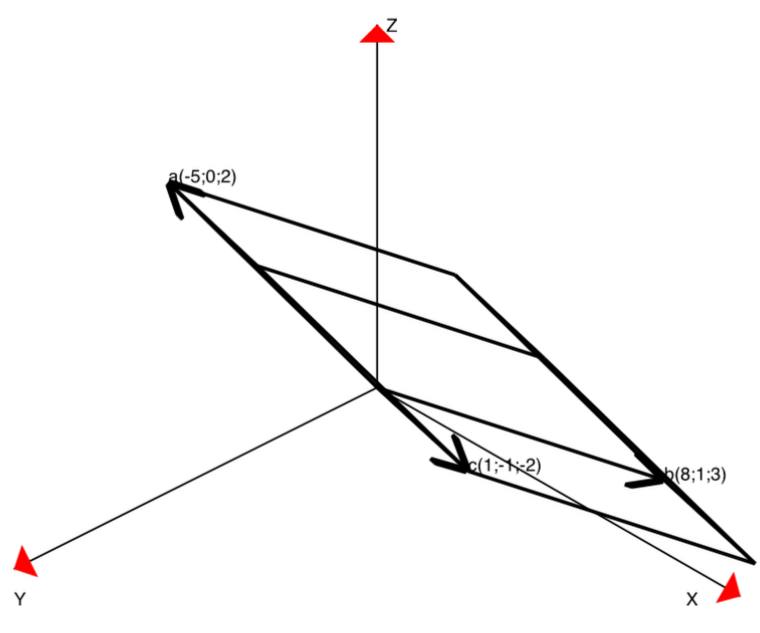 2.5. Даны вершины А(3; –2), В(4;–1), С(1; 3) трапеции ABCD(AD || BC).Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж. 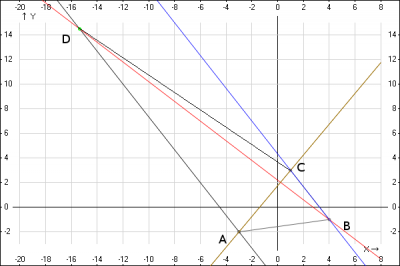 1.Найдем уравнение прямой AD. Даны координаты вершины A(3; -2) и сказано, что прямая AD || BC. Уравнение прямой AD будем искать, используя уравнение прямой проходящей через заданную точку в заданном направлении у - y0=k(x−x0) (1) Угловые коэффициент прямых kAD=kBC, как угловые коэффициенты двух параллельных прямых. Найдем_уравнение_прямой_BC.'>Найдем уравнение прямой BC. Известны координаты двух точек этой прямой В(4; -1), С(1; 3), поэтому уравнения прямой BC будем искать как уравнение прямой, проходящей через две заданные точки 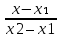 = = 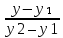 (2) (2)Подставляем координаты вершин: BC: 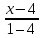 = = 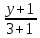 = =  y = y = 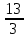 - - 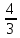 x xИз уравнения прямой получаем угловой коэффициент KBC= 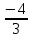 = =  kAD= kAD= 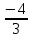 Найдем уравнение прямой AD, подставим координаты вершину A(-3; -2) и угловой коэффициент kAD= - 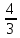 в уравнение (1) в уравнение (1) AD: y + 2 = - 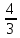 (x−3) = > y = −6 - (x−3) = > y = −6 - 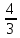 x x2. Найдем уравнение прямой BD. Даны координаты вершины В(4;-1) и сказано, что прямая BD ⊥ AC. Уравнение прямой BD будем искать, используя уравнение прямой проходящей через заданную точку в заданном направлении y − y0=k(x−x0) (1) AC: 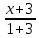 = = 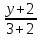 = =  y = y = 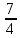 + +  x; x;kAC =  = =  kBD = kBD = 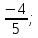 BD: y + 1 = - 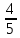 (x−4) = >y = (x−4) = >y = 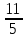 - - 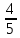 x ; x ;3. Найдем точку пересечения двух прямых AD и BD. 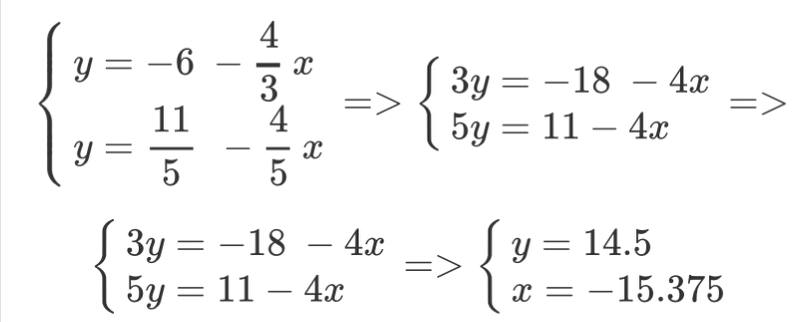 Ответ: координаты вершины D (-15.375; 14.5) 3.5. Решить систему линейных уравнений по правилу Крамера и методом Гаусса. Сделать проверку. 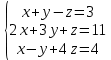 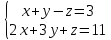 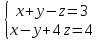  x = 2 y = 2 2+2-z=3 z=1 (x,y,z) = (2, 2, 1) 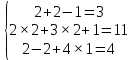 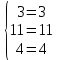 Решение: (x,y,z) = (2,2,1). Введение в математический анализ. Производная и ее приложения. 4.5. Найти пределы функций, не пользуясь правилом Лопиталя. a) 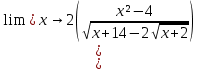 ; ;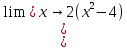 ; ; 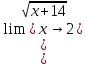 + 2 + 2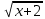 ); );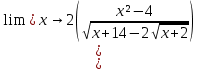 ; ;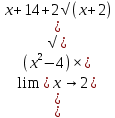 ; ;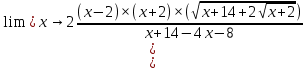 ; ;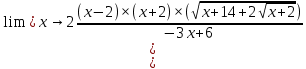 ; ;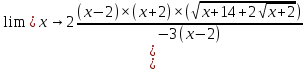 ; ;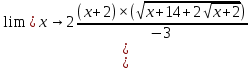 ; ;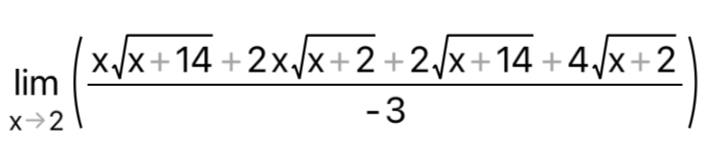 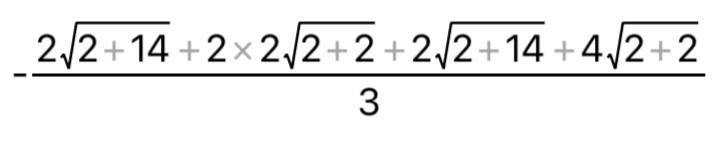 Решение: - 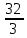  -10 -10 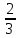 , -10.6 , -10.6б) 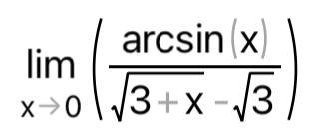 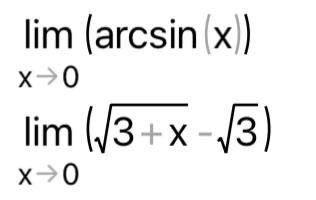 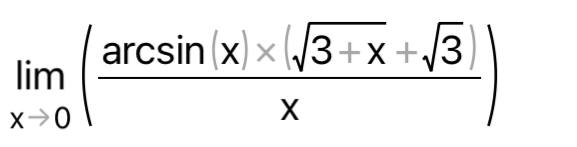 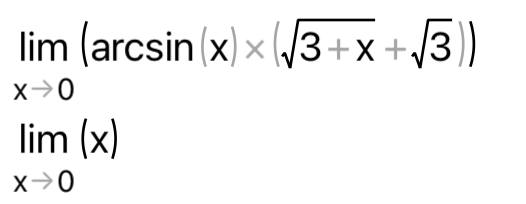 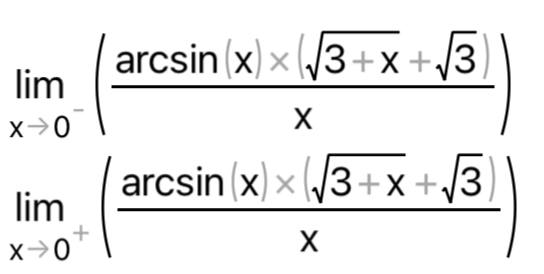 2 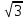 Решение: 2 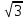  3,4641 3,4641В) 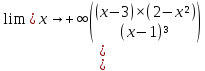 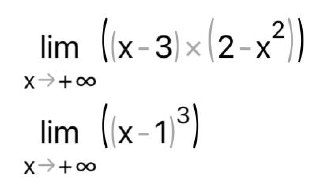 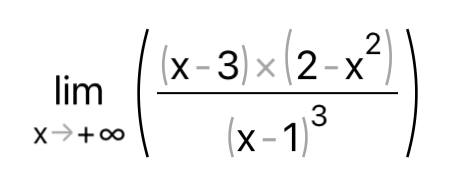 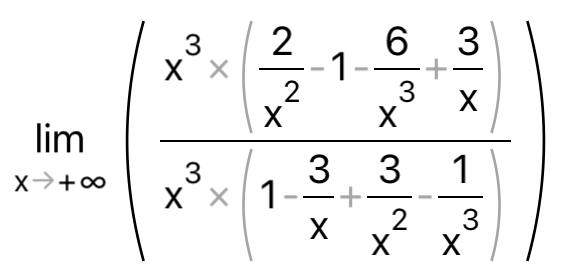  Решение: -1 Г)  ( (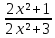 )x²-1 )x²-1 Решение:  5.5. Задана функция у=f(х). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж. 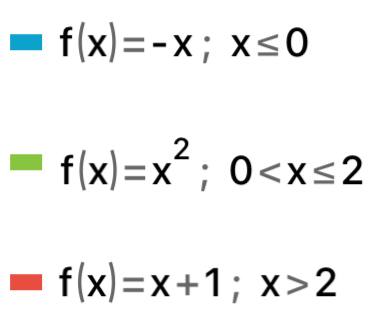 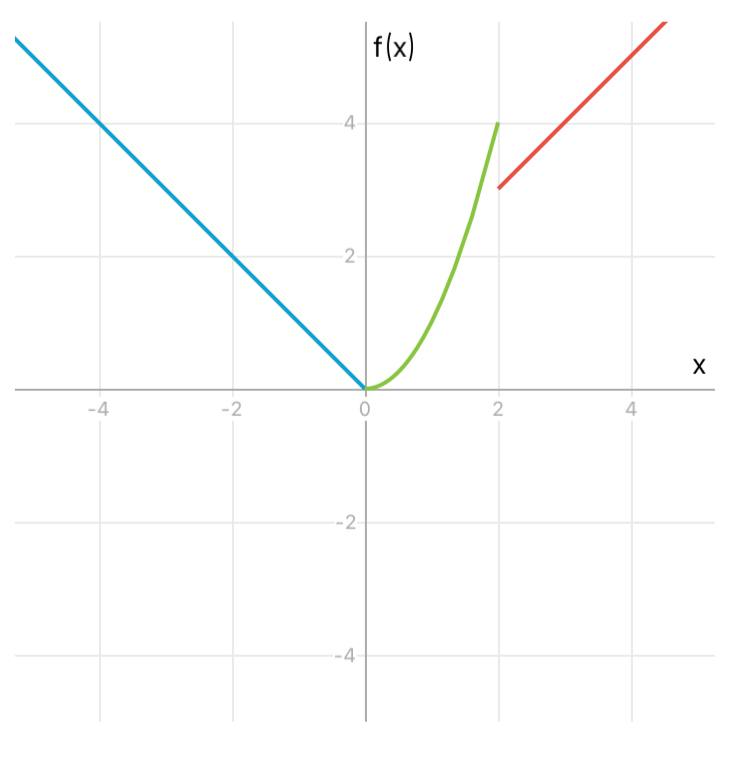 6.5. Методами дифференциального исчисления: а) исследовать функцию y = f (x) и по результатам исследования построить ее график; y = 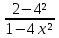 y´= 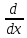 ( (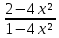 ) )y´= 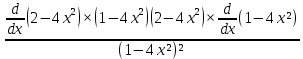 y´= 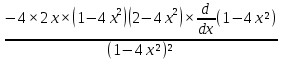 Решение: y´= 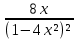 б) Найти наименьшее и наибольшее значения заданной функции на отрезке [1; 4]. f i0(x*) = 0 fI0(x*) = 0 fii0(x*)  0 fII0(x*) 0 fII0(x*)  0 0y´= - 8·x -8·x=0 x1=0 f(0)=-14 f(1)=-18 f(4)=-78 ответ: fmin=-78; fmax=-18 7.5. .Найти производные  данных функций. данных функций.а) y= 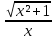 + arccos ( + arccos (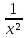 ) )y= 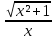 + + 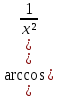 y= 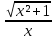 + + 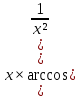 y= 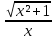 + + 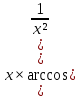 Решение: y = 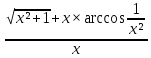 б) y = (x-1)exp(x2) Решение: y = xe(x2)-e(x2) в) x = t - ln sint, y = t + ln cost 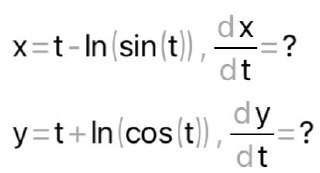 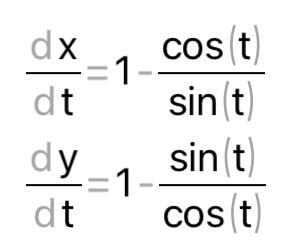 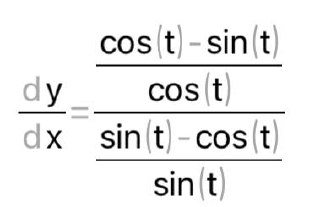 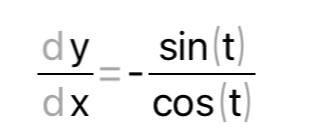 Решение: 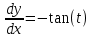 8.5. Найти неопределенные интегралы. Результаты проверить дифференцированием. 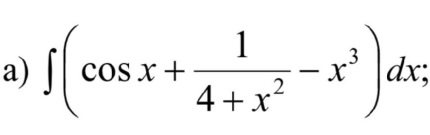 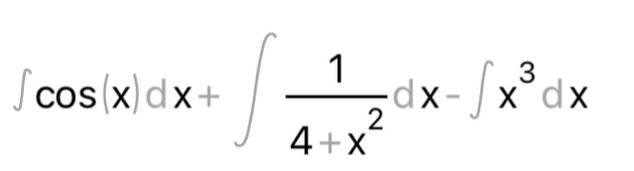 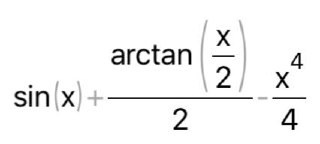 Решение: 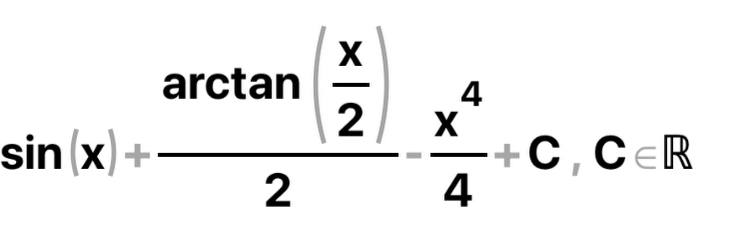 б) 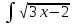 dx dx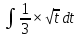 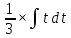  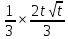 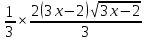 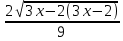 Решение: 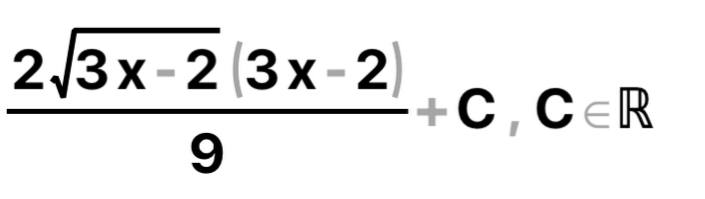 в) 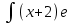 xdx xdxu = x+2 dv = exdx du = dx v = ex (x+2)ex - 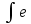 x dx x dx(x+2)ex - ex xex + ex Решение: xex+ex+c, C  R Rг) 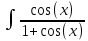 dx dx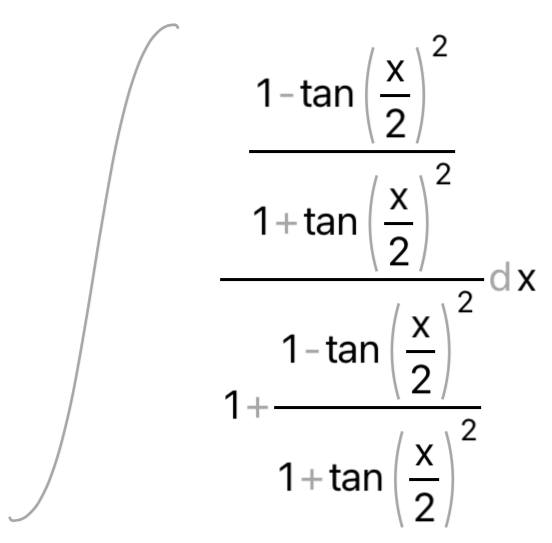 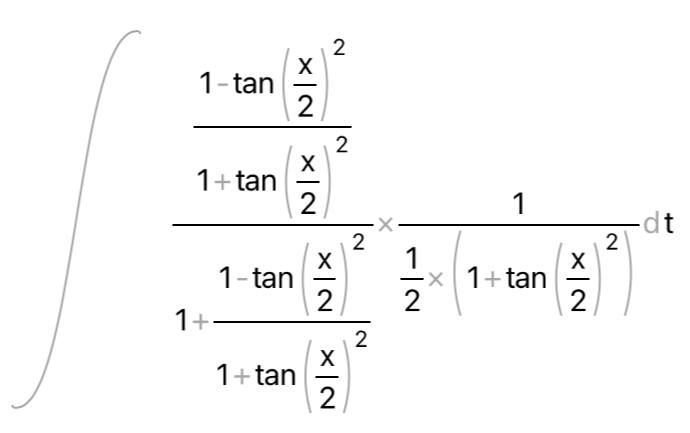 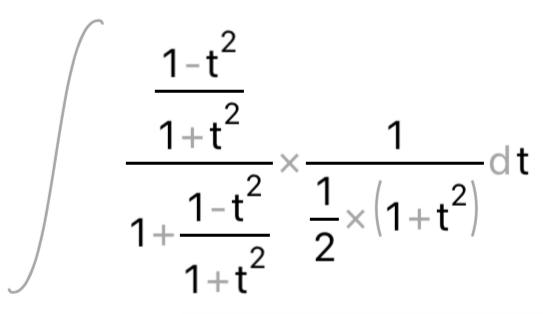 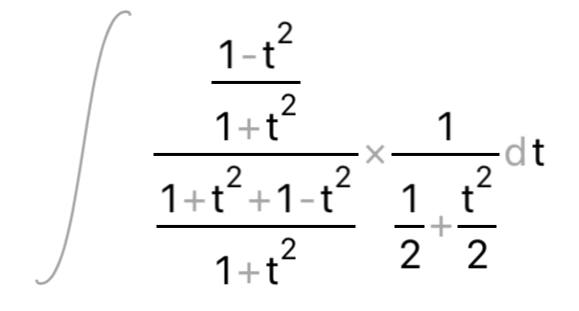 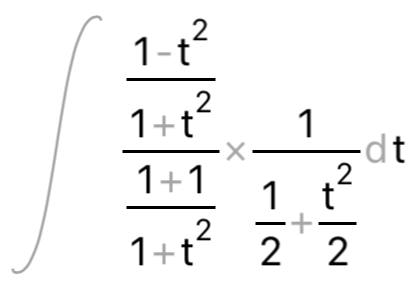  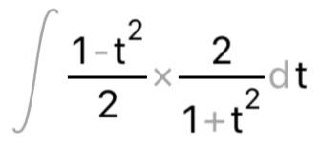 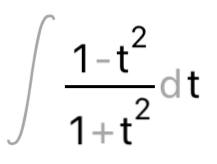 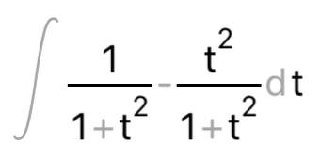 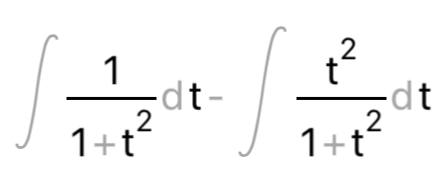 arctan (t) – t + arctan (t) arctan (tan( 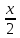 )) – tan ( )) – tan (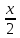 ) + arctan (tan ( ) + arctan (tan (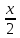 )) ))x – tan ( 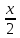 ) )Решение: x – tan ( 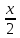 ) + C, C ) + C, C  R R9.5. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж. x2 + 2 y = 0 y = - 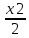 y = - 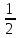 x2 x2a = - 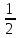 ; h = 0; k = 0 ; h = 0; k = 0x = 0 y = 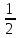   x y x y -2 -2 -1 - 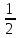 0 0 - 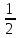 - 2 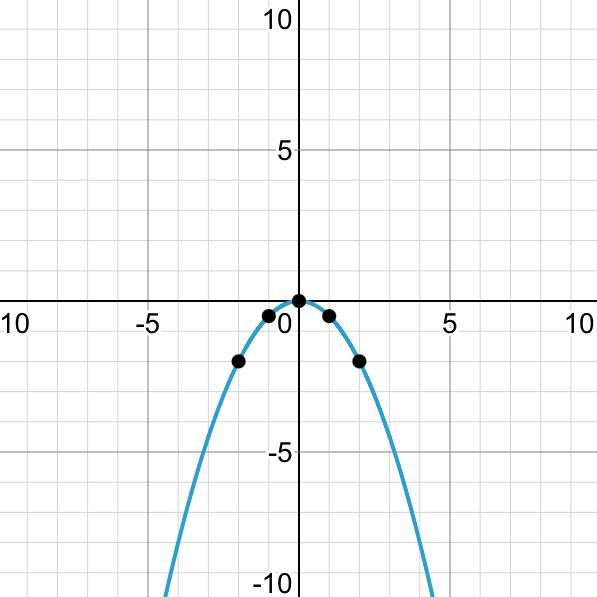 2x – y – 3 = 0 y = 2x – 3 (0, -3)  x y x y - 3 - 1  |
