Решение. Уравнение прямой будем искать по формуле Так как у параллельных прямых угловые коэффициенты равны k1k2, то
 Скачать 220.79 Kb.
|
|
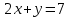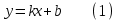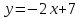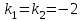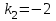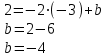Контрольные по математике. Решение задач по математике для студентов. №1 Составить уравнение прямой, которая проходит через точку М(-3,2) и параллельна прямой  Решение. Уравнение прямой будем искать по формуле  Так как у параллельных прямых угловые коэффициенты равны k1=k2 , то   Подставим угловой коэффициент  и точку М(-3,2) в уравнение (1) Искомое уравнение прямой 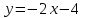 Ответ: 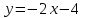№2 Через точку М(2,5) провести прямую так, чтобы ее отрезок, заключенный между осями координат, делится в этой точке пополам. Решение. Пусть данная прямая пересекает ось ОY в точке А(0,а), ось ОХ в точке В(b,0). Координаты середины отрезка АВ (это точка М) равны 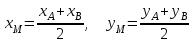 Получим 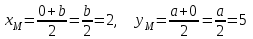 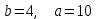 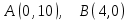 Составим уравнение прямой АВ с помощью формулы 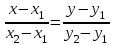 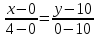 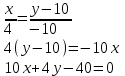 Ответ: 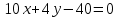 №3 Составить уравнение сторон треугольника, зная одну из его вершин А(-1,3) и уравнения двух высот 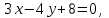 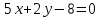 Р ешение. Выполним рисунок 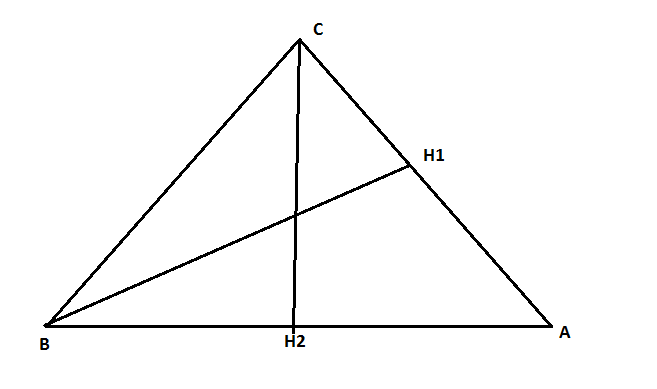 Пусть высота ВН1 имеет уравнение 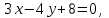а высота СН2 задается уравнением 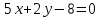Так как известны уравнения высот, то известны координаты нормальных векторов этих высот n1(3; – 4)- нормальный вектор высоты ВН1 и n2(5; 2) - нормальный вектор высоты СН2. Так как стороны треугольника АС и АВ должны быть перпендикулярными этим высотам то для вывода уравнения этих сторон воспользуемся формой уравнения прямой, проходящей через данную точку А(-1,3) в данном направлении: 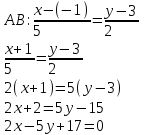 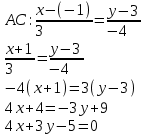 Координаты точки В найдем как точку пересечения прямой АВ и высоты ВН1. Для этого составим систему уравнений 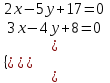 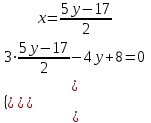 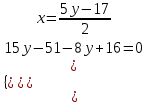 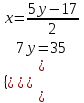 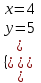 Координаты точки В(4,5) Координаты точки С найдем как точку пересечения прямой АС и высоты СН2. 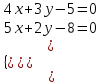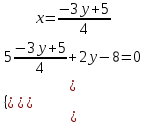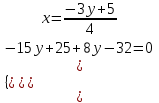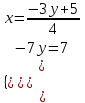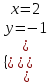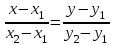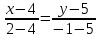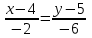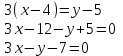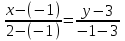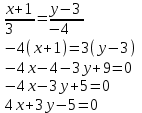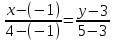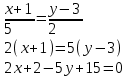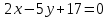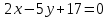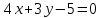Для этого составим систему уравнений      Координаты точки С(2,-1) Уравнение стороны ВС построим, воспользовавшись формой уравнения прямой, проходящей через две заданные точки В(4,5) и С(2,-1)    Уравнение стороны АС, где А(-1,3) и С(2,-1), имеет вид   Уравнение стороны АВ, где А(-1,3) и В(4,5), имеет вид    Ответ: уравнение АВ , уравнение АС  , уравнение ВС 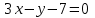 №4 Найти фокальный радиус точки М параболы 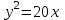 , если абсцисса этой точки равна7.Решение. Фокальный радиус точки параболы найдем по формуле 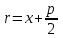 , где х – абсцисса точки М, р – параметр параболыПо условию х=7. Определим параметр р. Так как каноническое уравнение параболы имеет вид 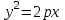 , то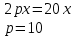 Тогда фокальный радиус равен 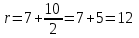 Ответ: 12 №5 Определить вид кривой, найти ее оси, фокусы, уравнения директрис, построить эту кривую 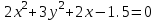 Решение. Для приведения уравнения кривой второго порядка к каноническому виду применим метод выделения полного квадрата. Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при 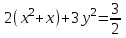 и  вынесем за скобки:  Выделим полный квадрат:  Разделим обе части равенства на 2:  Запишем полученное уравнение в каноническом виде:  Данная кривая – эллипс с центром в точке (-1/2, 0). Найдем ее оси. Большая полуось равна  , малая полуось равна 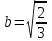 .Фокусы эллипса находятся в точках  и  , где   Тогда  и  Директрисами эллипса называются прямые, определяемые уравнениями  , где   Директрисы равны  Построим данную кривую  Ответ: , , , , ,  №6 Назвать и построить кривую  Решение. Для приведения уравнения кривой второго порядка к каноническому виду применим метод выделения полного квадрата. Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и вынесем за скобки:  Выделим полный квадрат:  Данная кривая есть гипербола с центром в точке (3,-2), с фокусами на оси ординат. Построим данную кривую.  Ответ:  - гиперола№7 Определить вид и параметры поверхности, построить ее методом сечений  Решение.  Данная поверхность – однополостный гиперболоид с центром в точке (-2,0,1), параметры  , вытянутый вдоль оси ОХ.Исследуем поверхность методом параллельных сечений. Будем пересекать поверхность горизонтальными плоскостями  .Подставим в уравнение. Получим При любом таком сечении получаются гиперболы с фокусами на оси ординат , полуосями  , центр в точке (-2,0,0)Подставим  в уравнение. Получим При любом таком сечении получаются эллипсы с фокусами на оси ординат , полуосями  , центр в точке (0,0,1)Подставим  в уравнение. Получим При любом таком сечении получаются гиперболы с фокусами на оси OZ , полуосями  , центр в точке (-2,0,1)Координатные плоскости являются плоскостями симметрии. Поверхность изображена на рисунке  №8 Назвать и построить поверхности а)  б)  Решение. а)  Данная поверхность представляет собой параболический цилиндр, с центром в точке (0,0,1), вытянутый вдоль оси OY.  б) Данная поверхность представляет собой эллиптический параболоид, с центром в точке (1,0,0), вытянутый вдоль оси OZ.  Помощь на экзамене онлайн. |