Контрольная работа 1 Отрезки. Углы 1
 Скачать 51.66 Kb. Скачать 51.66 Kb.
|
|
Контрольная работа №1 «Отрезки. Углы» 1 вариант На луче с началом в точке О отмечены точки А и В. Найдите отрезок АВ, если OА = 10,3 см, OВ = 2,4 см. Какую длину может иметь отрезок АВ? Углы СОА и АОВ – смежные. Угол СОА равен 105º. Чему равен угол АОВ? При пересечении прямых ES и NM в точке О образовались четыре неразвернутых угла. Угол EON равен 61º. Найти углы NOS, SOM, MOE. Один из смежных углов в 4 раза больше другого. Найти оба угла. (доп.) Сумма вертикальных углов NOE и BOS, образованных при пересечении прямых NC и BE, равна 86º. Найдите угол ЕОС. Контрольная работа №1 «Отрезки. Углы» 2 вариант На луче с началом в точке О отмечены точки F и N. Найдите отрезок FN, если OF = 5,6 см, ON = 3,8 см. Какую длину может иметь отрезок FN? Углы EOS и SOD – смежные. Угол EOS равен 65º. Чему равен угол SOD? При пересечении прямых АВ и CD в точке О образовались четыре неразвернутых угла. Угол СОВ равен 123º. Найти углы BOD, DOА, АOC. Один из смежных углов на 70º больше другого. Найти оба угла. (доп.) Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых AD и ВС, равна 108º. Найти угол BOD. …………………………………………………………………………………………………. Контрольная работа № 2 «Равные треугольники» 1 вариант Дано: АО = ВО, СО = DO, СО = 5 см, ВО = 3 см, BD = 4 см. Найти: периметр Δ САО. Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С, так, что 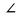 ADB = ADB = 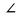 ADC. Доказать, что АВ = АС. ADC. Доказать, что АВ = АС.В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. BD – медиана треугольника. Доказать, что Δ BKD = Δ BMD. (доп.) В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2. Найти стороны треугольника. Контрольная работа № 2 «Равные треугольники» 2 вариант Дано: AB = CD, BC = AD, AC = 7 см, AD = 6 см, АВ = 4 см. Найти: периметр Δ ADC. На сторонах угла D отмечены точки М и К так, что DM = DK. Точка Р лежит внутри угла и РК = РМ. Доказать, что луч DP- биссектриса угла MDK. В равнобедренном ΔАВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. BD - медиана – треугольника. Доказать, что ΔAKD = ΔCMD. (доп.) В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3. Найти стороны треугольника. …………………………………………………………………………………………………….. Контрольная работа № 3 «Параллельные прямые» 1 вариант Дано: а ǀǀ в, с - секущая, 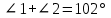 . Найти: все образовавшиеся углы. . Найти: все образовавшиеся углы.Дано: 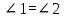 , , 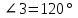 . Найти: . Найти: 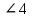 . .Отрезок AD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если 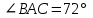 . .Контрольная работа № 3 «Параллельные прямые» 2 вариант Дано: а ǀǀ в, с - секущая, угол 1 больше угла 2 на 400. Найти: все образовавшиеся углы. Дано: 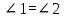 , , 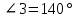 . Найти: . Найти: 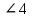 . .Отрезок AК – биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найти углы треугольника AKN, если 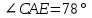 .…………………………………………………………………………………………… .……………………………………………………………………………………………Контрольная работа по геометрии № 4 «Сумма углов треугольника» 1 вариант В Δ АВС АВ > BC > AC. Найти 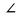 А, А, 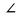 В, В, 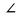 С, если известно, что один из углов треугольника равен 120°, а другой 40°. С, если известно, что один из углов треугольника равен 120°, а другой 40°.В треугольнике АВС угол А равен 50°, а угол В в 12 раз меньше угла С. Найти углы В и С. В треугольнике АВС угол С равен 90°, а угол В равен 35°, CD – высота. Найти углы треугольника ACD. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найти стороны треугольника. (Дополнит.) В треугольнике АВС угол А меньше угла В в три раза, а внешний угол при вершине А больше внешнего угла при вершине В на 40°. Найти внутренние углы треугольника АВС. (Дополнит.) В треугольнике АВС угол С равен 90°, а угол В равен 70°. На катете АС отложен отрезок CD, равный СВ. Найти углы треугольника АВD. Контрольная работа по геометрии № 4 «Сумма углов треугольника» 2 вариант В Δ АВС АВ < BC < AC. Найти 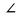 А, А, 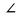 В, В, 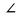 С, если известно, что один из углов треугольника прямой, а другой равен 30°. С, если известно, что один из углов треугольника прямой, а другой равен 30°.В треугольнике АВС угол А равен 90°, а угол С на 40° больше угла В. Найти углы В и С. В треугольнике АВС угол С равен 90°, а угол А равен 70°, CD – биссектриса. Найти углы треугольника ВCD. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найти стороны треугольника. (Дополнит.) В треугольнике АВС угол А меньше угла В в три раза, а внешний угол при вершине А больше внешнего угла при вершине В на 40°. Найти внутренние углы треугольника АВС. (Дополнит.) В треугольнике АВС угол С равен 90°, а угол В равен 70°. На катете АС отложен отрезок CD, равный СВ. Найти углы треугольника АВD. ………………………………………………………………………………………………… Контрольная работа №5 «Прямоугольный треугольник» 1 вариант В треугольнике АВС: 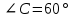 , , 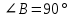 . Высота ВВ1 равна 2 см. Найти АВ. . Высота ВВ1 равна 2 см. Найти АВ.В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найти расстояние от точки О до прямой MN. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найти гипотенузу треугольника. В треугольнике АВС  , , 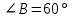 . На стороне АС отмечена точка D так, что . На стороне АС отмечена точка D так, что 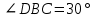 , , 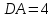 см. Найти АС и расстояние от точки D до стороны ВС. см. Найти АС и расстояние от точки D до стороны ВС.Контрольная работа №5 «Прямоугольный треугольник» 2 вариант В треугольнике АВС: 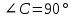 , СС1 – высота, СС1 = 5 см, ВС = 10 см. Найти , СС1 – высота, СС1 = 5 см, ВС = 10 см. Найти 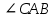 . .В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найти расстояние от точки F до прямой DE. Один из углов прямоугольного треугольника равен 60°, а разность гипотенузы и меньшего катета равна 15 см. Найти гипотенузу треугольника. В треугольнике АВС 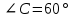 . На стороне АС отмечена точка D так, что . На стороне АС отмечена точка D так, что 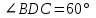 , , 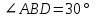 , , 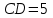 см. Найти АС и расстояние от точки D до стороны АВ. см. Найти АС и расстояние от точки D до стороны АВ.…………………………………………………………………………………………………….. Годовая контрольная работа 1 вариант Дано: ВО = DО, 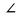 АВС = 45º, АВС = 45º, 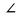 ВСD = 55º, ВСD = 55º, 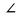 АОС = 100º. АОС = 100º.Найти: 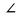 D. D.Доказать: ∆ АВО = ∆ CDO. В равнобедренном треугольнике АВС с основанием АС угол В равен 42º. Найдите два других угла треугольника АВС. В прямоугольном треугольнике АВС с прямым углом С проведена высота СН, причем СН = 8 см, 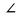 В = 45º. Найдите гипотенузу АВ. В = 45º. Найдите гипотенузу АВ.Годовая контрольная работа 2 вариант Дано: АВ = CD, 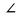 АВС = 65º, АВС = 65º, 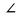 АDС = 45º, АDС = 45º, 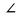 АОС = 110º. АОС = 110º.Найти: 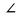 С. С.Доказать: ∆ АВО = ∆ DСO. В равнобедренном треугольнике АВС с основанием АС угол В равен 54º. Найдите два других угла треугольника АВС. В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса ВМ, причем 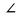 АМВ = 110º. Найдите угол ВАМ. АМВ = 110º. Найдите угол ВАМ.………………………………………………………………………………………………… |
