КР №1. Контрольная работа 1 по дисциплине Физика Вариант 6 Выполнил студент Гр. 320пиитцэб гурова А. С преподаватель Шишкина О. А
 Скачать 208.3 Kb.
|
 Брянский государственный технический университет Кафедра «Общая физика» Направление 09.03.03 «Прикладная информатика», профиль «Информационные технологии в цифровой экономике» Контрольная работа №1 по дисциплине «Физика» Вариант №6 Выполнил студент Гр. 3-20-ПИ-итцэ-Б Гурова А.С Преподаватель: Шишкина О.А Брянск 2022 Содержание Вопрос 1……………………………………………………………………3-5 Вопрос 2……………………………………………………………………6-7 Вопрос 3……………………………………………………………………8-9 Список рекомендуемой литературы………………………………………10 Магнитные поля соленоида и тороида. Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник. Тороид можно рассматривать как длинный соленоид, свернутый в кольцо (рис. 4.1). 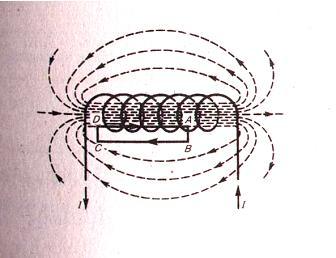 Рис. 4.1. Магнитное поле соленоида Длина соленоида l содержит N витков и по нему протекает ток I. Считаем соленоид бесконечно длинным. Эксперимент показал, что внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю). Циркуляция вектора В по замкнутому контуру, совпадающему с одной из линий магнитной индукции, охватывающему все N витков, согласно (4.12) равна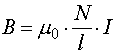:  . (4.14)Интеграл  можно представить в виде суммы двух интегралов: по внутренней части контура: и по внешней:  , тогда из (4.14) получим: , (4.15) или  , (4.16)где В – индукция магнитного поля внутри с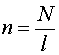оленоида;  – число витков на единицу длины соленоида.Магнитное поле внутри тороида, так же, как в соленоиде, однородно, сосредоточено внутри; вне тороида магнитное поле, создаваемое круговыми токами тороида, равно нулю. Величина магнитного поля в тороиде определяется выражением (4.16), причем длина тороида l берется по средней длине тороида (среднему диаметру). Отметим любопытный факт. Во всех учебниках по физике остался не отмеченным факт существования у соленоида и тороида второго магнитного поля, которое появляется из-за того, что, например, в соленоиде по отношению к средней линии соленоида витки направлены не точно перпендикулярно, а под углом меньше 90°. Это приводит к появлению тока (эффективного, но равного току I, протекающему через соленоид), вдоль соленоида (рис. 4.2). 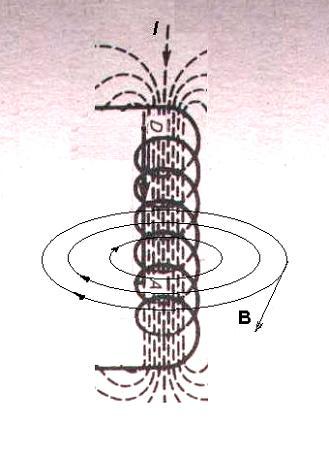 Рис. 4.2. Второе магнитное поле соленоида То есть соленоид создает дополнительное магнитное поле, такое же, как и прямолинейный бесконечно длинный проводник с током. Точно так же и для тороида: вдоль средней линии протекает эффективный ток I. У тороида второе магнитное поле эквивалентно магнитному полю витка с током (рис.4.3). Диаметр этого витка равен диаметру тороида (его средней линии), а магнитное поле 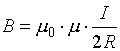тороида  (R – радиус тороида).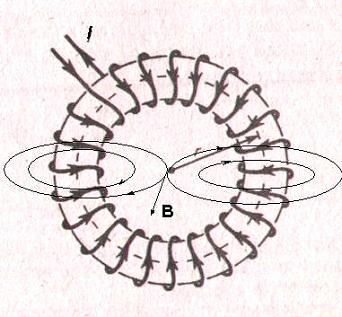 Рис. 4.3. Второе магнитное поле тороида Дифракция Фраунгофера на одной щели. До сих пор мы рассматривали дифракцию лучей, расходящихся от точечного источника. Дифракция света на расходящихся или сходящихся лучах называют дифракцией Френеля. Немецкий ученый И. Фраунгофер (1787 – 1826) исследовал дифракцию в параллельных лучах. Для получения системы параллельных лучей точечный источник света помещается в фокусе собирающей линзы и дифракционная картина исследуется в фокальной плоскости второй собирающей линзы На рис.17 показана схема наблюдения дифракции в параллельных лучах. 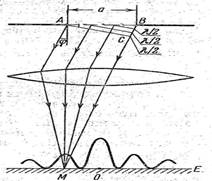 Рис17 На длинную и узкую щель АВ шириной а по нормали падает параллельный пучок монохроматического света. Фронт световых волн параллелен щели. Согласно принципу Гюйгенса, каждая точка фронта волны становится новым источником волн. Поэтому за щелью во всех направлениях распространяются световые волны. Но в одних направлениях дифрагирующие волны усиливают друг друга в других – ослабляют. Чтобы наблюдать дифракционную картину, поместим за щелью собирающую линзу и рассмотрим дифракционную картину на экране Э, помещенную в ее фокальную плоскость. Выберем лучи, отклоненные от первоначального направления на угол φ. Для того чтобы ответить на вопрос, что дадут лучи, отклоненные на угол φ в точке наблюдения М в результате дифракции – максимум или минимум, – нужно знать число зон Френеля, укладывающихся на ширине щели. Если число зон нечетно, значит, в точке М наблюдается максимум, если четно – минимум Чтобы рассчитать число зон Френеля, от крайней точки А опустим перпендикуляр на крайний луч, идущий от другой крайней точки щели В и точку падения перпендикуляра обозначим буквой С. Полученный отрезок ВС разделим на участки равные /2 и через каждый уча20сток проведем плоскости, параллельные перпендикуляру. Эти плоскости разделят волновой фронт АВ на зоны Френеля, число которых равно  .Из треугольника АВС имеем 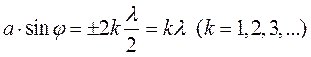 . Тогда, если число зон Френеля четно, то (10)и в точке М наблюдается минимум, если число зон Френеля нечетно, то  (11)В точке М наблюдается максимум освещенности. Расчеты показывают, что результирующая амплитуда колебания 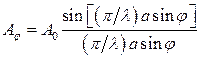 в точке М выражается формулой . (12)Нетрудно проверить, что при  , или  , амплитуда равна нулю, т. е. получается минимум.На рис.17 показано распределение интенсивности света при дифракции от одной щели в зависимости от синуса угла φ. Видно, что наиболее интенсивная полоса света на экране наблюдается против щели (φ =0) и по обе стороны от нее наблюдаются слабые симметричные световые полосы. Фотоэффект. Законы фотоэффекта. Фотоэффект — это явление испускания электронов веществом под действием света. В результате исследований были установлены три закона фотоэффекта: 1. Сила тока насыщения прямо пропорциональна интенсивности светового излучения, падающего на поверхность тела. 2. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности. 3. Если частота света меньше некоторой определенной для данного вещества минимальной частоты, то фотоэффект не происходит. 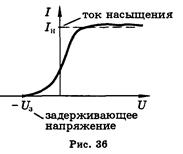 Зависимость фототока от напряжения показана на рисунке 36. Теорию фотоэффекта создал немецкий ученый А. Эйнштейн в 1905 г. В основе теории Эйнштейна лежит понятие работы выхода электронов из металла и понятие о квантовом излучении света. По теории Эйнштейна фотоэффект имеет следующее объяснение: поглощая квант света, электрон приобретает энергию hv. При вылете из металла энергия каждого электрона уменьшается на определенную величину, которую называют работой выхода (Авых). Работа выхода — это работа, которую необходимо затратить, чтобы удалить электрон из металла. Максимальная энергия электронов после вылета (если нет других потерь) имеет вид: mv2/2 = hv — Авых, Это уравнение носит название уравнения Эйнштейна. Если hν < Авых то фотоэффект не происходит. Значит, красная граница фотоэффекта равна νmin = Авых/h Приборы, в основе принципа действия которых лежит явление фотоэффекта, называют фотоэлементами. Простейшим таким прибором является вакуумный фотоэлемент. Недостатками такого фотоэлемента являются: слабый ток, малая чувствительность к длинноволновому излучению, сложность в изготовлении, невозможность использования в цепях переменного тока. Применяется в фотометрии для измерения силы света, яркости, освещенности, в кино для воспроизведения звука, в фототелеграфах и фото телефонах, в управлении производственными процессами. Существуют полупроводниковые фотоэлементы, в которых под действием света происходит изменение концентрации носителей тока. Они используются при автоматическом управлении электрическими цепями (например, в турникетах метро), в цепях переменного тока, в качестве не возобновляемых источников тока в часах, микрокалькуляторах, проходят испытания первые солнечные автомобили, используются в солнечных батареях на искусственных спутниках Земли, межпланетных и орбитальных автоматических станциях. С явлением фотоэффекта связаны фотохимические процессы, протекающие под действием света в фотографических материалах. Список используемой литературы. 1. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Оптика и атомная физика: Учеб. пособие для студ. высш. пед. учеб. заведений. - М.: Издательский центр «Академия», 2000. - 408 с. 3. Ландсберг Г. С. Оптика. Учеб. пособие: Для вузов. – 6-е. изд., стереот. – М.: ФИЗМАТЛИТ, 2003. – 848 с. §§ 39-42. 3. Сивухин Д. В. Общий курс физики. Учеб. пособие: Для вузов. В 5 т. Т. IV. Оптика. — 3-е изд., стереот. — М.: ФИЗМАТЛИТ, 2006. - 792 с. §§ 39-45. 4. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Оптика и атомная физика: Учеб. пособие для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия», 2000. – 408 с. 5. Савельев И.В. Курс общей физики: Учеб. пособие. В 3-х т. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. – 3-е изд. испр. – М.: Наука, Гл. ред. физ. – мат. лит., 1987. – 320 с. |