Тулгу физика КР 1 в22. Физика_КР_1_в-22. Контрольная работа 1 по дисциплине Введение в физику Вариант 22
 Скачать 0.64 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» КОНТРОЛЬНАЯ РАБОТА №1по дисциплине «Введение в физику»Вариант №22
Тула 2021 22.1. Найти модуль разности векторов 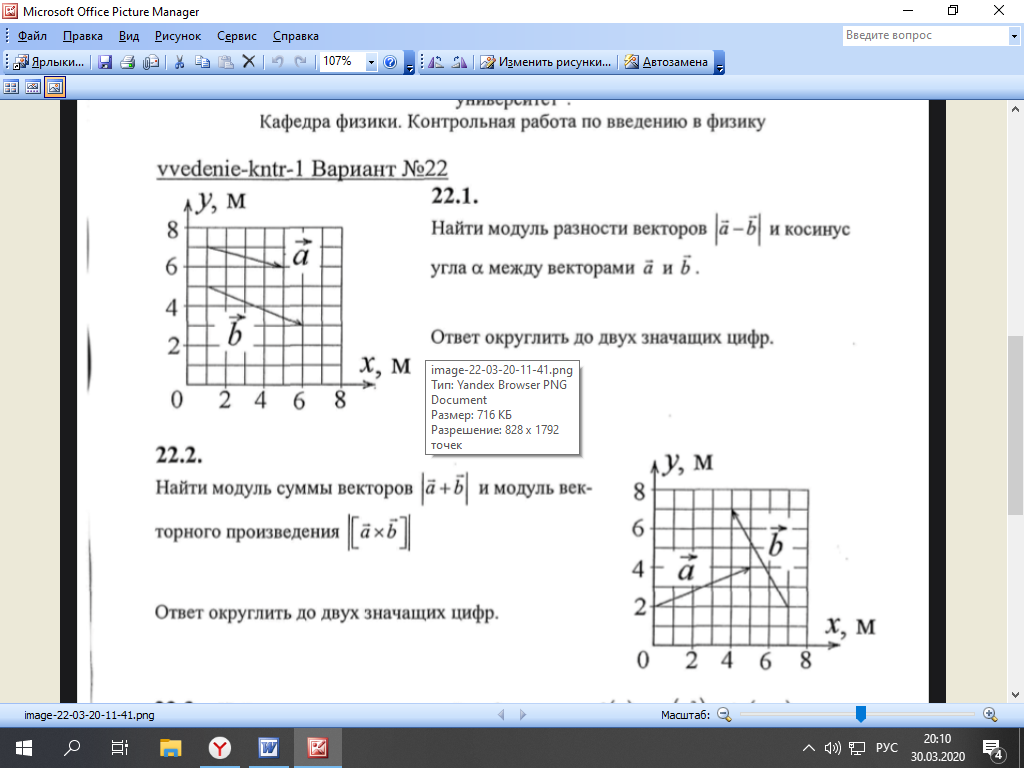 и косинус угла  между векторами  и  Ответ округлить до двух значащих цифр. Решение: Начало вектора :  , конец вектора :  . Координаты вектора  .Начало вектора  :  , конец вектора :  . Координаты вектора  .При вычитании двух векторов, вычитаем поэлементно их координаты: 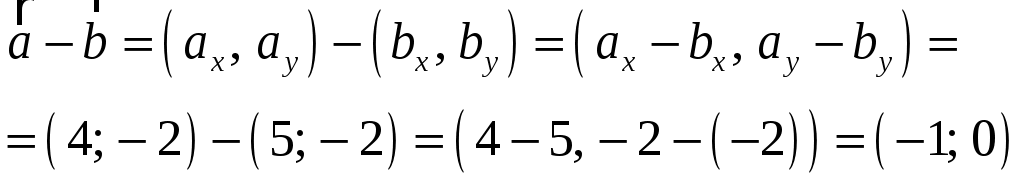 Модуль разности векторов:  Косинус угла 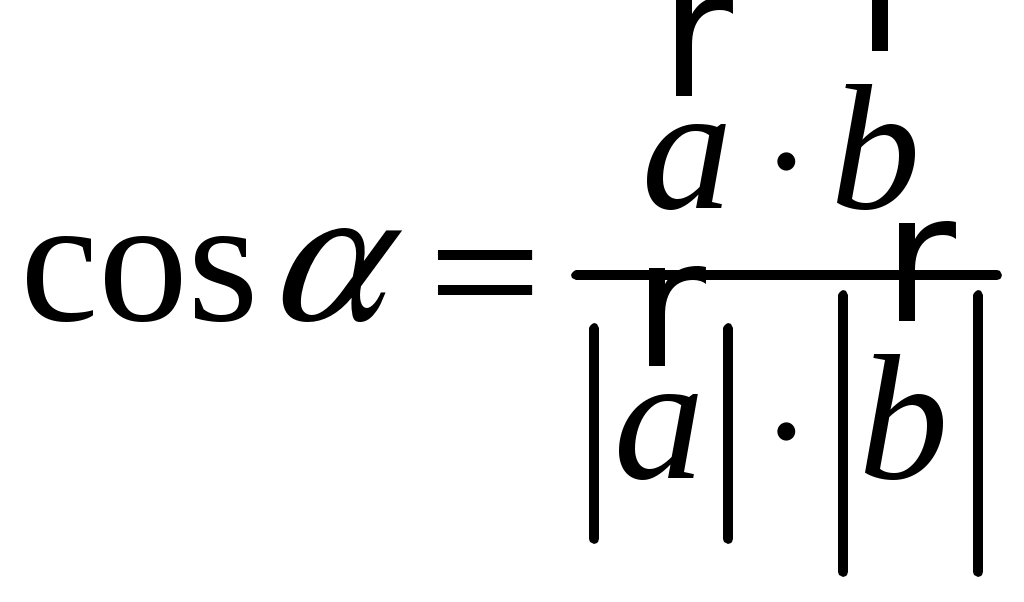между векторами и   Длины векторов: 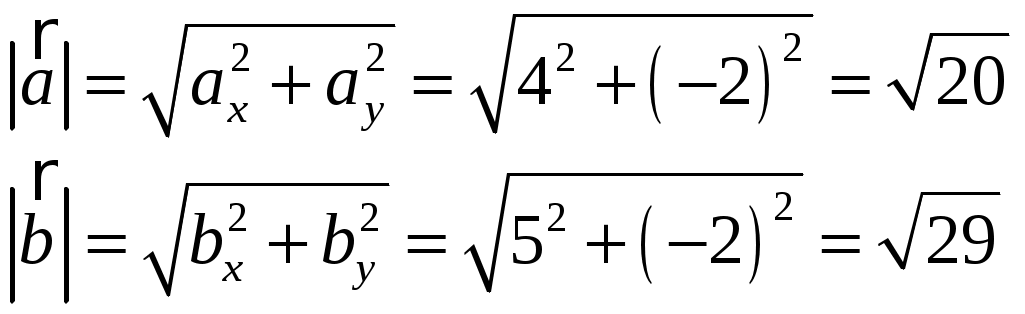 Косинус угла между векторами 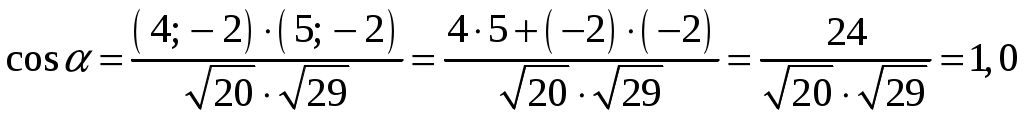и  Ответ:  22.2. Найти модуль суммы векторов  и модуль векторного произведения  .Ответ округлить до двух значащих цифр. 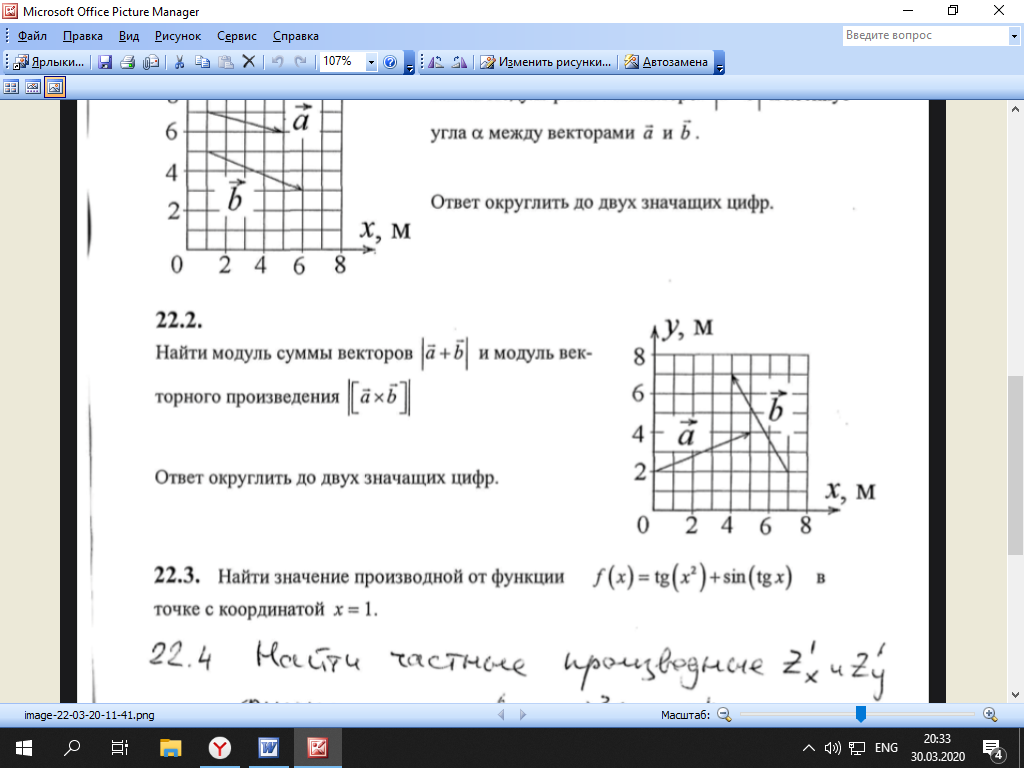 Решение: Начало вектора :  , конец вектора :  . Координаты вектора  .Начало вектора :  , конец вектора :  . Координаты вектора  .При сложении двух векторов, складываем поэлементно их координаты: 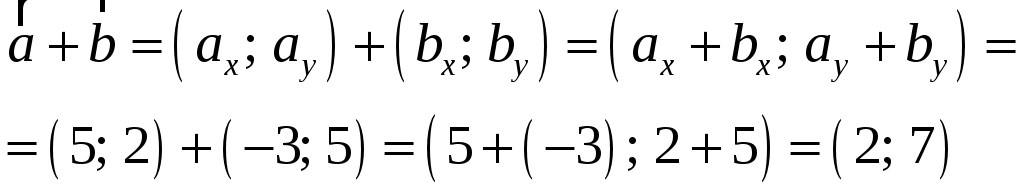 Модуль суммы векторов:  Длины векторов: 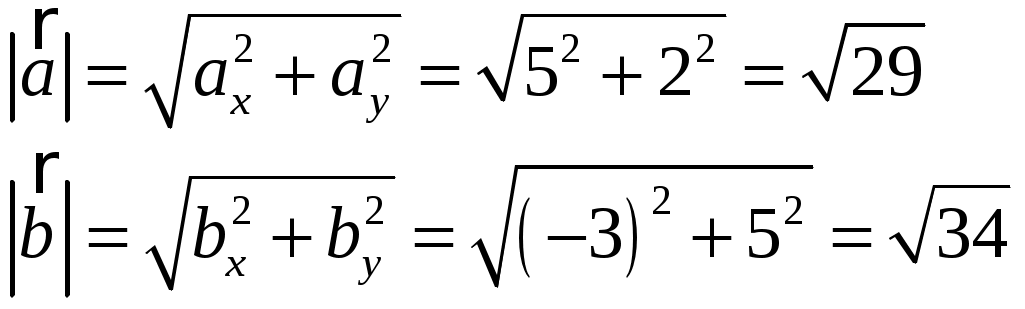 Косинус угла между векторами 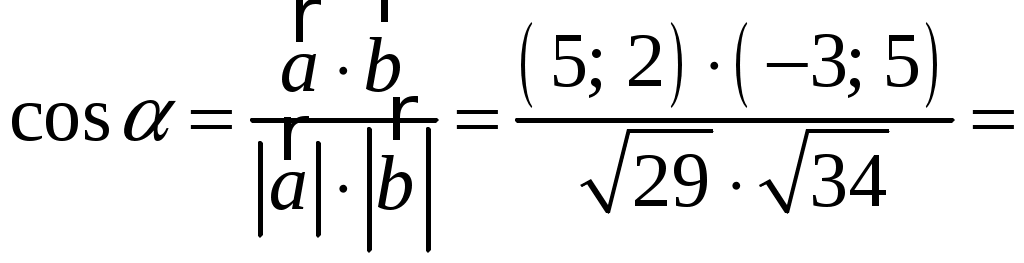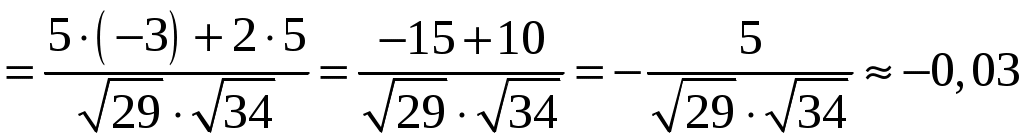и   Используем тригонометрическое равенство  или  Модуль векторного произведения: 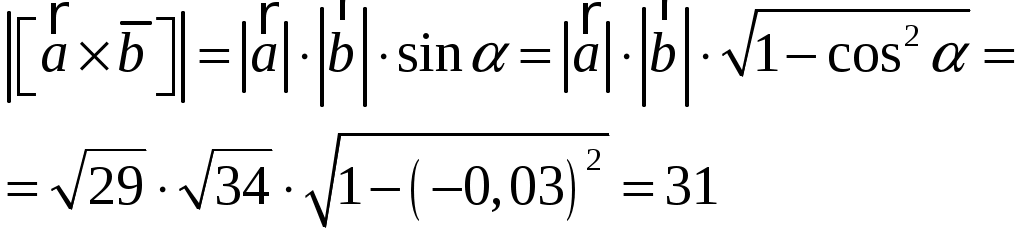 Ответ:  22.3. Найти значение производной от функции  в точке с 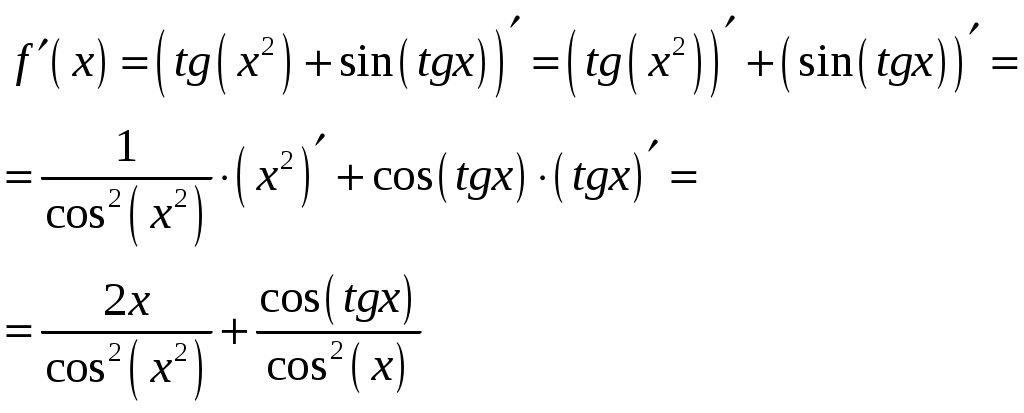координатой  Решение:  Значение производной от функции в точке с координатой 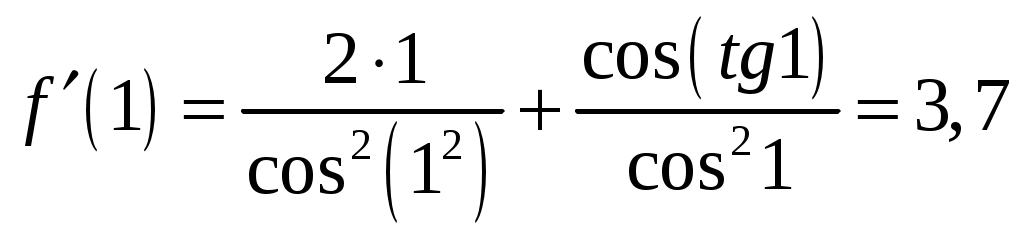  Ответ:  22.4. Найти частные производные  и  функции  Решение: Частные производные находим по обычным формулам дифференцирования для функции одной переменной, причем 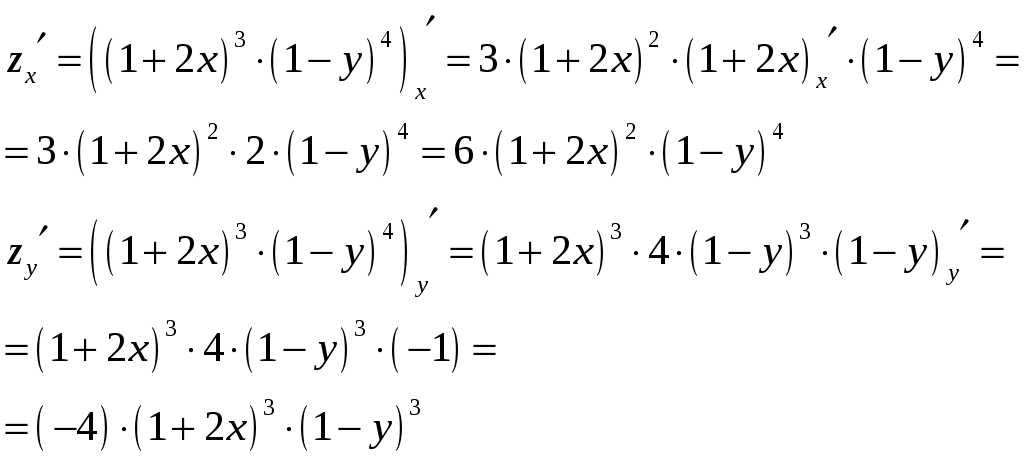находим, считая  постоянной величиной; при отыскании считаем  постоянным: Ответ:  22.5. Найти градиент функции  в точке  .Решение: Найдем частные производные и их значения в точке 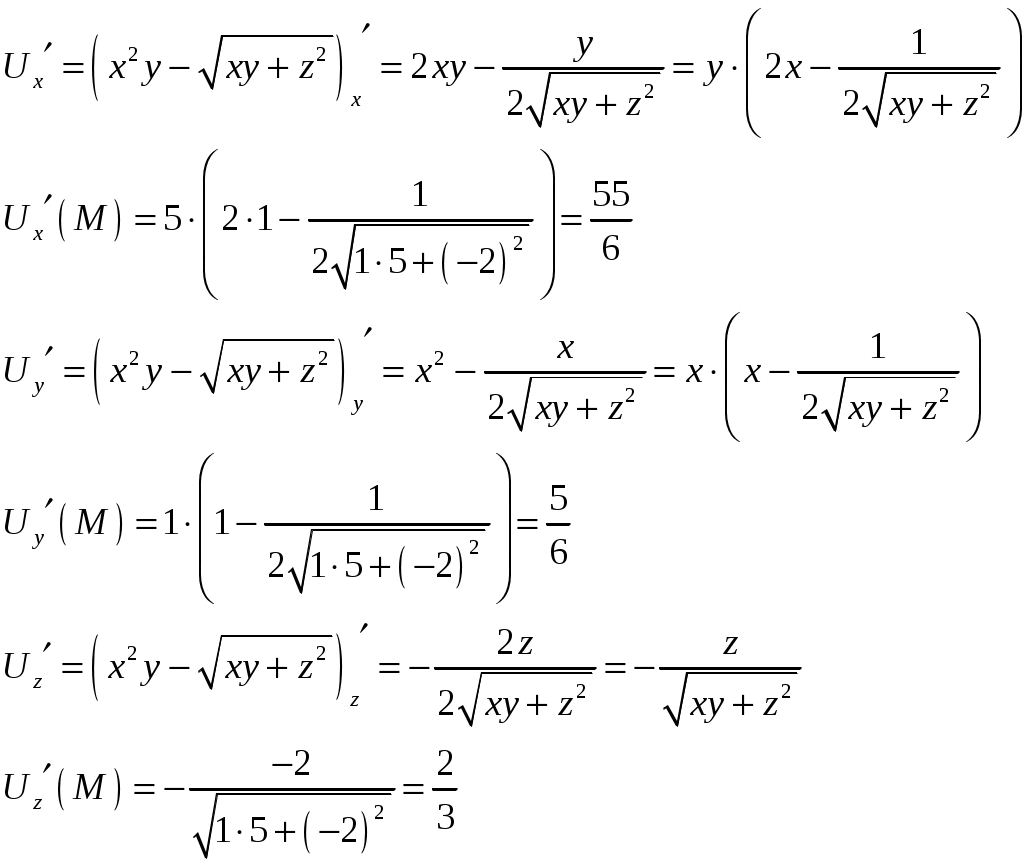 : Градиент функции  в точке   Ответ:  |