|
|
Документ Microsoft Word. Линейными операциями над векторами
1. Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число. Рассмотрим их.
Произведением вектора на число называется вектор, совпадающий по направлению с вектором , если , имеющий противоположное направление, если отрицательное. Длина этого вектора равна произведению длины вектора на модуль числа . Суммой двух векторов и называется вектор , который выходит из их общего начала и является диагональю параллелограмма, стороны которого векторы и . Разностью двух векторов и называют такой вектор, который при сложении с вектором дает вектор . Т.е. если .
Геометрически представляет собой вторую диагональ параллелограмма, построенного на векторах и с общим началом и направленную из конца вектора в конец вектора.
|
3. Комплексным числом называют сумму действительного числа и чисто мнимого числа
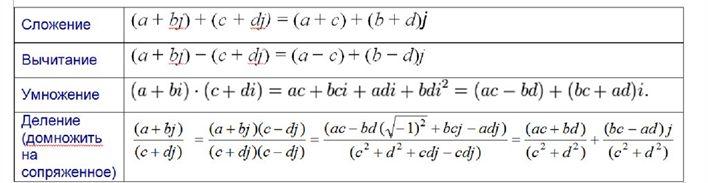
4.
|
6.
7. Условия параллельности двух прямых:
а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k1 = k2 б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.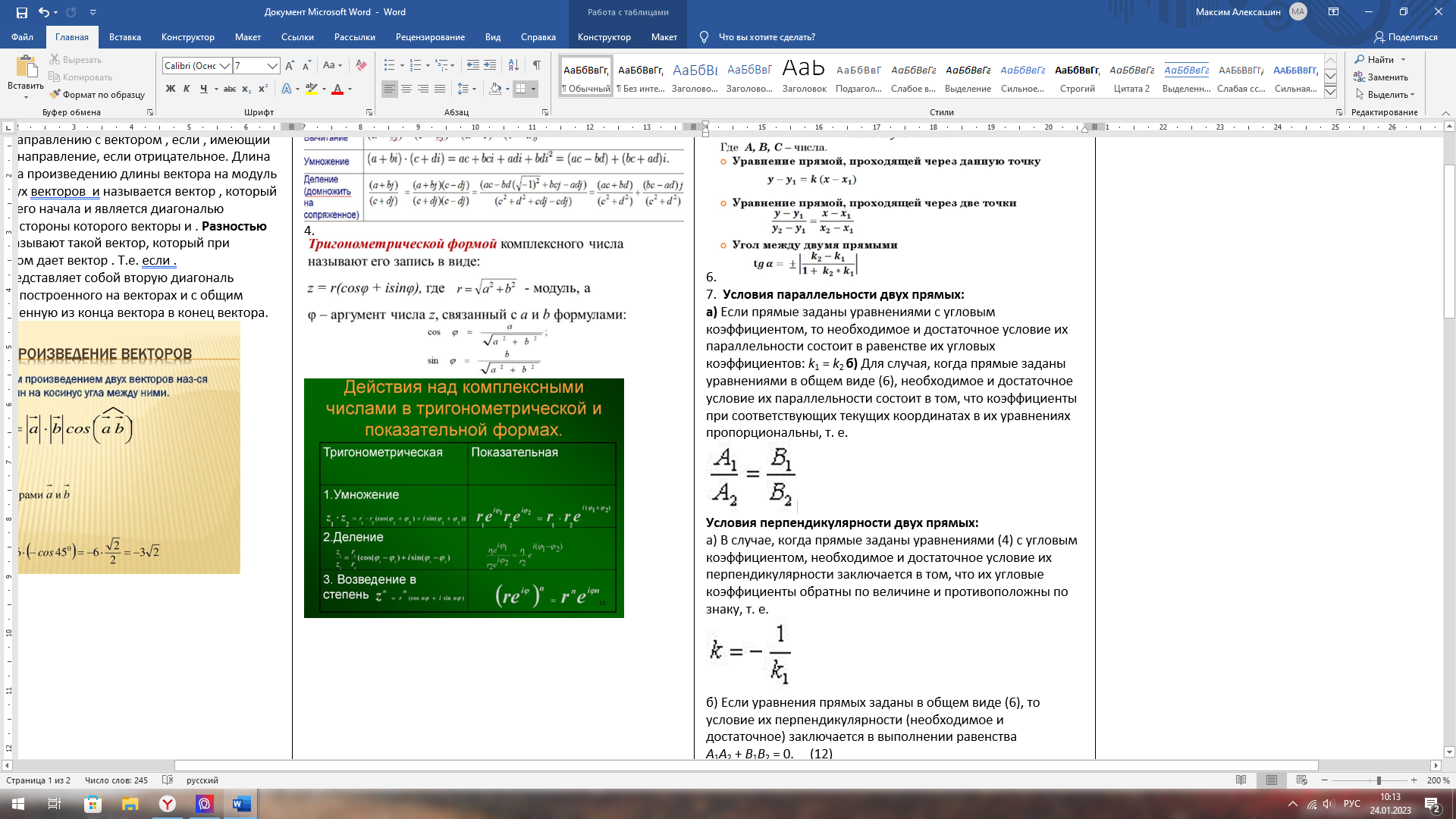
|
Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е. б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
A1A2 + B1B2 = 0.
8. Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей
|
9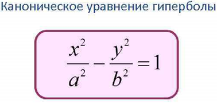 . Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
10. Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки и заданной прямой , не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы.
|
|
13. Матрица - Математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы.
Классификация:
· Матрица, у которой все элементы выше (ниже) главной диагонали равны нулю, называются нижне- (верхнетреугольной) или просто треугольной;
· Матрица, у которой равное число строк и столбцов называют квадратной. Квадратная матрица размера  называется квадратной матрицей порядка n;
· Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной;
· Диагональная матрица, у которой все элементы главной диагонали равны между собой, называется скалярной;
· Скалярная матрица, у которой все элементы главной диагонали равны 1, называют единичной матрицей и обозначают как Е;
· Матрица  называется вектор-строкой длины n, а матрица  – вектор-столбцом длины n.
Если у матрицы поменять местами строки и столбцы, то такая матрица называется транспонированной.
|
|
18. Линейные операции над векторами удовлетворяют следующим свойствам:
1. Х + У = У + Х; (коммутативное свойство суммы)
2. (Х + У) + Z = X + (Y + Z); (ассоциативное свойство суммы)
3. a(bX) = (ab)X;
4. a(X + Y) = aX + aY; (дистрибутивное свойство)
5. (a + b)X = aX + bX;
6. Существует нулевой вектор О=(0,0,…0) такой, что Х + О = Х, для любого Х;
7. Для любого вектора Х существует противоположный вектор (-Х) такой, что Х + (-Х) = О;
8. 1∙Х = Х для любого Х.
|
19. Ранг матрицы. Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 0.
Теорема. Ранг матрицы равен числу ее линейно независимых строк и столбцов. Базисные строки и столбцы любой матрицы линейно независимы, а все другие ее строки и столбцы являются линейными комбинациями базисных строк и столбцов.
21.Зависимость векторов. Векторы x, y, ..., z называются линейно зависимыми векторами, если существуют числа α, β, ..., γ, из которых хотя бы одно отлично от нуля, такие что справедливо равенство: αx+βy+...+γz=0. (0). Другими словами линейная зависимость группы векторов означает, что существует среди них вектор, который можно представить линейной комбинацией других векторов этой группы.
22. собственный вектор – это такой вектор, который под действием линейного оператора переходит в коллинеарный вектор, т.е. просто умножается на некоторое число.
|
|
| |
|
|
Скачать 2.79 Mb.