задачи метрология. МСиС КР 6 вариант (Сенько). Контрольная работа 1 по предмету Метрология, стандартизация и сертификация Выполнил студент Синько В. Е
 Скачать 106.63 Kb. Скачать 106.63 Kb.
|
 Министерство цифрового развития, связи И массовых коммуникаций российской федерации Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования Московский технический университет связи и информатики Кафедра «Метрологии, стандартизации и измерений в инфокоммуникациях» Контрольная работа №1: по предмету «Метрология, стандартизация и сертификация» Выполнил студент: Синько В.Е. Группа БСТ1854 Проверено: _____________________ Задание 1. Показание цифрового (электронно-счетного) измерителя частоты при измерении периода N. Найти максимальную абсолютную и относительную погрешности дискретности. Исходные данные: Вариант 6. N = 78,1 мкс Решение: Цифровые методы измерителя частоты при измерении периода сводятся к подсчету числа импульсов за интервал времени. Режимы работы цифрового частотомера (режим «измерения частоты» или режим «измерения периода») отличаются тем, как (из чего) формируются считаемые импульсы и интервалы, за которые они считаются. В режиме измерения периода (рис.1.1) неизвестным является интервал Тх, а считаемые импульсы устанавливаются с известной частотой, т.е. известным периодом Т0.  Рис. 1.1. Пояснение возникновения погрешности дискретности. Тх – рассматриваемый интервал; Ти – результат измерения этого интервала. Число на счетчике 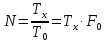 Если, F0 равна 1 Гц , то измеряемый период будет измерен в секундах, если F0 = 1 МГц, то в микросекундах и.т.д. При таких подсчетах импульсов за интервал появляется так называемая погрешность дискретности. Рассмотрим как она появляется (рис.1.1). Из рисунка видно, что Тх = Ти + ∆1 + ∆2, где ∆1 + ∆2 = D и является погрешность дискретности. Эта погрешность случайна, распределена по равномерному закону в интервале от 0 до  ∆мах. Из рисунка видно, что ∆мах. Из рисунка видно, что  ∆мах = 2Т0 , то есть удвоенному периоду счетных импульсов. ∆мах = 2Т0 , то есть удвоенному периоду счетных импульсов.Рассматриваем полученное в результате измерения число: 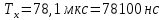 Выбираем период метки 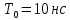 Число импульсов: 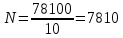 Максимальная абсолютная погрешность: 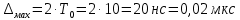 Максимальная относительная погрешность: 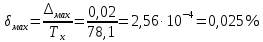 Рассмотрим способы уменьшения погрешности дискретности. 1. Если синхронизовать счетные импульсы с началом интервала измерения, то эта погрешность будет равна 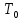 , так как ∆1 = 0. , так как ∆1 = 0.2. При увеличении частоты счетных импульсов уменьшится абсолютное значение погрешности дискретности ( 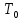 станет меньше). станет меньше).3. При увеличении времени измерений в К раз (с помощью делителя) при той же абсолютной погрешности уменьшается относительная погрешность, так как δ = Т0/КТ. Ответ: 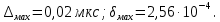 Задание 2. Измеряется напряжение в виде периодической последовательности прямоугольных импульсов с параметрами: длительность импульсов τ, период Т, амплитуда 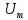 . .Найти чему равно: 1. Показание пикового вольтметра с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 2. Показание пикового вольтметра с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 3. Показание квадратичного вольтметра с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 4. Показание вольтметра средневыпрямленных значений с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 5. Показание вольтметра средневыпрямленных значений с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 6. Показание пикового вольтметра с закрытым входом, проградуированного в максимальных значениях синусоидального сигнала. 7. Показание пикового вольтметра с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. Исходные данные: Вариант 6. Т = 60 мкс; τ = 15 мкс; Um = 30 В. Решение: Рассматриваем последовательность однополярных импульсов. Описывающая функция: 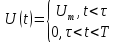 Скважность: 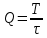 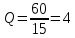 Коэффициент амплитуды: 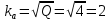 Коэффициент формы: 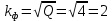 Среднеквадратическое значение напряжения 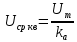 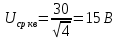 Cредневыпрямленное значение напряжения: 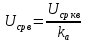 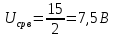 Среднее значение напряжения: 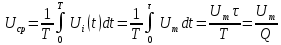 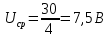 Определяем показание вольтметров. 1. Показание пикового вольтметра с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 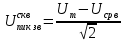 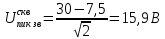 2. Показание пикового вольтметра с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 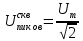 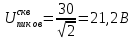 3. Показание квадратичного вольтметра с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. Рассмотрим переменную составляющую сигнала. 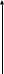 Um Uср в   τ Т t τ Т tРис. 2.1 Постоянная (черный цвет) и переменная (красный цвет) составляющая входного сигнала. Среднеквадратическое значение напряжения 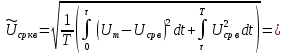 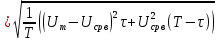 Показание квадратичного вольтметра с закрытым входом: 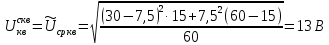 4. Показание вольтметра средневыпрямленных значений с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 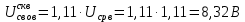 5. Показание вольтметра средневыпрямленных значений с закрытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. средневыпрямленное значение напряжения: 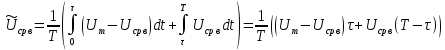 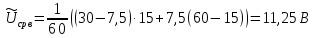 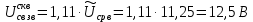 6. Показание пикового вольтметра с закрытым входом, проградуированного в максимальных значениях синусоидального сигнала. 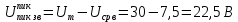 7. Показание пикового вольтметра с открытым входом, проградуированного в среднеквадратических значениях синусоидального сигнала. 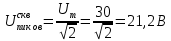 Ответ: 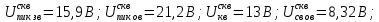 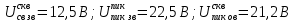 Задание 3. На экране осциллографа наблюдается периодическая последовательность прямоугольных импульсов с периодом Т. Развертка внешняя, длительность развертки 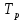 . Нарисовать картинку, которая будет на экране осциллографа при внешней и внутренней синхронизации, считая, что в канале «Y» отсутствует линия задержки. . Нарисовать картинку, которая будет на экране осциллографа при внешней и внутренней синхронизации, считая, что в канале «Y» отсутствует линия задержки.Исходные данные: Вариант 6. Т = 50 мкс; Тр = 300 мкс; Решение: В электронном осциллографе имеется задержка начала горизонтальной развертки из-за инерционности блоков синхронизации. Для согласования исследуемого сигнала с началом горизонтальной развертки в канале Y предусмотрена линия задержки ЛЗ. Она задерживает входной сигнал на время tз и компенсирует, таким образом, задержку появления развертки в канале Х При отсутствии линии задержки на осциллограмме нельзя будет наблюдать начало входного сигнала (например, передний фронт импульсного сигнала). Найдем отношение: Тр /T = 300/50 = 6 Изобразим входной сигнал и сигнал развертки при найденном отношении. 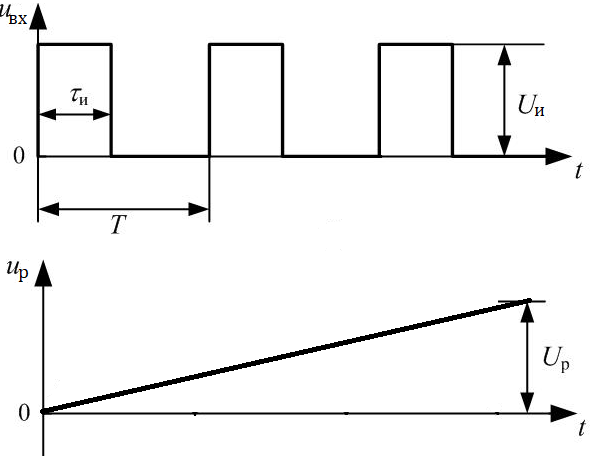 Uвх – напряжение сигнала; Up – пилообразное напряжение развертки; Рис. 3.1 Соотношение входного сигнала и сигнала развертки Отношение Тр /T – целое, поэтому последовательность импульсов отобразится без искажений. 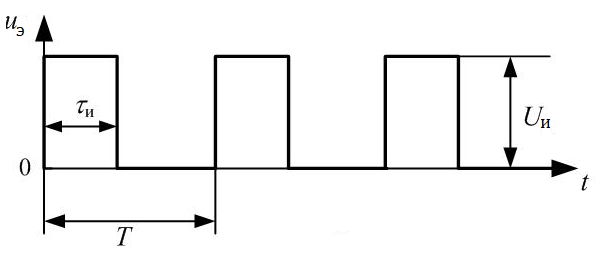 Рис. 3.2 Изображение на экране осциллографа. Задание 4. Цифровым фазометром измеряется фазовый сдвиг синусоидального сигнала с частотой f. Период счетных импульсов 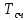 . Определить разрешающую способность (минимальное значение фазы), которое может быть измерено в данном случае. . Определить разрешающую способность (минимальное значение фазы), которое может быть измерено в данном случае.Исходные данные: Вариант 6. f = 30 кГц; Тсч = 10 мкс; Решение: Фазовый сдвиг синусоидального сигнала означает измерении разности начальных фаз двух колебаний одинаковой частоты: 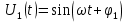 и и 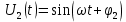 т.е. 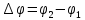 Графически это можно изобразить, как показано на рисунке 4.1 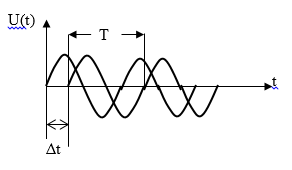 Рис. 4.1 Схема измерения фазового сдвига. Фазовый сдвиг, измеряемый фазометром, определяется соотношением: 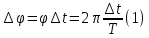 где 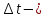 сдвиг сигналов во времени, соответствующего их идентичным фазам; сдвиг сигналов во времени, соответствующего их идентичным фазам;Т – период измеряемого сигнала. Период и частота связаны зависимостью: 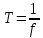 Подставим в (1): 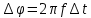 Это же соотношение действует для минимальных величин: 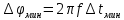 Минимальное время счетчика есть время счета. 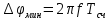 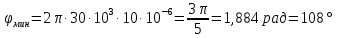 Ответ: 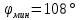 Задание 5. При исследовании спектра периодической последовательности прямоугольных радиоимпульсов длительностью 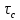 и периодом Т на анализаторе спектра последовательного действия с индикатором на электроннолучевой трубке была получена изображенная ниже картинка. Период развертки анализатора спектра и периодом Т на анализаторе спектра последовательного действия с индикатором на электроннолучевой трубке была получена изображенная ниже картинка. Период развертки анализатора спектра 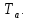 Определить значения Определить значения 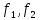 и выразить их в единицах измерения частоты, и число вертикальных полос N. и выразить их в единицах измерения частоты, и число вертикальных полос N. Рис. 5.1 Спектр сигнала для задачи. Исходные данные: Вариант 6. τс = 7мкс; Т = 70 мкс; Та = 1400 мкс; Решение: Из теории спектрального анализа известно, что огибающая спектра подчиняется закону арочного синуса:  Так как сигналы периодические, спектр должен быть линейчатым с расстоянием между линейками равным   Число полос равно количеству сигналов, пришедших за время длительности развертки: 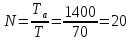 Функция (1) обращается в ноль при x = π, 2π, 3π..... Расстояние между двумя минимумами: 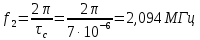 Ответ: 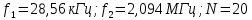 Список использованных источников 1. Хромой Б.П. Метрология и измерения в телекоммуникационных системах (том 1) - М.: ИРИАС, 2007.- 544 с. 2. Хромой Б.П., Кандинов А.В., Сенявский А.Л. и др. Метрология, стандартизация и измерения в технике связи: Учебное пособие, - М.: Издательство «Радио и связь», 1986, 422 с. 3. Сенявский А.Л. Метрология, стандартизация и сертификация. Конспект лекций. М.: Издательсто ООО «Инсвязьиздат», 2009. – 94 с. 4. Сенявский А.Л. Метрология, стандартизация и сертификация. Лекционный курс для студентов-заочников, М.: Издательсто ООО «Инсвязьиздат», 2008. – 38 с. Москва 2022 |
