Лабораторная. Лаба 11. Контрольная работа 11 по дисциплине Математические модели и методы Студент гр. Зпи219 Константинов Н. А. Проверили
 Скачать 71.88 Kb. Скачать 71.88 Kb.
|
|
Министерство науки и образования РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский государственный энергетический университет» Кафедра «Инженерная кибернетика» Контрольная работа №11 по дисциплине «Математические модели и методы» Выполнил: Студент гр. ЗПИ-2-19 Константинов Н.А. Проверили: к.т.н., доцент Косулин В.В. Казань 2021Вариант 6 Задача: Найти решение оптимальной задачи симплекс-методом: 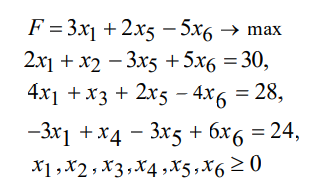 Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции F(x) = 3x1+2x5-5x6 при следующих условиях-ограничений. 2x1+x2-3x5+5x6=30 4x1+x3+2x5-4x6=28 -3x1+x4-3x5+6x6=24 Расширенная матрица системы ограничений-равенств данной задачи: 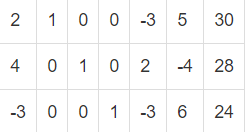 1. В качестве базовой переменной можно выбрать x2. 2. В качестве базовой переменной можно выбрать x3. 3. В качестве базовой переменной можно выбрать x4. Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (2,3,4). Выразим базисные переменные через остальные: x2 = -2x1+3x5-5x6+30 x3 = -4x1-2x5+4x6+28 x4 = 3x1+3x5-6x6+24 Подставим их в целевую функцию: F(x) = 3x1+2x5-5x6 2x1+x2-3x5+5x6=30 4x1+x3+2x5-4x6=28 -3x1+x4-3x5+6x6=24 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: A= 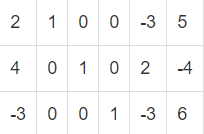 Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x2, x3, x4 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,30,28,24,0,0) Базисное решение называется допустимым, если оно неотрицательно.  1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (30 : 2 , 28 : 4 , - ) = 7 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (4) и находится на пересечении ведущего столбца и ведущей строки.  4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x1 в план 2 войдет переменная x5. Строка, соответствующая переменной x5 в плане 2, получена в результате деления всех элементов строки x1 плана 1 на разрешающий элемент РЭ=1/2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x5 записываем нули. Таким образом, в новом плане 2 заполнены строка x5 и столбец x5. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
1. Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 0, x2 = 72, x3 = 0, x4 = 66, x5 = 14, x6 = 0 F(x) = 3*0 + 2*14 -5*0 = 28 |
