Дать определение функции и пояснить его

• Название: Дать определение функции и пояснить его
• Дата: 18.01.2019
• Размер: 1.36 Mb.
• Имя файла: 1-8.docx
• Тип: Документы; #64281

1. 
   Дать определение функции и пояснить его.
   

Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единсвенное значение переменной у.

х-независимая переменная или аргумент .

У- зависимая переменная или значение функции.

2. 
   Описать основные условия обозначения ( кванторы), применяемые в математическом анализе.
   

3. 
   Дать определение и пояснить понятие сложной функции.
   

Определение. Если на некотором промежутке Х определена функция z = φ(x) с множеством значений Z и на множестве Z определена функция у = f(z), то функция у = f[φ(x)] называется сложной функцией от x (или суперпозицией функций), а переменная z — промежуточной переменной сложной функции.

Определение. Пусть функция определена на множестве, а функция– на множестве, причем множество значений функциисодержится в области определения функции.Поставим в соответствие каждому числуизчисло. Тем самым на множествебудет задана функция. Эту функцию называют сложной функцией или композицией функцийи.

При этом называют внешней, a— внутренней функцией композиции.

4. 
   Описать и привести примеры функций натурального аргумента.
   

Функцию y = f(x), x Є N, называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или y₁, y₂, y₃, …, yn, … . Значения y₁, y₂, y₃ (и т.д.) называют соответственно первым, вторым, третьим (и т.д.) членами последовательности. В символе yn число n называют индексом, который задает порядковый номер того или иного члена последовательности.Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный. формула ее n-го члена: yn = f(n).

Пример. yn = 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

5. 
   Дать определение и привести примеры обратной функции.
   

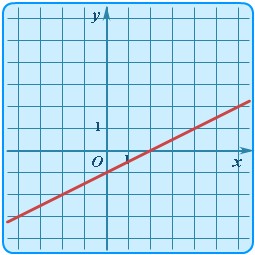
Определение обратной функции.

Пусть функция формула строго монотонная (возрастающая или убывающая) и непрерывная на области определения формула, область значений этой функции формула, тогда на интервале формула определена непрерывная строго монотонная функция формула с областью значений формула, которая является обратной для формула.

Другими словами, об обратной функции формула для функции формула на конкретном промежутке имеет смысл говорить, если на этом интервале формула либо возрастает, либо убывает.

Пример : Найти функцию обратную для .

Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение относительно x ).

- это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать .

Таким образом, и - взаимно обратные функции.

Приведем графическую иллюстрацию взаимно обратных линейных функций.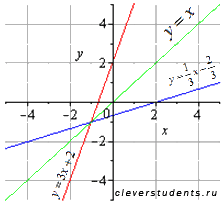


Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов). Это одно из свойств взаимно обратных функций, о которых речь пойдет ниже.

6. 
   Линейная, квадратичная и степенная функции и их графики , как частные случаи целой рациональной функции.
   

Линейная	y = kx + b		Прямая	Общий случай линейной зависимости: коэффициенты k и b - любые действительные числа. К –tg угла наклона К >0 возраст К <0 убыв B<0 полож B>0 отриц B=0 через начало координат
Квадратичная	y = ax2 + bx + c, где a,b,c принадлежат R		Парабола	Общий случай квадратичной зависимости: коэффициент a - произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c - любые действительные числа.

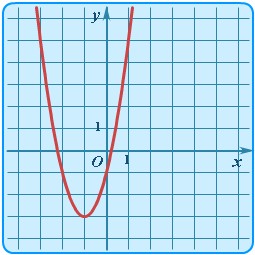
Степенная функция. Это функция:y = axⁿ, где  a , n – постоянные. При  n = 1 получаем прямую пропорциональность:  y = ax; при  n = 2 - квадратную параболу; при  n = 1 - обратную пропорциональность или гиперболу.Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, следовательно, при  n = 0 степенная функция превращается в постоянную величину:  y = a, т.e. её график - прямая линия, параллельная оси  Х, исключая начало координат ( поясните, пожалуйста, почему ? ). Все эти случаи ( при  a = 1 ) показаны на рис.13  ( n 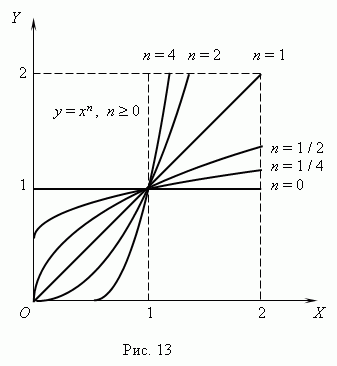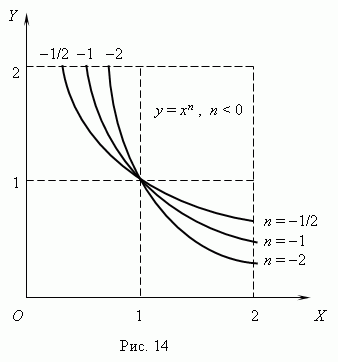0 ) и рис.14 ( n < 0 ). Отрицательные значения  x здесь не рассматриваются, так как тогда некоторые функции:





Если  n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли  n  чётным числом или нечётным. На рис.15 показаны две такие степенные функции:  для  n = 2  и  n = 3.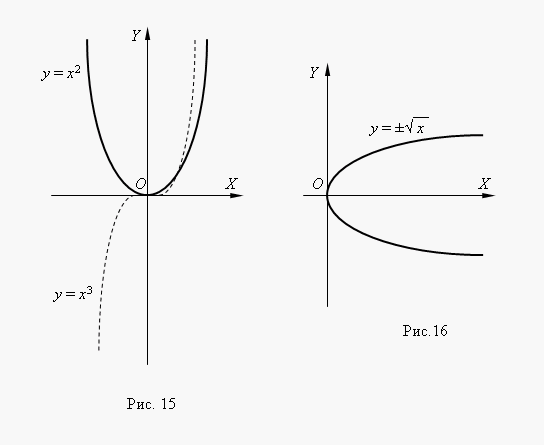



При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция  y = x ³ называется кубической параболой.

На рис.16 представлена функция . Эта функция является обратной к квадратной параболе y = x ², её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного углаЭто способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция ( об этом говорит и знак    перед квадратным корнем ). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей:  верхнюю или нижнюю.

Степенная функция определена для любых х , если m является нечётной числами принадлежит натуральным числам и только для не отрицательных если а является чётным числом принадлежащим множеству натуральных . а принадлежит Z ( МНОЖЕСТВА ЦЕЛЫХ ЧИСЕЛ ОТРИЦАТЕЛЬНЫХ ИЛИ ПОЛОЖИТЕЛЬНЫХ ЧИСЕЛ ), то функция рациональная , если а является дробными членами то есть а не принадлежит Z, то иррациональная .

7. 
   Показательная и логарифмическая функции и их графики.
   

Основные свойства показательной функции

1.Область определения множество действительных чисел.

2.Область значений -множество всех положительных действительных чисел.

3.При a> 1 функция возрастает на всей числовой прямой, при 0 < a< 1 функция убывает на множестве R

(см. рис.1, 2)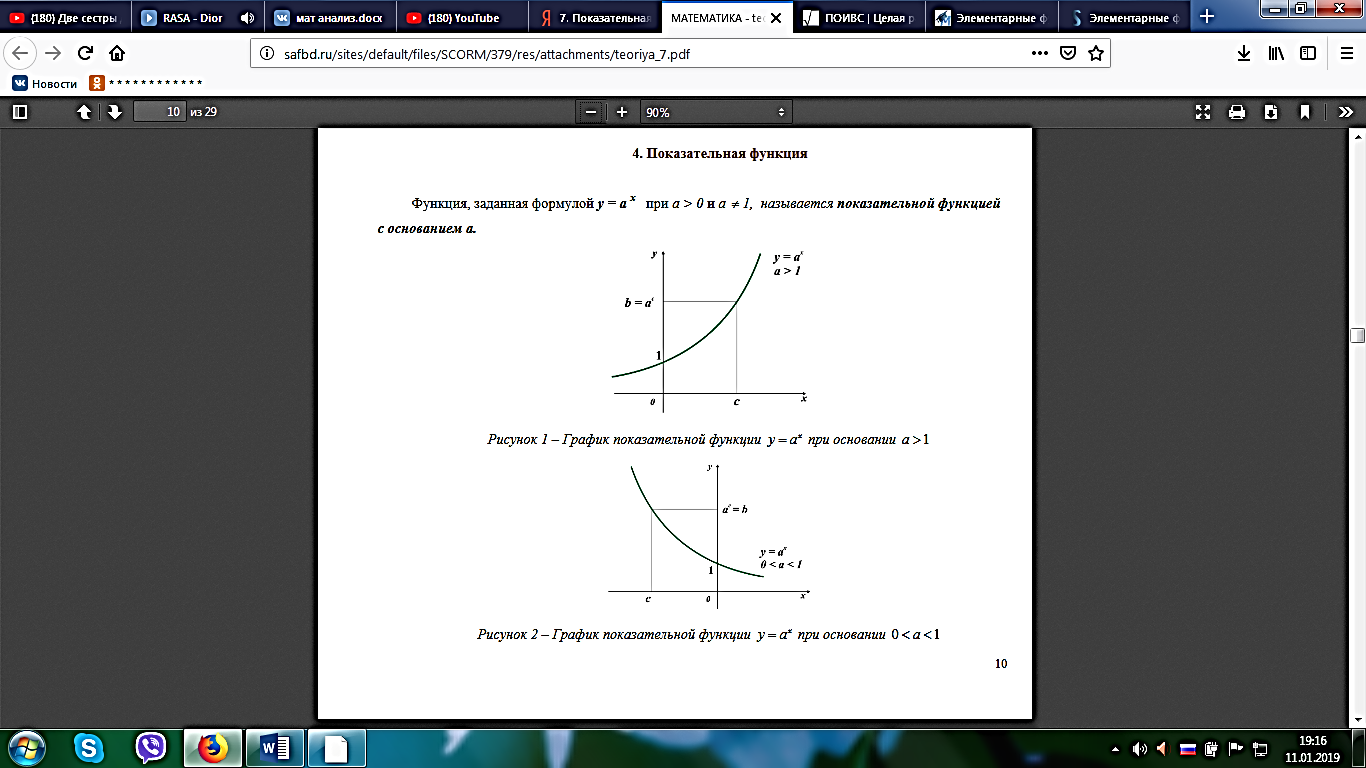

.



Функцию, заданную формулой y= logax, называютлогарифмической функцией с основанием a.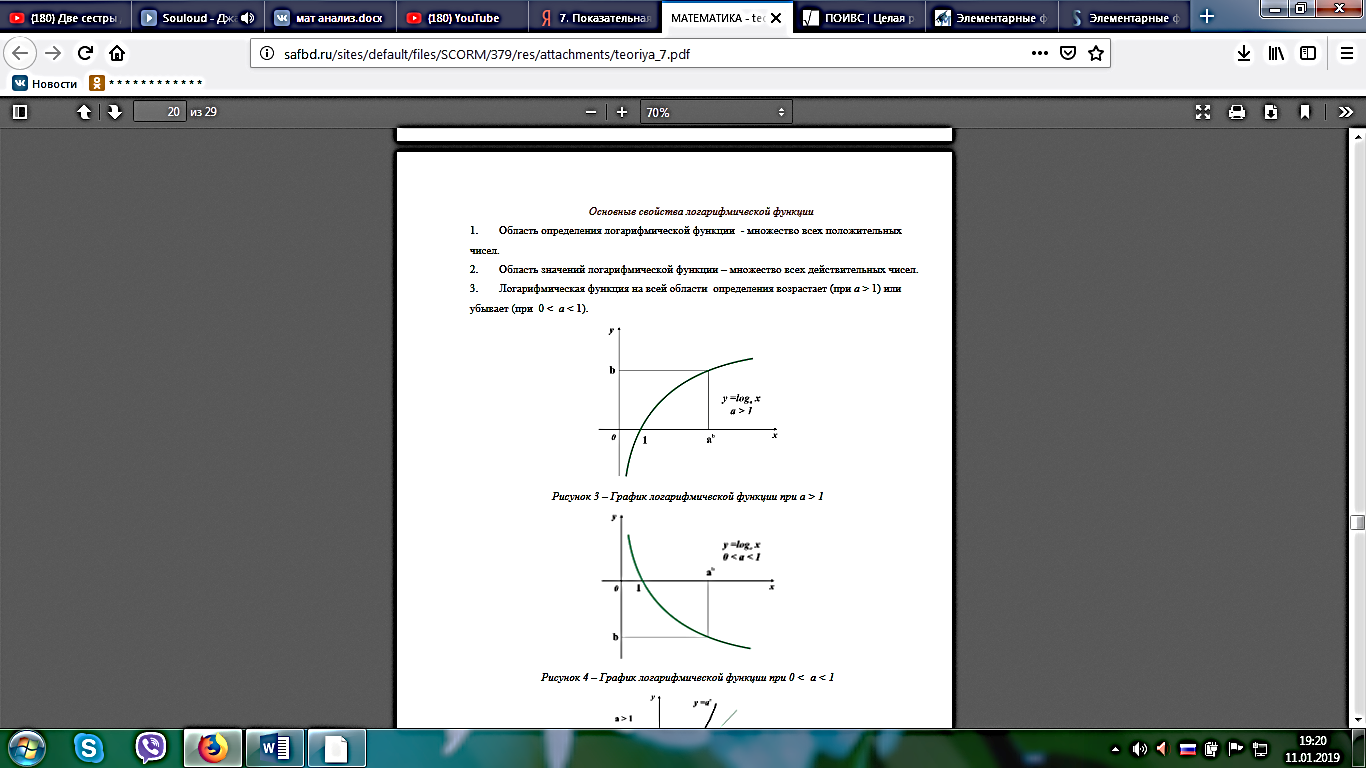

8. 
   Тригонометрические и обратные тригонометрические функции и их графики .
   

Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.

Функция арксинус y = arcsin(x).

Изобразим график функции арксинус: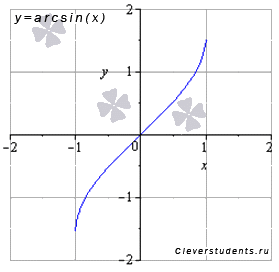



Свойства функции арксинус y = arcsin(x).

• 
  Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .
  
• 
  Область значений функции y = arcsin(x): .
  
• 
  Функция арксинус - нечетная, так как .
  
• 
  Функция y = arcsin(x) возрастает на всей области определения, то есть, при .
  
• 
  Функция вогнутая при , выпуклая при.
  
• 
  Точка перегиба (0; 0), она же ноль функции.
  
• 
  Асимптот нет.
  

Функция арккосинус y = arccos(x).

График функции арккосинус имеет вид: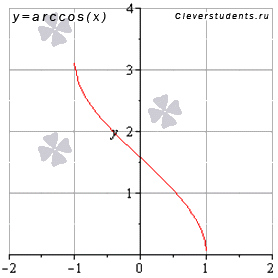



Свойства функции арккосинус y = arccos(x).

• 
  Область определения функции арккосинус: .
  
• 
  Область значений функции y = arccos(x): .
  
• 
  Функция не является ни четной ни нечетной, то есть, она общего вида.
  
• 
  Функция арккосинус убывает на всей области определения, то есть, при .
  
• 
  Функция вогнутая при , выпуклая при.
  
• 
  Точка перегиба .
  
• 
  Асимптот нет.
  

К началу страницы

Функция арктангенс y = arctg(x).

График функции арктангенс имеет вид: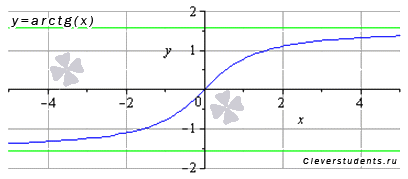



Свойства функции арктангенс y = arctg(x).

• 
  Область определения функции y = arctg(x): .
  
• 
  Область значений функции арктангенс: .
  
• 
  Функция арктангенс - нечетная, так как .
  
• 
  Функция возрастает на всей области определения, то есть, при .
  
• 
  Функция арктангенс вогнутая при , выпуклая при.
  
• 
  Точка перегиба (0; 0), она же ноль функции.
  
• 
  Горизонтальными асимптотами являются прямые приипри. На чертеже они показаны зеленым цветом.
  

К началу страницы

Функция арккотангенс y = arcctg(x).

Изобразим график функции арккотангенс: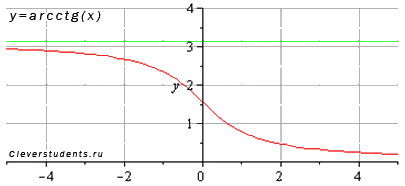



Свойства функции арккотангенс y = arcctg(x).

• 
  Областью определения функции арккотангенс является все множество действительных чисел: .
  
• 
  Область значений функции y = arcctg(x): .
  
• 
  Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
  
• 
  Функция убывает на всей области определения, то есть, при .
  
• 
  Функция вогнутая при , выпуклая при.
  
• 
  Точка перегиба .
  
• 
  Горизонтальными асимптотами являются прямые при(на чертеже показана зеленым цветом) и y = 0 при.
  

Арктангенс ( y = arctg x )  – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения    и множество значений  .
tg(arctg x) = x    
arctg(tg x) = x    

Арктангенс обозначается так:
.

График функции арктангенс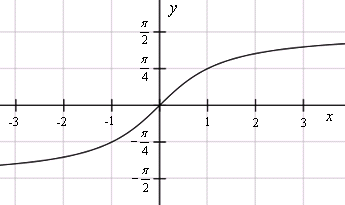



График функции   y = arctg x

График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом   , на котором функция монотонна. Такое определение называют главным значением арктангенса.

Арккотангенс, arcctg

Арккотангенс ( y = arcctg x )  – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения    и множество значений  .
ctg(arcctg x) = x    
arcctg(ctg x) = x    

Арккотангенс обозначается так:
.

График функции арккотангенс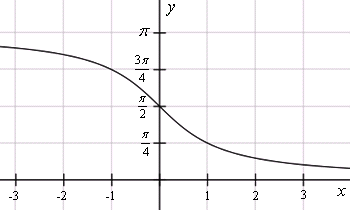



График функции   y = arcctg x

График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом   , на котором функция монотонна. Такое определение называют главным значением арккотангенса.

Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x

Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x.