конторольная работа по дискретной математике. Решение готовое Дискретная математика. Контрольная работа 1,2 По дисциплине Дискретная математика Иванов Н. А. Шифр кт20икт(БТ)004 Проверил Кожевникова Т. В
 Скачать 291.5 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования Дальневосточный государственный университет путей сообщения Кафедра: «Высшая математика» КОНТРОЛЬНАЯ РАБОТА №1,2 По дисциплине: «Дискретная математика» Выполнил: Иванов Н.А. Шифр: КТ20-ИКТ(БТ)004 Проверил: Кожевникова Т.В. Хабаровск, 2022 г. КОНТРОЛЬНАЯ РАБОТА №1 Задание 1. Для заданных множеств U = {2, 3, 4, 7}, A = {2, 3, 4}, B = {3, 4}, C = {2, 7} найдите мощность следующих множеств: 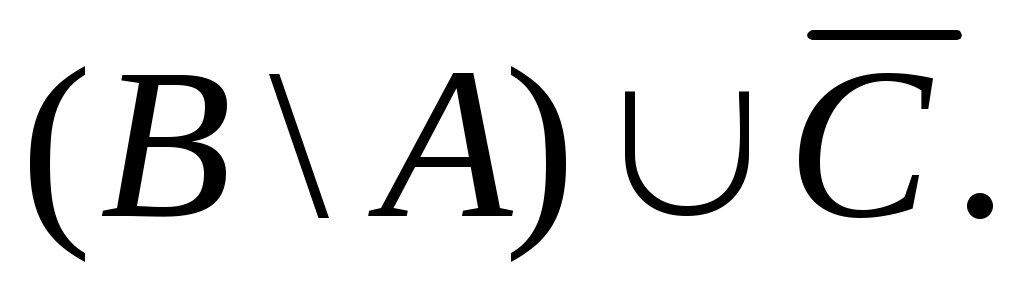    Решение 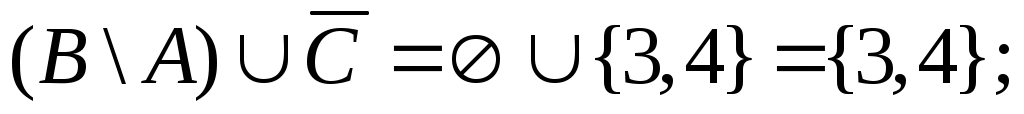 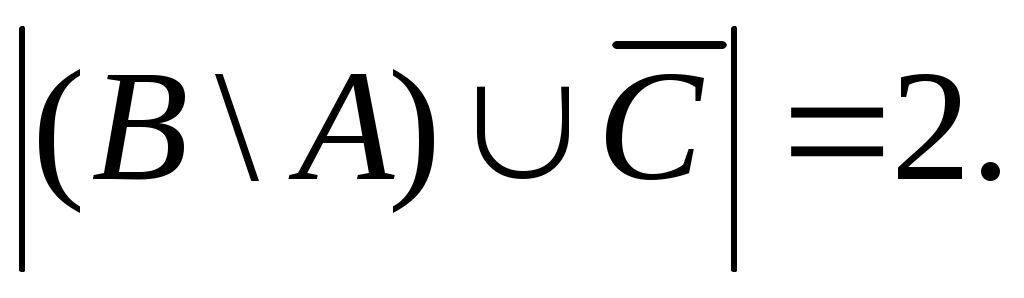       Задание 2. Даны два множества  и  . Укажите множество целых чисел, принадлежащих пересечению и объединению множеств А и В. Решение   Таким образом, пересечению множеств А и В принадлежат целые числа -3, -2, -1, 0. Объединению множеств А и В принадлежат целые числа -4, -3, -2, -1, 0, 1, 2, 3. Задание 3. С помощью диаграмм Эйлера – Венна изобразите множества и закрасьте ту часть, которая соответствует указанным операциям:  Решение 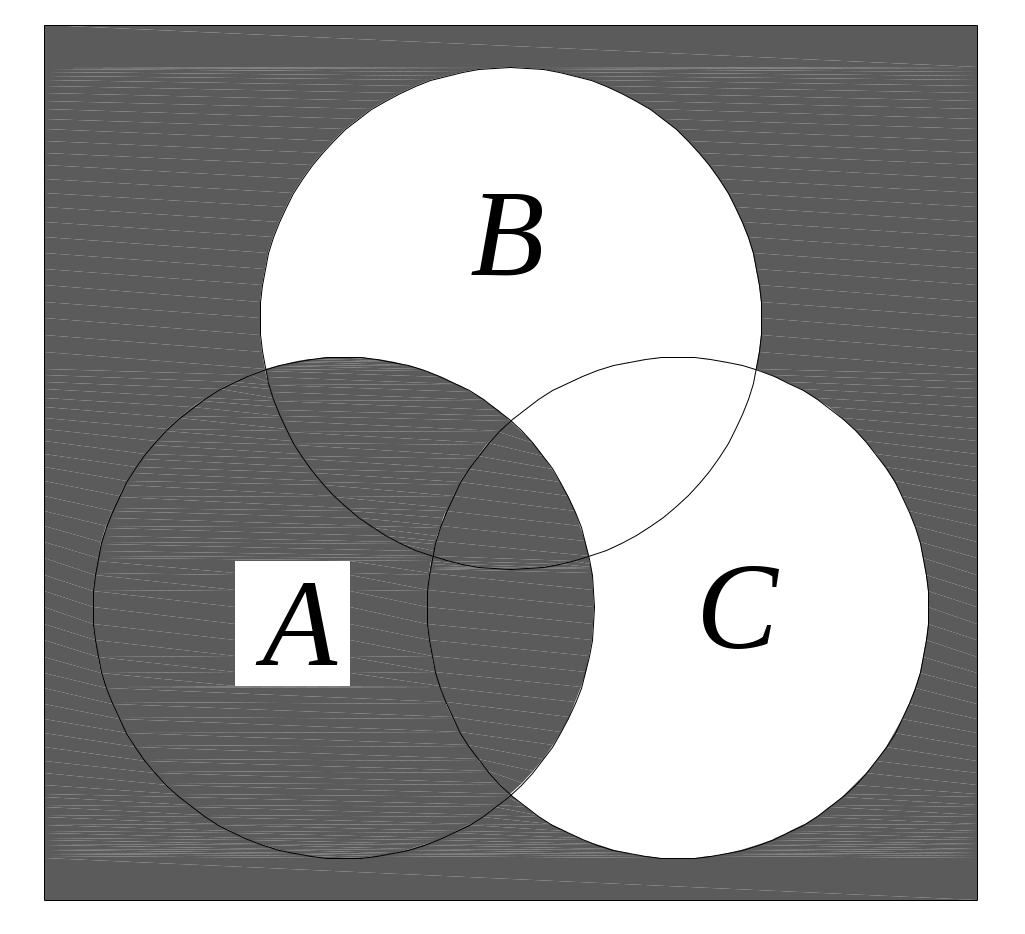 Задание 4. Найдите неизвестное x из уравнения  Решение Имеем: 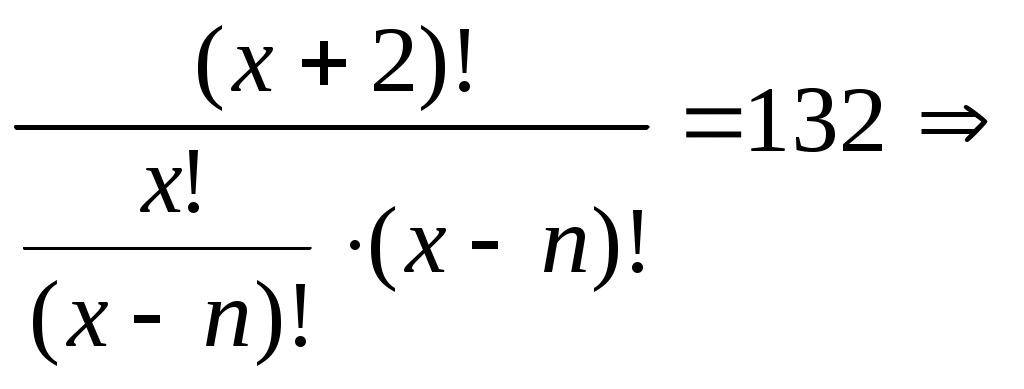    Поскольку среди корней только х = 10 является натуральным, то решение х = 10. Задание 5. Четыре автора должны написать книгу из 17 глав, причем первый и третий должны написать по пять глав, второй – 4, а третий – 3 главы книги. Сколькими способами можно распределить главы между авторами? Решение Первый автор может выбрать 5 глав из 17  способами.Второй автор может выбрать 4 главы из оставшихся 12  способами.Третий автор может выбрать 5 глав из оставшихся 18  способами.Общее число способов:  Задание 6. Даны множества A = {a, b, c, d}, B = {a, c, d, f}, C = {a, b, f, e}. Найти число элементов декартова произведения множеств  и указать эти элементы.Решение Имеем:  Тогда:   Задание 7. Пусть даны два множества:  . Изобразить в декартовой системе координат область, соответствующую декартовому произведению множеств  .Решение  Задание 8. Дано алгебраическое бинарное отношение  . Установить, какими свойствами обладает данное бинарное отношение. Решение а) Рефлексивность: для   отношение нерефлексивно, поскольку при  b) Симметричность:  и   отношение симметрично. c) Транзитивность: для  и  следует  отношение транзитивно.КОНТРОЛЬНАЯ РАБОТА №2 Задание 1. Дана матрица смежности 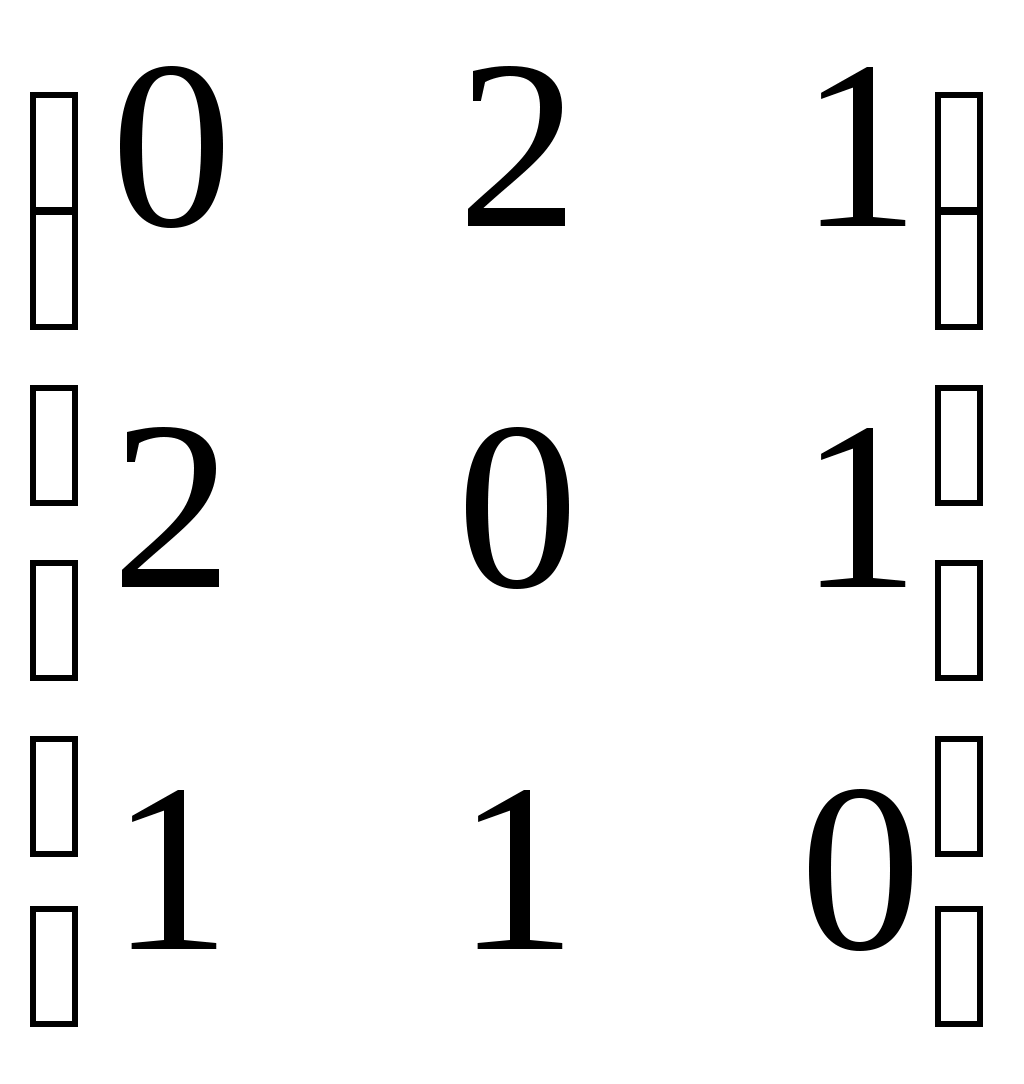 . Изобразить соответствующий размеченный граф.Решение 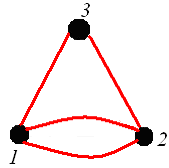 Задание 2. Даны графы G1 и G2. Выпишите для каждого графа множества вершин и ребер. Определите степень каждой вершины. Найдите матрицы смежности и инцидентности. Укажите для графа G1, какой-либо маршрут из вершины 1. Укажите для графа G2 подграфы. 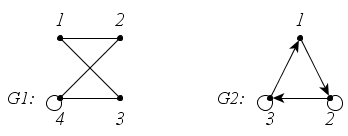 Решение Граф G1. Множество вершин: V = {1, 2, 3, 4}. Множество ребер: Е = {(1,2), (1,3), (2,4), (3,4), (4,4)}. deg(1) = 2; deg(2) = 2; deg(3) = 2; deg(4) = 4. Матрица смежности: 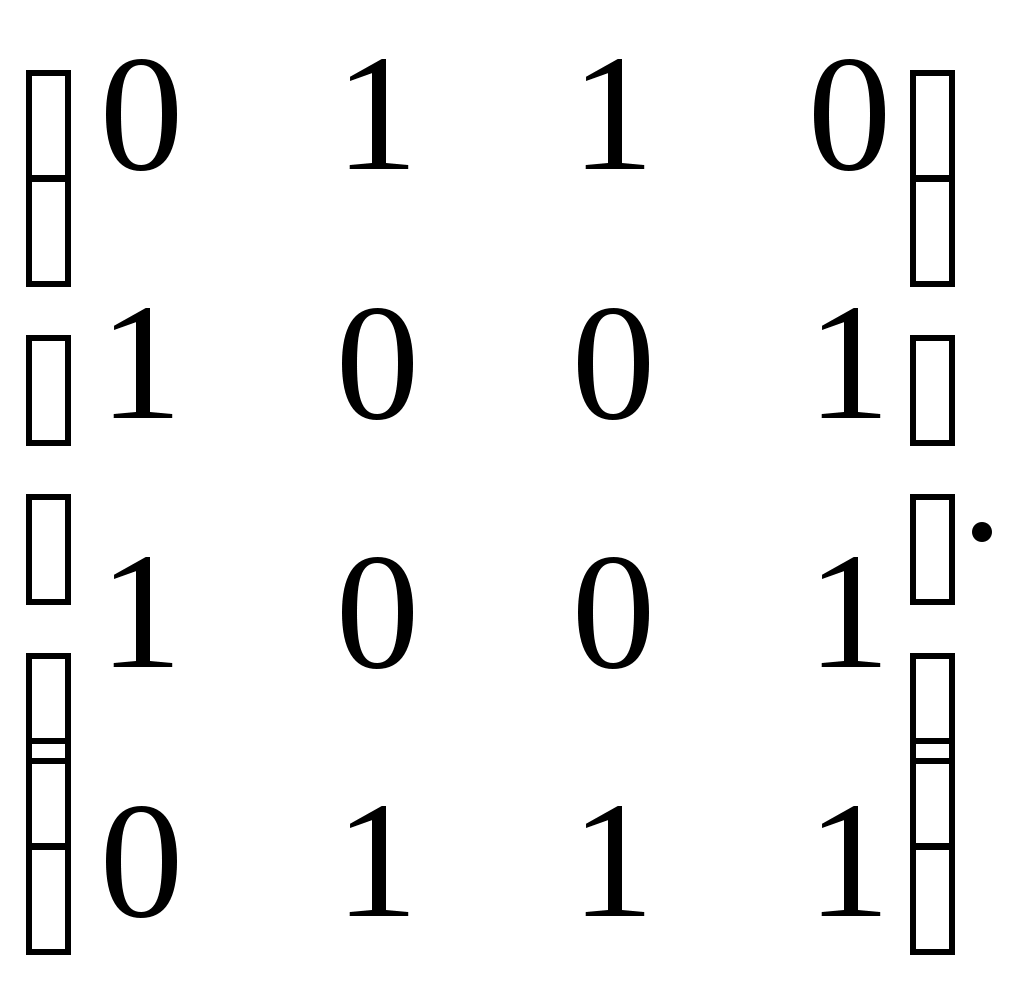 Матрица инцидентности: 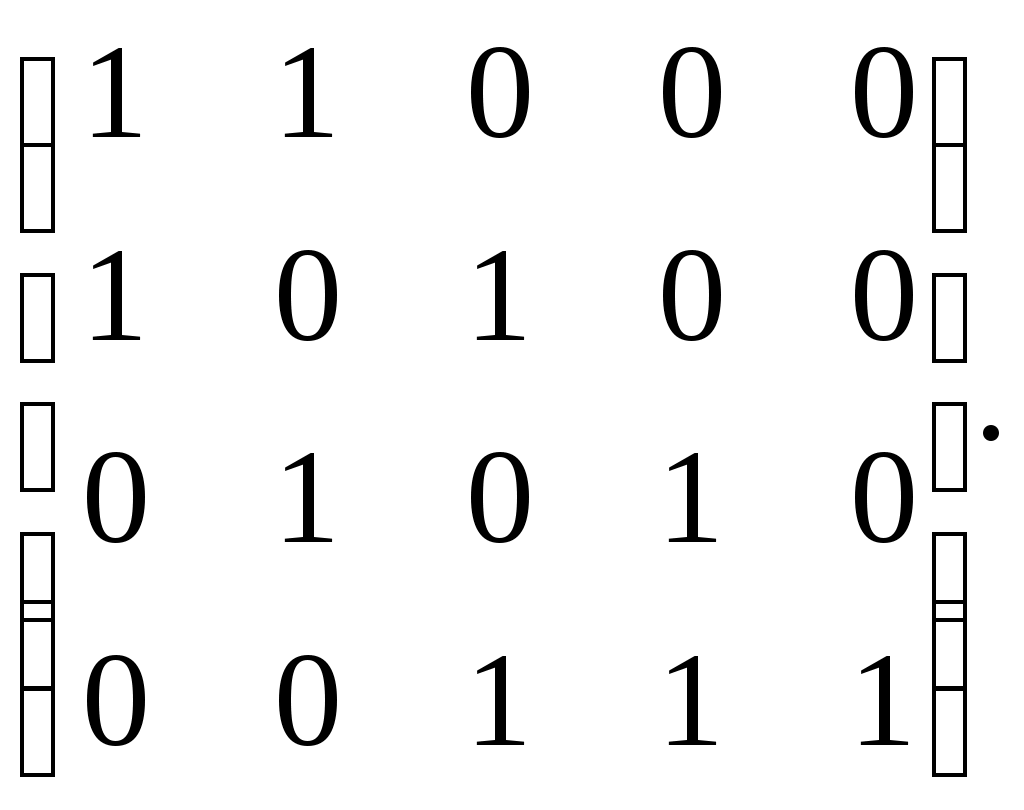 Маршрут из вершины 1 в вершину 4: 1, (1, 2), 2, (2, 4), 4. Граф G2. Множество вершин: V = {1, 2, 3}. Множество ребер: Е = {(1,2), (2,2), (2,3), (3,1), (3,3)}. deg(1) = 2; deg(2) = 4; deg(3) = 4. Матрица смежности: 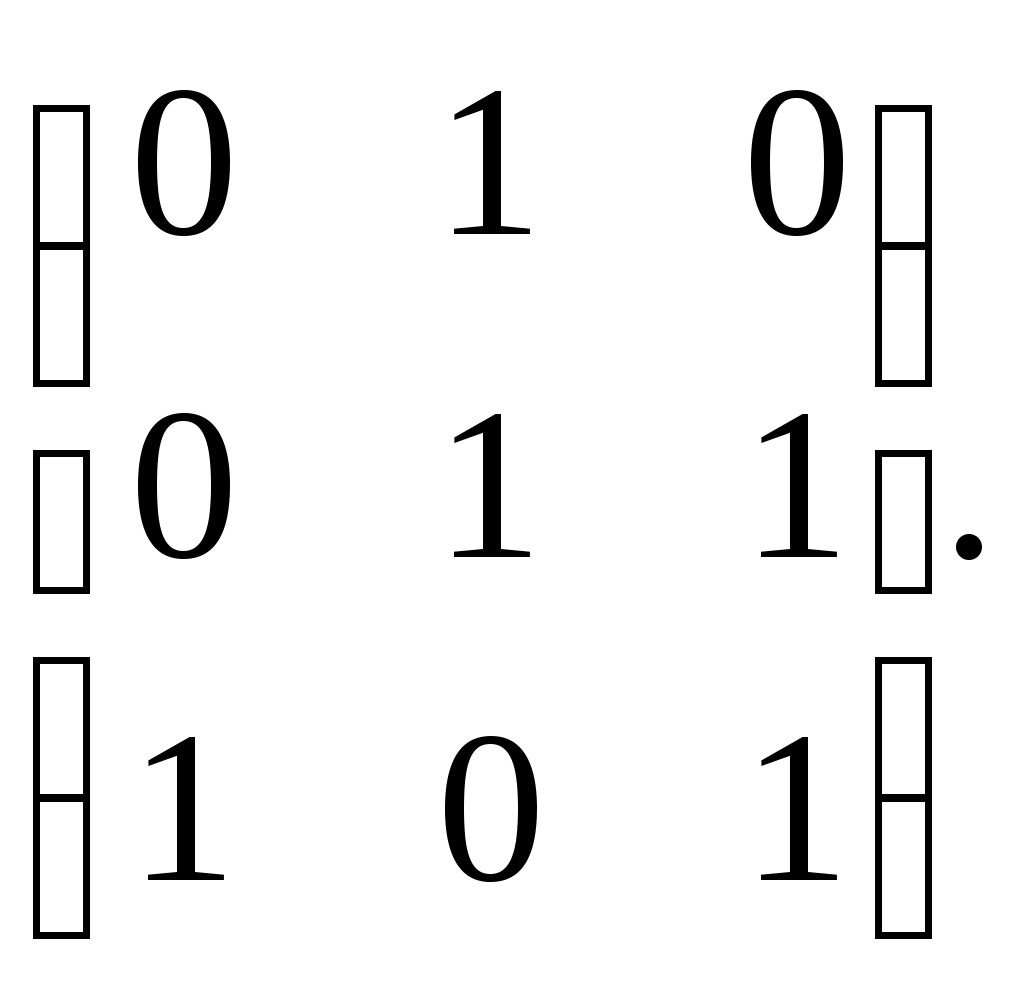 Матрица инцидентности: 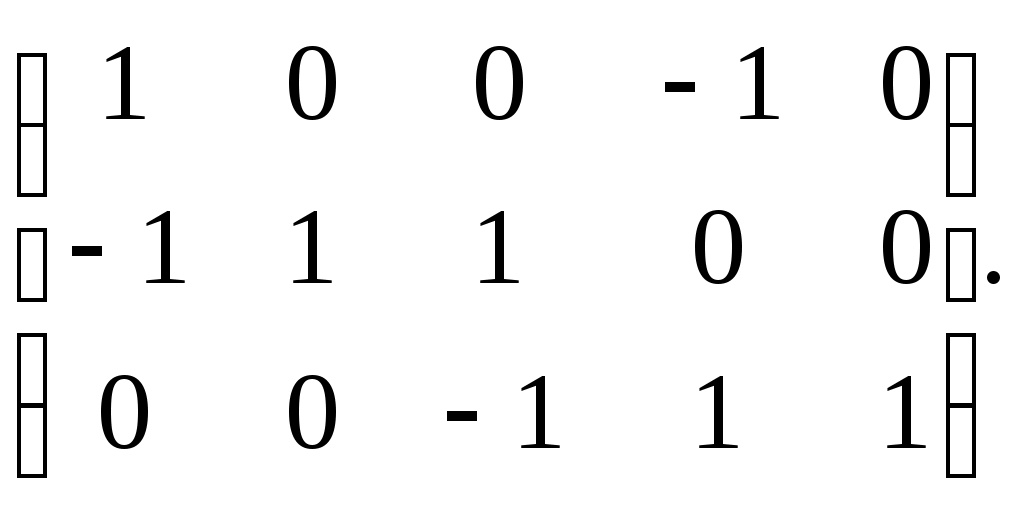 Подграфы графа G2 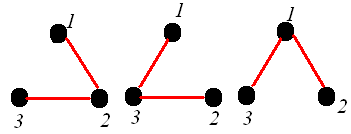 Задание 3. Постройте односторонне связный ориентированный граф на девяти вершинах. Найдите диаметр этого графа. Решение 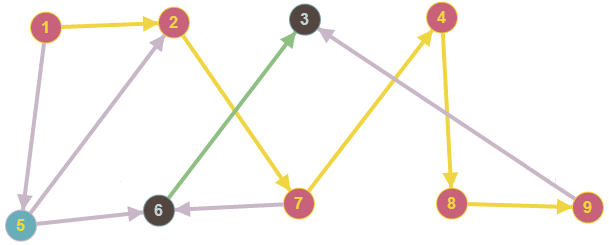 Диаметр графа: 5 (1→2→7→4→8→9). Задание 4. Найдите остовные деревья графа, представленного на рисунке, без учета веса ребер а) методом поиска в ширину; б) методом поиска в глубину. В качестве начальной вершины выберите вершину V4. 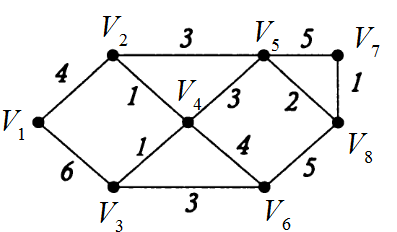 Решение а) метод поиска в ширину. 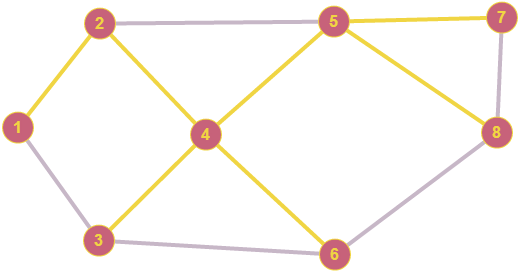 б) метод поиска в глубину 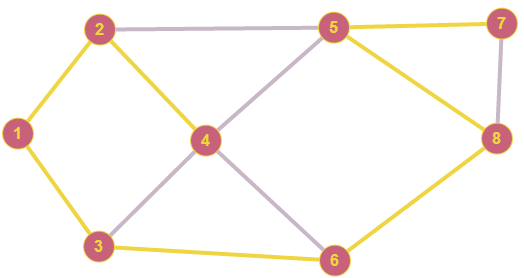 Задание 5. Для графа, представленного на рисунке, задайте весовую функцию ребер и постройте остовное дерево минимального веса, полагая, что ребра имеют различные положительные целые веса. Минимальный вес ребра равен 4. 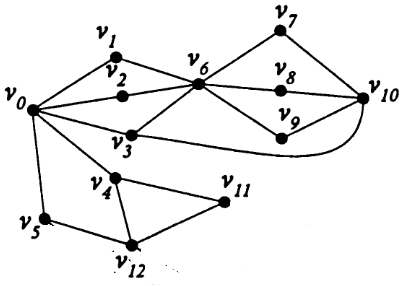 Решение 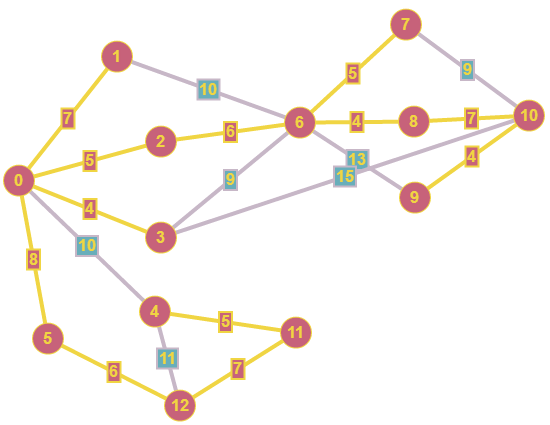 Вес минимального остовного дерева равен 68. |