Свойства степени с натуральным показателем».. Путешествие к замку Камелота 7 кл. Свойства степени с натуральным показателем
 Скачать 119 Kb. Скачать 119 Kb.
|
|
Конспект урока по алгебре в 7-м классе на тему: «Свойства степени с натуральным показателем». Цели урока: Образовательные: – отработка умений систематизировать, обобщать знания о степени с натуральным показателем, закрепить и усовершенствовать навыки простейших преобразований выражений, содержащих степени с натуральным показателем. Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога. Развивающие: - развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала. Тип урока: - обобщающий урок по теме. Вид урока:, комбинированный. Структура урока: 1. Организационный момент. 2. Мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений; сообщение темы, целей и задач урока. 3. Воспроизведение изученного и его применение в стандартных ситуациях. 4. Перенос приобретенных знаний, их первичное применение в новых или изменённых условиях, с целью формирования умений. 5.Элементы здорорвьесберегающих технологий. 6.Самостоятельное выполнение учащимися заданий под контролем учителя. 7.Подведение итогов урока и постановка домашнего задания. Ход урокаОрг. момент: Сегодня на уроке мы обобщим важную тему “Свойства степени с натуральным показателем”, которая позволит нам подходить к решению многих задач рационально, т.е. затрачивать на их выполнение минимум времени и выполнять их без ошибок. Вы увидите, как просто можно справиться с заданием, если запомнить некоторые правила действий со степенями. Такая работа всегда доставляет большое удовольствие. Находить красивые решения математических задач – одно из предназначений предмета “ МАТЕМАТИКА».(Слайд1.) Мы сегодня совершим путешествие к замку Камелота, в ходе которого обобщим знания и умения по теме: «Степень с натуральным показателем». 2. Тема урока.Эпиграф урока. (Слайд 2)«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов 3. Цели и задачи урока (Слайд 3). 4. Устно: Станция «Чемоданная». (Слайд 4-5) Собираемся в дорогу – складываем знания в чемодан. 1) Нужно устно ответить на вопросы: Сформулируйте определение степени числа с натуральным показателем Сформулируйте свойство умножения степеней с одинаковыми основаниями Сформулируйте свойство деления степеней с одинаковыми основаниями Сформулируйте свойство возведения степени в степень Сформулируйте свойство возведения дроби в степень Сформулируйте свойство возведения в степень произведения Итак, чемоданы собраны, отправляемся в путь. На нашем пути… 5. ОКЕАН УСТНЫХ ЗАДАЧ (Слайд 6) 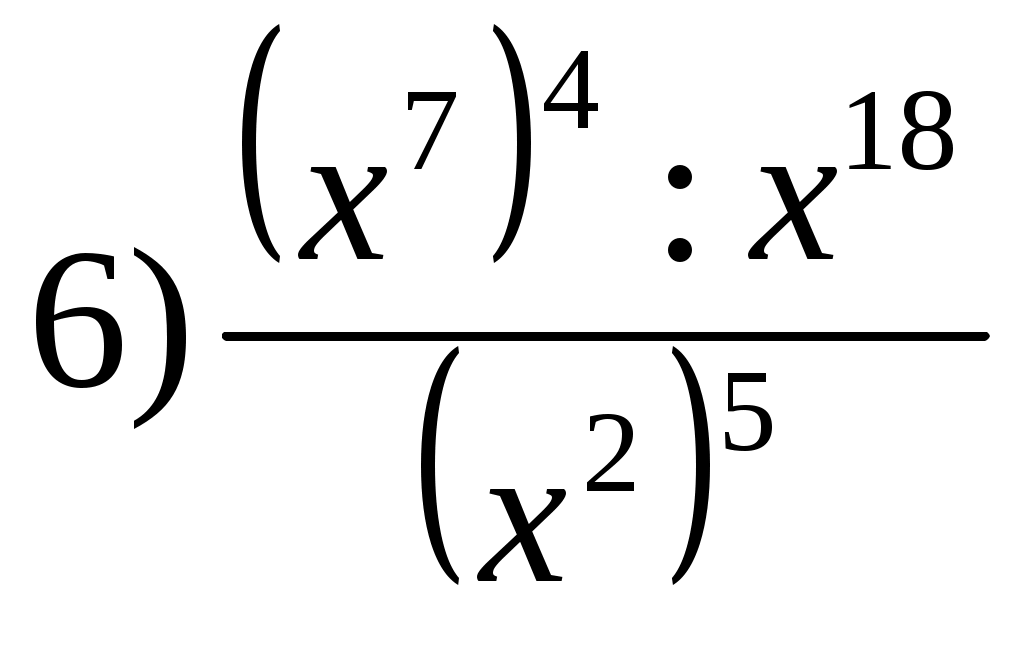 Молодцы! Вы успешно проплыли по океану Устных задач, но на нашем пути «Логово ошибок» 6. ЛОГОВО ОШИБОК (Слайд 7) Найдите и исправьте ошибки. 5 · 5 · 5 · 5 = 45 ( - 3)2 =- 9 23 · 27 =221 ( 2х )3 = 2х3 53 · 54 = 257 23 + 22 = 25 ( 3а)2 = 3а2 310 : 35 = 32 Внимание! Мы подходим к пустыне «Звездочетов». 7. Пустыня звездочетов. (Слайд 8) Работа в тетрадях. Какие выражения нужно поставить вместо (*), чтобы получить тождество: а12 · а* : а10 = а5 а · а* = а7 (а2)3 · * = а24 (а2 в)* = а10 в5 ( * в4)3 = 8а9 в12 Продолжаем наше путешествие и на нашем пути «Бухта удачи». 8. БУХТА УДАЧИ (Слайд 9) Работа в тетрадях и у доски.. Записать в виде степени с основанием а. 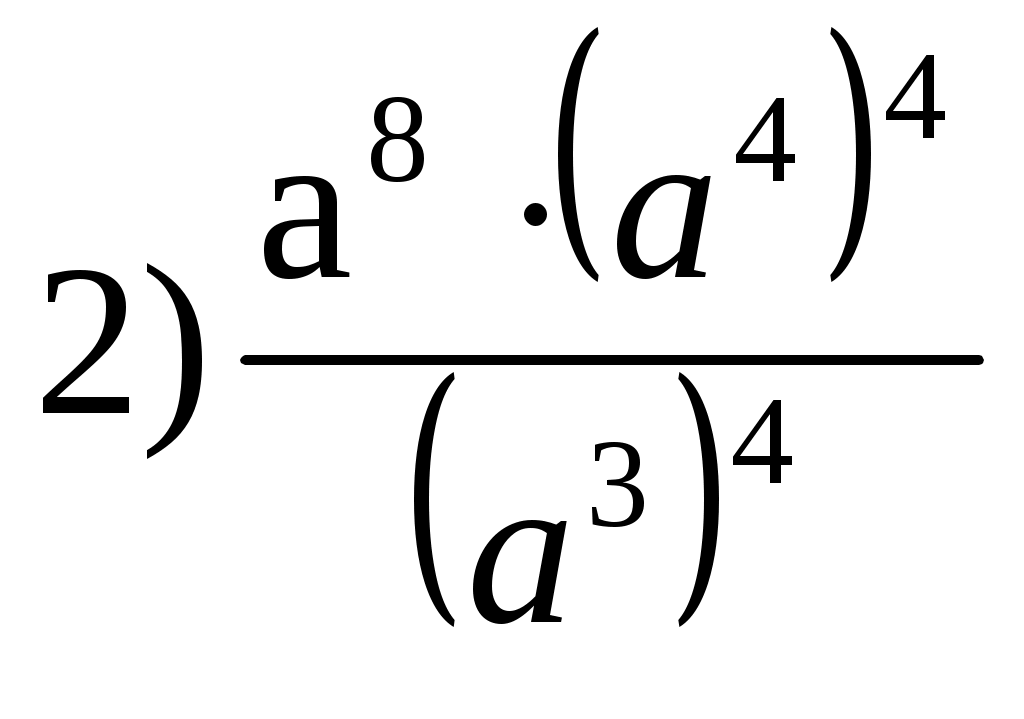 На выходе из бухты нас встречает замок «Таинственный». Давайте посетим его. 9. Замок Таинственный (Слайд 10) В тетрадях и у доски. Физкультминутка. (Слайд 11) Отдохнули? Попробуем преодолеть горы «Мозголомы». 11 (Слайд 12 - 13) Работа у доски и в тетрадях. 12. Бухта Историческая (Слайд 14 – 15) У древних вавилонян, египтян и китайцев имелись некоторые отдельные знаки – иероглифы для немногих математических понятий. Однако лишь в «Арифметике » Диофанта (3в) встречаются зачатки алгебраической буквенной символики Не любое число Диофант обозначал буквой, а только неизвестное и его степени. Неизвестное, названное «аритмос» (число), обозначалось s2, игравшим роль нашего «х». Особые обозначения имели вторая степень неизвестного, названная «динамос», т.е. «сила», третья степень «кубос», четвертая- «динамо-динамис», пятая -«динамо-кубос», шестая -«кубо-кубос» Подобно Диофанту европейские математики 16 века вторую степень неизвестного называли «сила», а также «квадрат» (Quadratus), третью степень- «куб» (Cubus). Виет применял сокращения: N для первой степени, Q-для второй, C-для третьей, QQ-для четвертой степени и т.д. например: 1C-8Q+16N aequatur 40 означает в сокращении х3-8х2+16х=40. М.Штифель писал ААА вместо А3; английский математик начала 17 века Т.Гарриот писал аааа вместо а4. Англичанин Оутред писал в 1531 году  и т.д. и т.д.Современная запись, вроде Х4, х5 была введена Декартом. 13. (Слайд 16) Продолжаем путешествие. Устно. 14. Уважаемые школьники! (Слайд 17) Вы были настойчивы и успешно достигли Камелота. В награду вам присваивается звание «ЮНЫХ МАТЕМАТИКОВ». Король АРТУР 15. МЫС НАДЕЖДЫ (Слайд 18) Самостоятельная работа. (У каждого на столе карточка с заданием)Вариант 1 Вариант 2 1) Выполните действие:
2) Вычислите значение выражения
16. Результаты урока:Подведение итогов урока, выставление оценок. (Слайд 19) Девочки и мальчики, вы активно участвовали в уроке, поэтому вы молодцы. Давайте ответим на вопросы: - Сегодня на уроке я повторил… - сегодня на уроке я закрепил… - сегодня на уроке я узнал… – Перечислите свойства степени с натуральным показателем. Оценки за урок поставим после проверки, самостоятельной работы, учитывая, ответы тех учащихся, которые отвечали в течение урока. 17. Домашнее задание. Что произошло с понятием степени в XVII веке, мы с вами можем предсказать сами. Для этого попробуйте ответить на вопрос: можно ли число возвести в отрицательную степень или дробную? (Дают свои версии). Но это предмет нашего будущего изучения. Домашнее задание. Обязательная часть: 1. Выполните действия: а) а 3а5; б) а10 : а7 ;в) (а2)4; г) (ав)5. 2. Найдите значение выражения: -х² + 3х при х = 5. 3. Вычислите: а) 1,254 84; б) 612 36*69 Дополнительная часть: 4. Упростите: (((-а)2)3)4. 5. Найдите значение выражения: а) (-0,2)0 – 0,23; б) 81*(1/3)4 – 0,05*(-10)2. |
