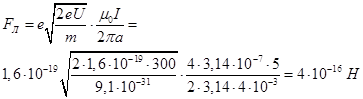Физика 2. Контрольная работа 2 по дисциплине Физика студент 3го курса, группы узкб18
 Скачать 229.04 Kb. Скачать 229.04 Kb.
|
 ИНСТИТУТ МЕЖДУНАРОДНОГО ОБРАЗОВАНИЯ КАФЕДРА УПРАВЛЕНИЯ КАЧЕСТВОМ И СТАНДАРТИЗАЦИИ КОНТРОЛЬНАЯ РАБОТА №2 по дисциплине «Физика» Выполнил: студент 3-го курса, группы УЗКБ-18 специальности «Управление качеством» Орлов Евгений Проверил преподаватель к.э.н доцент Донской А.Д_ Электромагнитизм. 17 Рамка, содержащая 1000 витков площадью 100 см 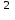 , равномерно вращается с частотой 10 с , равномерно вращается с частотой 10 с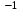 в магнитном поле напряженностью 10 в магнитном поле напряженностью 10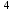 А/ м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную э.д.с. индукции, возникающую в рамке. А/ м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную э.д.с. индукции, возникающую в рамке.Решение. 100 см2 = 100∙10-4 м2 = 10-2 м2. Магнитная индукция и напряженность магнитного поля связаны соотношением: B=μ⋅μ0⋅H (1). Где: μ = 1, μ – магнитная проницаемость среды, μ0 – магнитная постоянная, μ0 = 4∙π∙10-7 Н/А2. Зависимость магнитного потока, пронизывающего рамку, от времени определяется по формуле Φ=B⋅S⋅cosα, Φ=B⋅S⋅cos(2⋅π⋅ν⋅t), Φ=μ⋅μ0⋅H⋅S⋅cos(2⋅π⋅ν⋅t) (2). Мгновенное значение ЭДС индукции определяется уравнением Фарадея – Максвелла E=−dΨdt(3),Ψ=N⋅Φ(4),E=−N⋅dΦdt,E=−N⋅d(μ⋅μ0⋅H⋅S⋅cos(2⋅π⋅ν⋅t))dt,E=N⋅μ⋅μ0⋅H⋅S⋅2⋅π⋅ν⋅sin(2⋅π⋅ν⋅t)(5),E=Emax⋅sin(2⋅π⋅ν⋅t)(6),Emax=N⋅μ⋅μ0⋅H⋅S⋅2⋅π⋅ν(7).Emax=1000⋅1⋅4⋅3,14⋅10−7⋅104⋅10−2⋅2⋅3,14⋅10=8203⋅10−5=0,082. Ψ – потокосцепление. Еmax = 0,082 В. 31 Уравнение изменения со временем тока в колебательном контуре имеет вид I=0,02 sin 400πt А. Индуктивность контура L=1 Гн. Найти период Т колебаний, емкость С контура, максимальную энергию магнитного поля и максимальную энергию электрического поля.
45. Электрон, ускоренный разностью потенциалов 300 В, движется параллельно прямолинейному длинному проводу на расстоянии 4 мм от него. Какая сила F действует на электрон, если по проводнику пустить ток 5 А?
Оптика. Нa поверхность дифракционной решетки нормально кее поверхностипадает монохроматический свет. Постоянная дифракционнойрешетки в n= 4,6 раза больше длины световой волны. Найти общее число дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.
Дано d=4,6ƛ 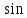 M-? Решение задачи: Условные главные при дифракции света на дифракционной решетке d * 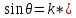 ƛ ƛd- период решетки k= 0,1,2 Так как d=4,6ƛ, то 4,6 * ƛ * 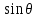 = ±k * ƛ . = ±k * ƛ .Поэтому k= 4,6 * 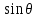 Максимальный порядок наблюдается при 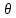 = =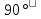 M= 4,6 * 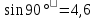 A так порядок – это целое число целочисленное, то М=4. Поэтому слева и справа о т центрального максимума будет по 4 максимума. Поэтому общее число максимумов равно 2*4+1=9 37. Поток излучения абсолютно чёрного тела равен 10 кВт, максимум энергии излучения приходится на длину волны 0,8 мкм. Определить площадь излучающей поверхности. Дано: Фe = 10 кВт = 1,0 • 104 Вт, λmax = 0,8 мкм = 0,8 • 10-6 м. Определить: S. Решение По закону смещения Вина длина волны λmax обратно пропорциональна температуре T черного тела: λmax = C’/T, где C’ = 2,898 • 10-3 м • К – постоянная Вина, откуда T = C’/λmax. (1) Энергетическая светимость Re равна отношению потока излучения Фe, испускаемого телом, к площади поверхности S и, согласно закону Стефана – Больцмана, пропорциональна четвертой степени температуры: Re = Фe/S = σT4, где σ = 5,67 • 10-8 Вт/(м2 • К4) – постоянная Стефана – Больцмана. Поэтому S = Фe/(σT4), или, учетом выражения (1), S = Фe/(σ(C’/λmax)4) = Фeλmax4/(σC’4), что после подстановки числовых значений дает S = 1,0 • 104 • (0,8 • 10-6)4/(5,67 • 10-8 • (2,898 • 10-3)4) ≈ 0,00102 (м2) ≈ 10 см2. Ответ: 10 см2. 45. На металлическую пластину направлен пучок ультрафиолетового излучения с длиной волны 0,25 мкм. Фототок прекращается при минимальной задерживающей разности потенциалов в 0,96 В. Определять работу выхода электронов из металла. Дано: 0.25 мкм2.5107 м, Umin 0.96 B Найти: A - ? Решение: Запишем закон Эйнштейна для фотоэффекта: 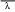 hc Ek max A. (1) hc Ek max A. (1)При приложении данной задерживающей разности потенциала Umin силы  E электрического будут совершать работу A еUmin по изменению  E кинетической энергии фотоэлектронов на величину Ek A еUmin Ek max . Следовательно, кинетическая энергия фотоэлектронов равна: Ek max е Umin . (2) Тогда (1) запишется в виде: 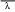 hc е Umin A. (3) hc е Umin A. (3)Отсюда определим работу выхода: 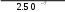  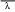 34 Ahc е Umin 6.63101 3108 1.61019 0.96 6.421019 Дж. (4) Ответ: работа выхода А электронов из металла равна: A6.421019 Дж Физика атома и атомного ядра. Основы квантовой механики. Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую, потенциальную и полную энергию электрона. Ответ выразить в электрон–вольтах. Дано: n 3 Найти: T,U,E – ? Решение: Получим выражения для кинетической, потенциальной и полной энергии электрона в атоме водорода. Согласно боровской теории атома момент импульса электрона в атоме равен: mr n, n 1,2,3.... (1) На основании второго закона Ньютона имеем: 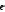  2 2 m r 40r2 . (2) Решая систему уравнений (1) и (2) относительно r и получим: 40 n2 me2 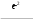 40n . 40n .Тогда кинетическая энергия для n 3 будет равна: Потенциальная:  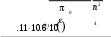 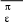  . U 4e20r 16me 2 1 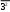   12 1698.851011.051034 2 1 4.8651019 Дж 3.041эВ 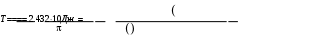 m2 me4 1 9.111031 1.61019 4 1 19 m2 me4 1 9.111031 1.61019 4 1 192 320 2 n2 32 8.851012 1.051034 2 32 , 1.52 эВ Потенциальная:  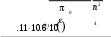 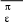  . U 4e20r 16me 2 1 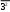   12 1698.851011.051034 2 1 4.8651019 Дж 3.041эВ И полная энергия равна:   E T U 32me 2 1 16me 2 1 32me4 2 1 E T U 32me 2 1 16me 2 1 32me4 2 1 T 2.4321019 Дж 1.52 эВ Ответ Числовые значения кинетической потенциальной и полной энергии электрона на второй боровской орбите равна T =1.52 эВ, U = -3.041эВ Дж, E = -1.52 эВ . 15. Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислить длину волны де Бройля для такого электрона. Дано Ek= (2m0c2) λ =? Решение Связь длины волны де Бройля с кинетической энергией Ek в классическом приближении λ= 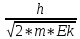 . . В релятивистском случае длину волны нужно вычислить по формуле λ= 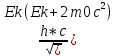 , , где 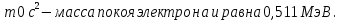 Но в этом случаи Ek = (2m0c2) больше энергии покоя электрона и поэтому нужно использовать релятивистскую формулу. Подставляем числа h= 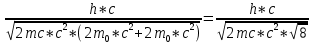 Подставляем числа h= 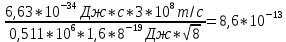 м м |