Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
ОТЧЕТ
Контрольная работа № 2
по дисциплине «Математическая логика и теория алгоритмов»
вариант №5
Выполнил:
Огнев Д. В.
Проверил:
____________________
1. Проверить, что A Δ B = C ⇔ B Δ C =A ⇔ C Δ A = B.
Сначала следует попробовать опровергнуть это утверждение, т. е. найти такие множества A, B и C, чтобы выполнялось отношение A Δ B = C, но не выполнялось A =B Δ C, или, наоборот, выполнялось A =B Δ C и не выполнялось A ΔB = C. После безуспешных попыток найти такие множества следует доказать данное утверждение.
Доказательство распадается на два этапа.
1. Докажем сначала, что AΔB =C ⇔ A =B Δ C. Таким образом, пусть A Δ B = C выполнено, докажем, что A =B Δ C. Поскольку требуется доказать включение множеств, то возьмем произвольный элемент x ∈ A и убедимся, что x ∈B Δ C. Элемент x может принадлежать B и может не принадлежать B. Если x ∈ B, то x ∈ A ΔB. Так как дано, что A Δ B = C, то получаем x ∈ C и, тем более, x ∈ B Δ C. Теперь рассмотрим случай, когда x ∉ B, тогда x ∈B и, тем более, x ∈B ∪ C.
2. Докажем теперь, что A = B Δ C ⇔A Δ B = C. Таким образом, пусть A =B Δ C выполнено, докажем, что A Δ B = C. Поскольку требуется доказать включение множеств, то возьмем произвольный элемент x ∈ A Δ B и убедимся, что x ∈ C. Имеем, если x ∈ A Δ B, то x ∈ A и, по условию, x ∈ B Δ C. Так как одновременно x ∈ B, то x ∉¬B и, следовательно, x ∈ C. Доказательство закончено.
2. Формула (p ⊃ q) & (q ⊃ r) & ¬ (p ⊃ r) — тавтология, противоречие или не то и не другое?
Доказательство. Пусть < p, q > = < p, r > ⇔ {{ p }, { p, q }} = {{ q }, { q, r }} ⇔ множества должны быть поэлементно равны и равенство возможно только в ситуации { p } = { q } и { p, q } = { r, p } ⇔ p = p и { p, q } = { r, q } ⇔ p = r и q = r.
3. Переведите с естественного языка на язык логики предикатов: Синус и косинус равны друг другу тогда и только тогда, когда равны тангенс и котангенс.
M = {функции}. Предикаты: D(x) ≡ «x — sin», C(x) ≡ «x —
cos », Т (x) ≡ «x — tg», С (x) ≡ «x — сtg»,
Формула: ∀x (D(x) = C(x)) ( Т (x) = С (x))
4. Переведите с естественного языка на язык логики предикатов: Не все решения уравнения sin 5x = 0 иррациональны
Решение: если задачу может решить не математик, то может решить и математик
5. Найдите отношения ρ–1, ρ ° ρ , ρ–1 ° ρ–1 для бинарного отношения x ρ y ⇔ «x2 + y2 = 1», определенного на множестве Z целых чисел.
Решение: ρ2 совпадает с ρ, поскольку любая пара элементов из Z , принадлежащая ρ, будет принадлежать и ρ2. Например, ∀x ∈ X xρx ⇒ xρ2x, кроме того xρy ⇒ yρy, а, значит xρ2y. Поэтому ρ2 как и ρ рефлексивно,симметрично, транзитивно.
6. На множестве {2, 0, 4} × {2, 0, 4} задано отношение R, определяемое следующим образом: 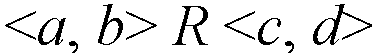 , если a – b = c – d. , если a – b = c – d.
а) Показать, что R есть отношение эквивалентности.
б) Описать классы эквивалентности.
Граф если R есть отношение эквивалентности:
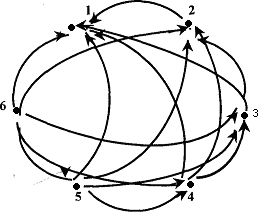
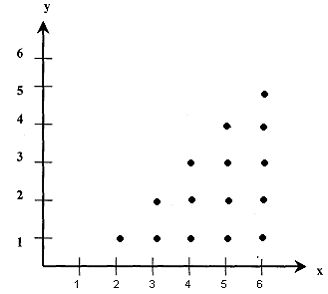
Строим график этого отношения:
Рефлексивность. Если бы это отношение было рефлексивным, то x > x для 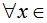 А. Например, было бы верно 2 > 2 (ложь ). Значит отношение «>» на А не является рефлексивным. А. Например, было бы верно 2 > 2 (ложь ). Значит отношение «>» на А не является рефлексивным.
Симметричность. Если бы это отношение было симметричным на множестве А, то x > у => у > х. Например, 3 > 2 => 2 > 3(ложь). Значит, отношение « > » на А не является симметричным.
Транзитивность. Если бы это отношение было транзитивным на множестве А, то x > у, у > z => x > z. Это утверждение истинно для любых натуральных чисел, т. е. и чисел из А. Значит, отношение « > » на А является транзитивным.
Асимметричность: Ни для каких чисел A не может быть одновременно истинным 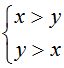 , т. е. отношение «>» на A асимметрично. Отношение « > » на множестве A является отношением строгого порядка, т. к. оно асимметрично и транзитивно. , т. е. отношение «>» на A асимметрично. Отношение « > » на множестве A является отношением строгого порядка, т. к. оно асимметрично и транзитивно.
7. Используя математическую индукцию, докажите для целого n ≥ 0, что 8n+2 + 92n+1 делится на 73
Предположим, что n = 0справедливо найдем 80+2+92*0+1= 145, т.е. 146/73 = 1,98 верно.
Предположим, что n = 1 справедливо найдем 81+2+92*1+1= 1241, т.е. 146/73 = 17 верно.
Таким образом мы доказали, что изменение всегда делится на 73.
8. Расположите следующие 5 функций в порядке увеличения скорости роста (каждая функция есть O (следующая)): 106 ln (ln n), 1010, n2, 4ln n /200, n3
1. 4ln n /200
2. 106 ln (ln n)
3. n2;
4. 1010;
5. n3.
2017
|
 Скачать 45.46 Kb.
Скачать 45.46 Kb.