Попов НС. Контрольная работа №2. Контрольная работа 2 по математике Вариант3 студент гр з512П81 Попов Николай Сергеевич нсо, снт Заря д. 164
 Скачать 3.4 Mb. Скачать 3.4 Mb.
|
|
Министерство образования РФ. Томский Государственный Университет Систем управления и радиоэлектроники (ТУСУР) Контрольная работа № 2 по математикеВариант№3 Выполнил: студент гр з-512П8-1 Попов Николай СергеевичНСО, снт Заря д. 164 630554 Проверил: кандидат физико - механических наук, доцент кафедры математики Васильева Оксана Владимировна Томск 2023 г Задание№1. Записать общее уравнение прямой, проходящей через точку М(-2; 4) перпендикулярно прямой x+2y+5=0. Найти площадь треугольника, образованную данной прямой и осями координат. Решение: Запишем уравнение прямой x+2y+5=0 в виде 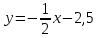 , , 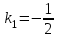 Прямая, перпендикулярная ей имеет угловой коэффициент 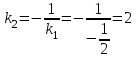 Ищем уравнение новой прямой: 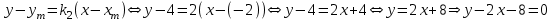 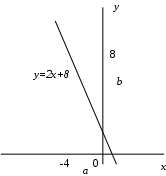 Площадь треугольника, образованного данной прямой и осями координат 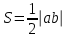 , где , где 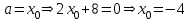 - отрезок, отсекаемый на оси OX; - отрезок, отсекаемый на оси OX;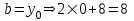 - отрезок, отсекаемый на оси OY; - отрезок, отсекаемый на оси OY;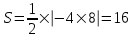 (кв.ед). (кв.ед).Ответ: 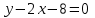 ; ; 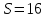 (кв.ед.) (кв.ед.)Задание№2. Записать общее уравнение прямой, проходящей через точку М(-2; 2)и отсекающей от первого координатного угла треугольник площадью S=4,5 кв.ед. Решение: 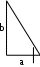 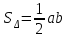 (1) (1)Уравнение прямой в отрезках : 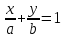 (2) (2)С учетом данных, подставив в (1) значение S, а в (2) значения координат точки M, получим систему уравнений, относительно aи b. 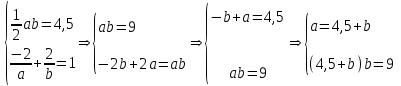 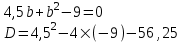 По условию задачи, прямая распологается в первом координатном углу, следовательно, принимаем 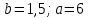 Уравнение прямой: 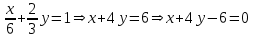 Ответ: 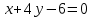 - общее уравнение прямой. - общее уравнение прямой.Задание№3. Даны вершины треугольника А(2, 1, 0), В(3, -1, 1) и С(1, 2, -4). Записать общее уравнение плоскости, проходящей через сторону АВ перпендикулярно плоскости треугольника АВС. Решение: Составляем уравнение плоскости, проходящей через плоскость треугольника: 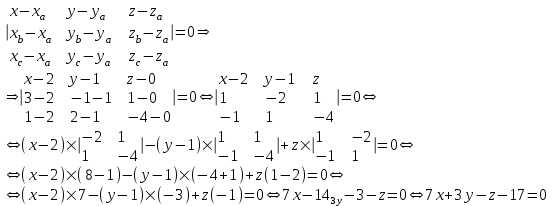 Составляем уравнение прямой АВ: 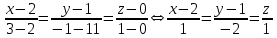 , , Составляем уравнение плоскости, проходящей через сторону АВ и перпендикулярно плоскости АВС: 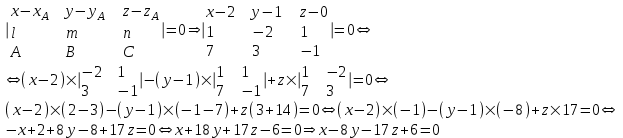 Ответ: 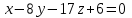 - общее уравнение плоскости, проходящей через сторону АВ перпендикулярно к плоскости треугольника АВС. - общее уравнение плоскости, проходящей через сторону АВ перпендикулярно к плоскости треугольника АВС. Задание№4 Найти расстояние от точки Р(1, 2, 0) до прямой 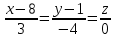 Решение: Расстояние от точки до прямой в пространстве определяется по формуле: 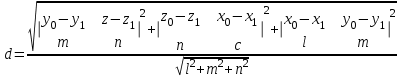 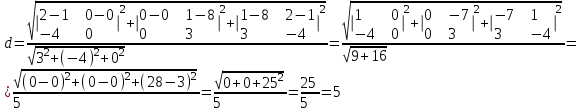 Ответ: d=5 Задание№5 Найти длину отрезка, отсекаемого от оси ординат плоскостью, которая проходит через точку А(1, 1, 6), перпендикулярно вектору АВ, где В – точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат с плоскостью 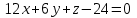 Решение: Находим вершины треугольника с осью OX: y=0; z=0; 12x-24=0 => x=2 C (2; 0; 0) с осью OY: x=0; z=0; 6y-24=0 => y=4 D (0; 4; 0) с осью OZ: x=0; y=0; z-24=0 =>z=24 E (0; 0; 24) Находим уравнения медиан этого треугольника , чтобы найти координаты точки В. Точка F – середина стороны, противоположная вершине С. 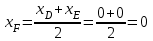   Точка F(0; 2; 12) – середина отрезка DE. Ищем середину отрезка CD – точку G.  ; ;  ; ;  Точка G(1; 2; 0). Координаты середины CE – точка K.  ; ;  ; ;  Точка K(1; 0; 12). Уравнение медиан: CF: 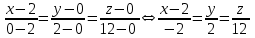 ; ;DK: 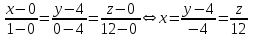 ; ;EG: 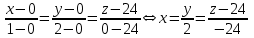 Точка пересечения медиан: 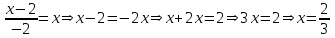 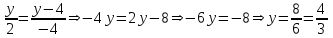 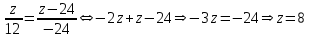 Можно взять любую пару уравнений медиан, таким образом точка пересечения медиан 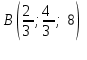 Координаты вектора 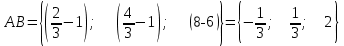 Ищем уравнение плоскости, проходящей через точку А перпендикулярно вектору АВ:  , получим: , получим: Длина отрезка, отсекаемого этой плоскостью от оси ординат:  Ответ:  Задание№6 Две прямые параллельны плоскости 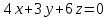 Первая прямая проходит через точку P(1, 2, 3) и пересекает ось абсцисс, а вторая – проходит через точку Q(3, 0, 0) и пересекает ось ординат. Найти косинус острого угла между направляющими векторами этих прямых. Первая прямая проходит через точку P(1, 2, 3) и пересекает ось абсцисс, а вторая – проходит через точку Q(3, 0, 0) и пересекает ось ординат. Найти косинус острого угла между направляющими векторами этих прямых. Решение: Косинус угла между прямыми: 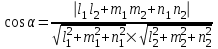 (1) (1)Условие параллельности прямой и плоскости: 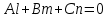 (2) (2)Каноническое уравнение для первой прямой (используем точки Р и (x0, 0, 0): 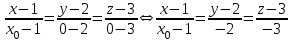 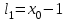 ; ; 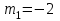 ; ; 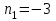 Чтобы найти 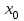 воспользуемся (2) воспользуемся (2)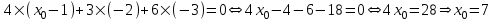 , тогда , тогда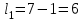 Каноническое уравнение для второй прямой (используем точки Q и (0, y0, 0): 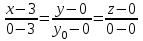 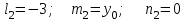 Чтобы найти 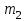 воспользуемся (2): воспользуемся (2): 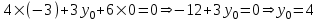 , тогда , тогда 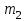 =4 =4Найденные значения направляющих коэффицентов подставляем в (1): 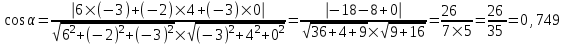 Ответ: 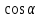 = 0,749 = 0,749Задание№7 Найти координаты центра С(x0, y0) окружности радиусом 5, касающейся прямой 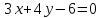 в точке М(2, 0), если известно, что точка С расположена в первой четверти. в точке М(2, 0), если известно, что точка С расположена в первой четверти.Решение: 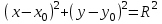 Точка С 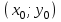 лежит на перпендикуляре к прямой лежит на перпендикуляре к прямой 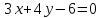 , так как эта прямая является касательной. , так как эта прямая является касательной.Предварительно перепишем уравнение заданной прямой в каноническом виде: 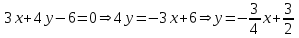 Тогда уравнение перпендикуляра: 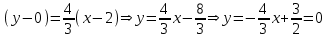 Расстояние от точки 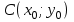 до прямой до прямой 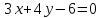 : :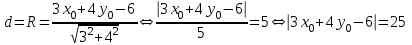 Получим систему уравнений относительно 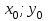 : :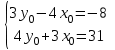 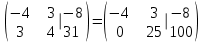 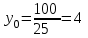 ; ; 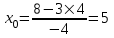 Ответ: 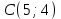 Задание№8 Дана кривая 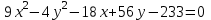 Доказать, что эта кривая – гипербола. Найти координаты ее центра симметрии. Найти действительную и мнимую полуоси. Записать уравнение фокальной оси. Построить данную гиперболу. Решение: 1. 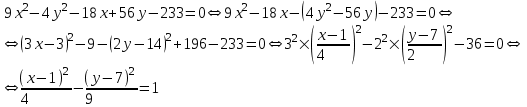 Положим 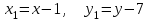 , тогда , тогда 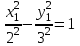 Данная кривая – гипербола. 2. Координаты центра:  Центр гиперболы: С(1; 7) 3. Действительная полуось a =2; мнимая полуось b=3. 4. Фокальные оси  5. Построение гиперболы: а). Отмечаем центр гиперболы. б). Отмечаем полуоси. в). На основе полуосей строим прямоугольник. г). Асимптоты проходят через диагонали этого прямоугольника.   Задание№9 Дана кривая 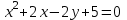 Доказать, что данная кривая – парабола. Найти координаты ее вершины. Найти значение ее параметра p. Записать уравнение ее оси симметрии. Построить данную параболу. Решение: 1. 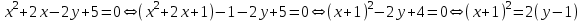 Введем замену 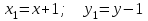 , получим , получим 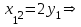 это каноническое уравнение параболы вида это каноническое уравнение параболы вида  , здесь , здесь  2. Координаты вершины параболы:  Точка А(-1; 2) – вершина параболы. 3. Параметр параболы: р = 1 4. Ось симметрии:  5. Построение: а). отмечаем вершину; б). ветви параболы направлены вверх.  Задание№10 Дана кривая  Доказать, что эта кривая – эллипс. Найти координаты центра его симметрии. 3. Найти его большую и малую полуоси. 4. Записать общее уравнение фокальной оси. 5. Построить данную кривую. Решение: Квадратичная форма  Приводим ее к главным осям; ее матрица  ; ;Записываем характеристическое уравнение этой матрицы: 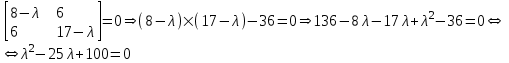 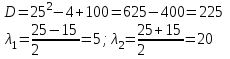 Корни 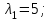 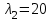 являются собственными числами. являются собственными числами.Так как 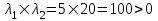 , то кривая , то кривая 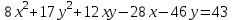 является являетсяэллипсом. Для 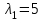 новый базисный вектор новый базисный вектор 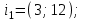 для для 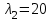 базисный вектор базисный вектор 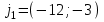 Записываем матрицу Q перехода от базиса 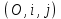 к к 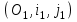 : : , ,  Выражаем новые координаты  и и  через старые: через старые: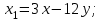 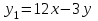 Записываем исходное уравнение в новой системе координат: 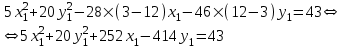 Выделяем полные квадраты: 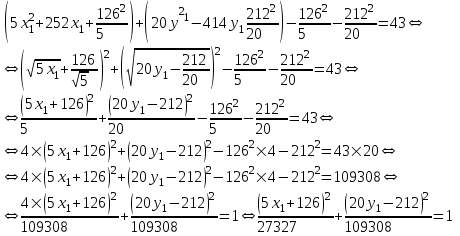  Перейдем к новой системе координат 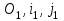 по формулам: по формулам: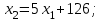 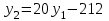 Получим: 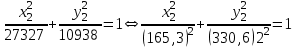  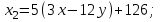 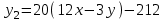 Решаем систему: 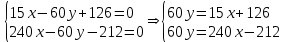 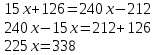 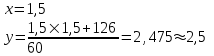 Нвое начало 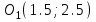 Новые оси направлены по прямым 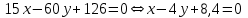 (ось (ось 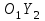 ) и ) и  (ось (ось  ) ) - большая полуось; - большая полуось; - малая полуось. - малая полуось.  |
