Контрольная работа 2 по теме Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов
 Скачать 21.4 Kb. Скачать 21.4 Kb.
|
|
Контрольная работа №2 по теме «Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов» Вариант 1 Найдите значение выражения: 3,5 ⋅ 23 − 34. Представьте в виде степени выражение: 1) x6⋅x8; 2) x8 : x6; 3) (x6) 8 ; 4) 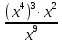 . .Преобразуйте выражение в одночлен стандартного вида: 1) −6a4b5⋅ 5b2⋅a6; 2) (−6m3n2) 3. Представьте в виде многочлена стандартного вида выражение: (6x2 − 5x + 9) − (3x2 + x − 7). Вычислите: 1) 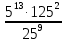 ; 2) ; 2) 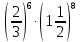 . .Упростите выражение: 128 x2y3 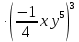 Вместо звёздочки запишите такой многочлен, чтобы образовалосьтождество: (4x2 − 2xy + y2) − (*) = 3x2 + 2xy. Докажите, что значение выражения (11n + 39) − (4n + 11) кратно 7 при любом натуральном значении n. Известно, что 6ab5 = −7. Найдите значение выражения: 1) 18ab5; 2) 6a2b10. Вариант 2 Найдите значение выражения 1,5 ⋅ 24 – 32. Представьте в виде степени выражение: 1) a4⋅a7; 2) a7 : a4; 3) (a7) 4 ; 4) 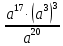 . .Преобразуйте выражение в одночлен стандартного вида: 1) −3x3y4x5⋅ 4y3; 2) (−4a6b) 3. Представьте в виде многочлена стандартного вида выражение: (5a2 − 2a − 3) − (2a2 + 2a − 5). Вычислите: 1) 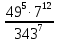 ; 2) ; 2)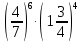 . .Упростите выражение: 81 x5y 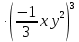 . .Вместо звёздочки запишите такой многочлен, чтобы образовалосьтождество: (5x2 − 3xy − y2) − (*) = x2 + 3xy. Докажите, что значение выражения (14n + 19) − (8n − 5) кратно 6 при любом натуральном значении n. Известно, что 4a3b = −5. Найдите значение выражения: 1) −8a3b; 2) 4a6b2. Вариант 3 Найдите значение выражения 33 - 2,5 ⋅ 25 . Представьте в виде степени выражение: 1) y9⋅y6; 2) y9 : y6; 3) (y6)9 ; 4) 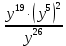 . . Преобразуйте выражение в одночлен стандартного вида: 1) −5m4n7⋅ 2m3n; 2) (−4a5b) 2. Представьте в виде многочлена стандартного вида выражение: (9y2 − 5y + 7) − (3y2 + 2y − 1). Вычислите: 1) 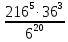 ; 2) ; 2)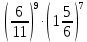 . .Упростите выражение: 125 x5y4 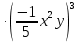 . .Вместо звёздочки запишите такой многочлен, чтобы образовалосьтождество: (6x2 − 4xy − y2) − (*) = 4x2 + y2. Докажите, что значение выражения (13n + 29) − (4n − 7) кратно 9 при любом натуральном значении n. Известно, что 2a2b3 = −3. Найдите значение выражения: 1) 6a2b3; 2) 2a4b6. Вариант 4 Найдите значение выражения 72 - 0,4 ⋅ 53 . Представьте в виде степени выражение: 1) a5⋅a8; 2) a8 : a5; 3) (a5) 8; 4) 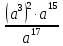 . . Преобразуйте выражение в одночлен стандартного вида: 1) −2a7b ⋅ (−3) ⋅a4b9; 2) (−3a3b2) 4. Представьте в виде многочлена стандартного вида выражение: (7b2 − 4b + 2) − (5b2 − 3b + 7). Вычислите: 1) 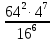 ; 2) ; 2) 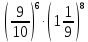 . .Упростите выражение: 216mn4 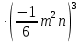 . .Вместо звёздочки запишите такой многочлен, чтобы образовалось тождество: (2x2 − xy− 2y2) − (*) = 4x2 − xy. Докажите, что значение выражения (15n − 2) − (7n − 26) кратно 8 при любом натуральном значении n. Известно, что 5x2y3 = −7. Найдите значение выражения: 1) −10x2y3; 2) 5x4y6. |
