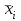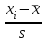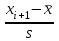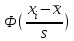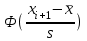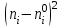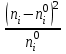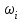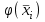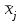Задача. Контрольная работа 2
 Скачать 151.78 Kb. Скачать 151.78 Kb.
|
|
ВАРИАНТ 10 Контрольная работа № 2 По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование строительных организаций региона по объему выполненных работ (млн. руб.). Результаты представлены в таблице:
Найти: а) границы, в которых с вероятностью 0,9973 заключен средний объем выполненных работ всех строительных организации региона; б) вероятность того, что доля всех строительных организаций, объем работ которых не менее 60 млн. руб., отличается от доли таких организаций в выборке не более, чем на 0,05 (по абсолютной величине); в) объем бесповторной выборки, при котором те же границы для среднего объема выполненных работ, (см. п. а)), можно гарантировать с вероятностью 0,9876. Решение: Так как дан интервальный ряд, то найдем интервальные полусредние – полусумма границ интервалов. 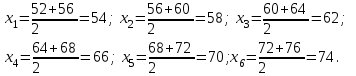 Определим выборочную среднюю: 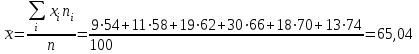 . .Определим выборочную дисперсию: 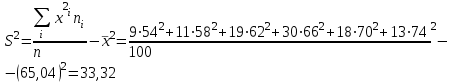 . .а) Для нахождения границ интервала, в которых с вероятностью 0,9973 заключен средний объем выполненных работ всех строительных организации региона, определим среднюю квадратичную ошибку выборки 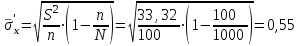 Предельная ошибка бесповторной выборки находится как 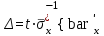 , , где t- аргумент функции Лапласа, соответствующий доверительной вероятности 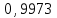 , т.е. определяет точность полученных результатов. Для заданной доверительной вероятности по таблице функции Лапласа находим, что значение ее аргумента будет равно t=3. , т.е. определяет точность полученных результатов. Для заданной доверительной вероятности по таблице функции Лапласа находим, что значение ее аргумента будет равно t=3. Следовательно, оценка генеральной средней (доверительный интервал) будет удовлетворять следующему двойному неравенству: 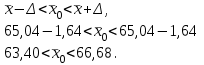 б) На основании вариационного ряда, определим количество всех строительных организаций, объем работ которых не менее 60 млн. руб.: 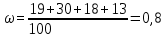 Средняя квадратическая ошибка собственно-случайной бесповторной выборки при оценке генеральной доли, находится по формуле: 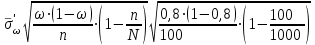 Вероятность того, что доля всех строительных организаций, объем работ которых не менее 60 млн. руб., отличается от доли таких организаций в выборке не более, чем на 0,05 (по абсолютной величине). определим по формуле: 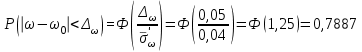 в) Для определения объема бесповторной выборки, при котором те же границы для среднего объема выполненных работ, (см. п. а)), можно гарантировать с вероятностью 0,9876, найдем значение аргумента функции Лапласа, при котором Ф(t)= 0,9876. По таблице найдем t=2,5. Объем повторной выборки 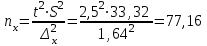 . .Тогда искомый объем бесповторной выборки: 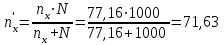 . .2. По данным задачи 1, используя 2-критерий Пирсона, на уровне значимости =0,05 проверить гипотезу о том, что случайная величина ξ – объем выполненных работ – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую. Решение: Для проверки гипотезу о том, что случайная ξ – объем выполненных работ – распределена по нормальному закону, используя 2-критерий Пирсона, необходимо найти критическое и наблюдаемое значение статистики. Для нахождения наблюдаемого значения статистики определим вероятность попадания случайной величины Х, распределенной по нормальному закону в каждый из интервалов [xi; xi+1] данного вариационного ряда по формуле: 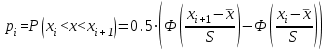 При этом предположим, что математическое ожидание нормального распределения совпадает с выборочной средней 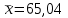 , а дисперсия - с выборочной дисперсией , а дисперсия - с выборочной дисперсией 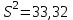 . . Результаты вычислений занесем в таблицу:
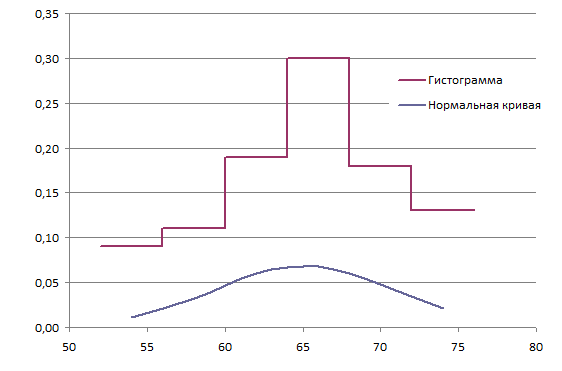
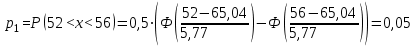 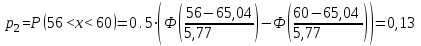 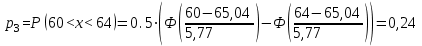 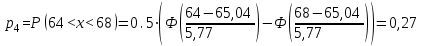 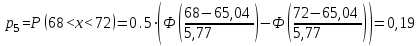 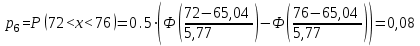 По найденным значениям вероятности определяем теоретические частоты по формуле: 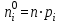 По найденным значениям частот и частотами, заданными в таблице определим наблюдаемое значение статистики 2: 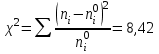 Критическое значение статистики определим по таблице в зависимости от уровня значимости α=0,05 и числа степеней свободы k=m-3=6-3=3: 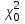 Поскольку полученное значение 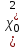 , то отвергаем гипотезу о нормальном распределении значения признака в вариационном ряде. , то отвергаем гипотезу о нормальном распределении значения признака в вариационном ряде. Построим гистограмму опытного распределения и соответствующую ей нормальную кривую. Для этого найдем частоты 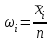 и плотность нормального распределения и плотность нормального распределения 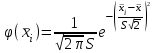 : :
 3. Распределение 100 средних фермерских хозяйств по числу наемных рабочих ξ (чел.) и их среднемесячной заработной плате на 1 человека η (тыс. руб.) представлено в таблице:
Необходимо: 1) Вычислить групповые средние 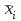 и и 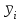 и построить эмпирические линии регрессии. и построить эмпирические линии регрессии.2) Предполагая, что между переменными ξ и η существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости =0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными ξ и η; в) используя соответствующее уравнение регрессии, оценить среднемесячную заработную плату одного рабочего в хозяйстве, в котором работают 10 наемных рабочих. Решение: Найдем серединные значения на интервалах xi и yi, для них найдем групповые средние по формулам 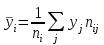 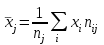 Результаты вычислений запишем в таблицу
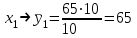 ; ;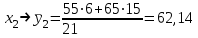 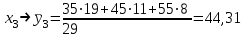 ; ; 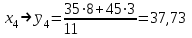 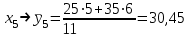 ; ;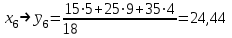 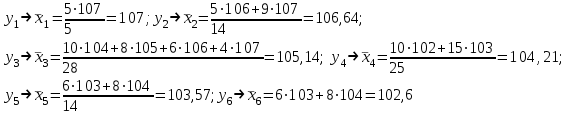 2. а) Найдем значения средних, входящих в уравнение регрессии: 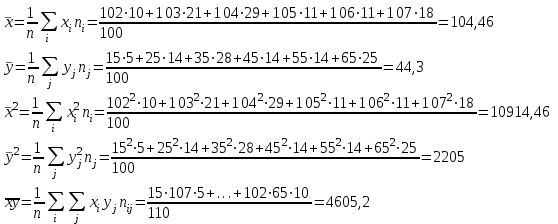 Найдем коэффициенты уравнения регрессии: 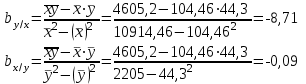 Уравнение прямой регрессии y на x 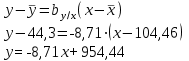 Уравнение прямой регрессии x на y 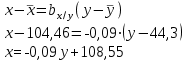 Построим графики уравнения прямых регрессий и эмпирические линии регрессии с помощью таблиц
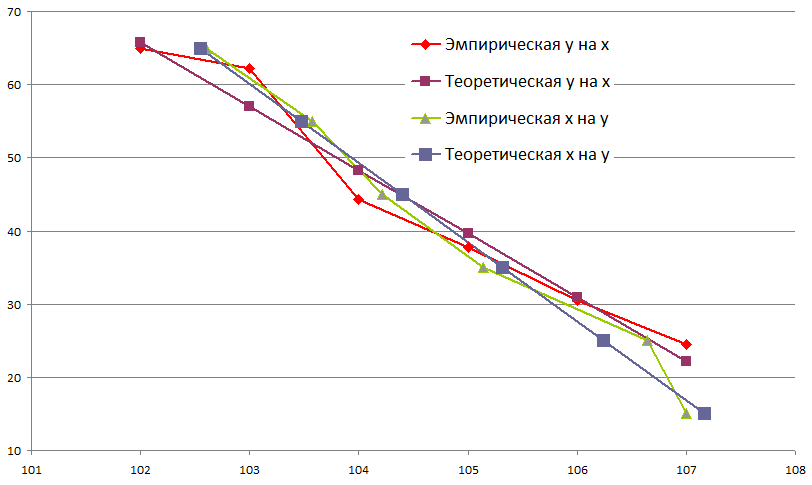 б) Для оценки тесноты и направление связи определим значение выборочного коэффициента корреляции r. Поскольку коэффициенты регрессии отрицательны, то 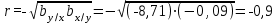 Поскольку коэффициент корреляции отрицательный, то наблюдается обратная связь. Так как коэффициент корреляции по абсолютной величине удовлетворяет соотношению 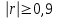 , то связь между ξ и η считается высокой. , то связь между ξ и η считается высокой.Для оценки достоверности коэффициента корреляции найдем значение критерия Стьюдента: 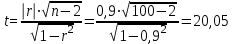 Найденное значение t – критерия значительно больше табличного 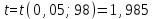 , поэтому принимается гипотеза о достоверности коэффициента корреляции на уровне =0,05 и о наличии тесной корреляционной связи между числом наемных рабочих ξ (чел.) и их среднемесячной заработной плате на 1 человека η (тыс. руб.). , поэтому принимается гипотеза о достоверности коэффициента корреляции на уровне =0,05 и о наличии тесной корреляционной связи между числом наемных рабочих ξ (чел.) и их среднемесячной заработной плате на 1 человека η (тыс. руб.).в) Поскольку среднемесячная заработная плата одного рабочего в хозяйстве характеризуется величиной η, то он может быть найден из уравнения прямой регрессии η на ξ при ξ =10. 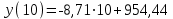 Среднемесячная заработная плата одного рабочего в хозяйстве, в котором работают 10 наемных рабочих, составляет 867,31 тыс. руб |