Математический анализ КР. Контрольная работа 2 вариант 4 По дисциплине Математический анализ

• Название: Контрольная работа 2 вариант 4 По дисциплине Математический анализ
• Анкор: Математический анализ КР
• Дата: 26.12.2021
• Размер: 298.5 Kb.
• Имя файла: Математический анализ КР.doc
• Тип: Контрольная работа; #318265

Министерство образования и науки Российской Федерации

ФГБОУ ВО «Кемеровский технологический институт пищевой промышленности (университет)»

Представительство г. Новокузнецк
Контрольная работа № ___2_________вариант № __ 4____

По дисциплине: _ Математический анализ_______________

Оценка работы _____________ Дата проверки _____________

Подпись преподавателя _________________________________

Дата поступления работы в институт _______________________

Номер по журналу регистрации __________________________

КОНТРОЛЬНАЯ РАБОТА №2

Вариант – 4
Задание № 1. Задана линия своим уравнением в полярной системе координат.

Требуется: 1) определить точки, лежащие на линии, придавая j значения через промежуток, равный p/8, начиная от j = 0 и до j = 2p; 2) построить линию, плавно, соединив полученные точки; 3) записать уравнение этой линии в декартовой системе координат.



Решение:

1) построим по точкам график функции .

к			к
0	0	2,00	9	202,5	4,17
1	22,5	-16,13	10	225	3,22
2	45	2,80	11	247,5	-31,08
3	67,5	5,36	12	270	2,02
4	90	15,25	13	292,5	-11,96
5	112,5	2,23	14	315	2,50
6	135	-10,12	15	337,5	7,45
7	157,5	2,11	16	360	8,70
8	180	48,87

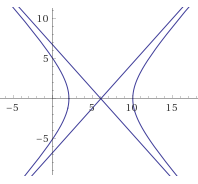Рис. 1
Найдем уравнение кривой в прямоугольной системе координат, начало которой совпадает с полюсом, а положительная полуось Ох с полярной осью.

Выразим прямоугольные координаты через полярные координаты по формулам:

;

тогда ; ; ; .

Следовательно, ; .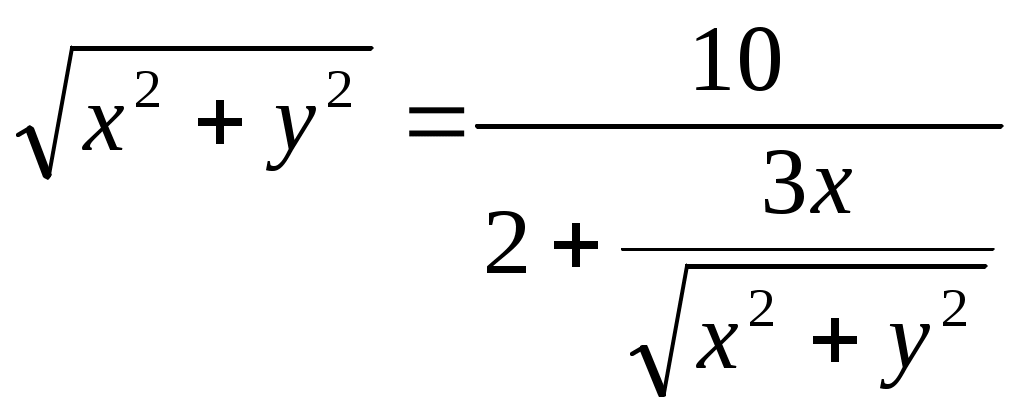

2) Определим вид кривой

; ; ;

- уравнение гиперболы с центром в точке О₁(6;0).
Задание№2. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.

а);

Решение:

Непосредственная подстановка предельного значения аргумента приводит к неопределенному выражению 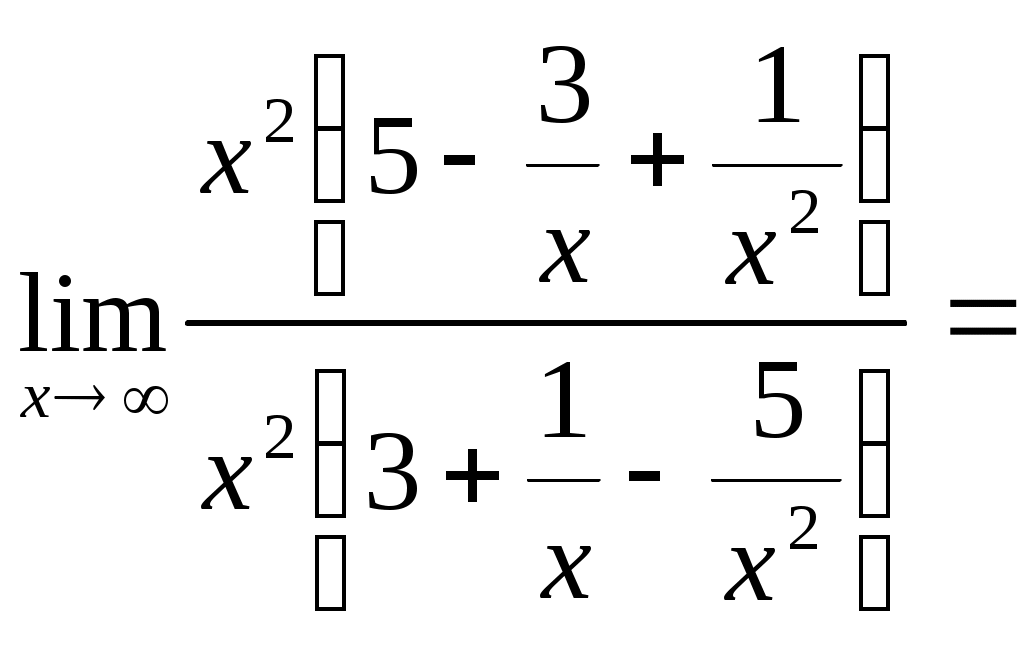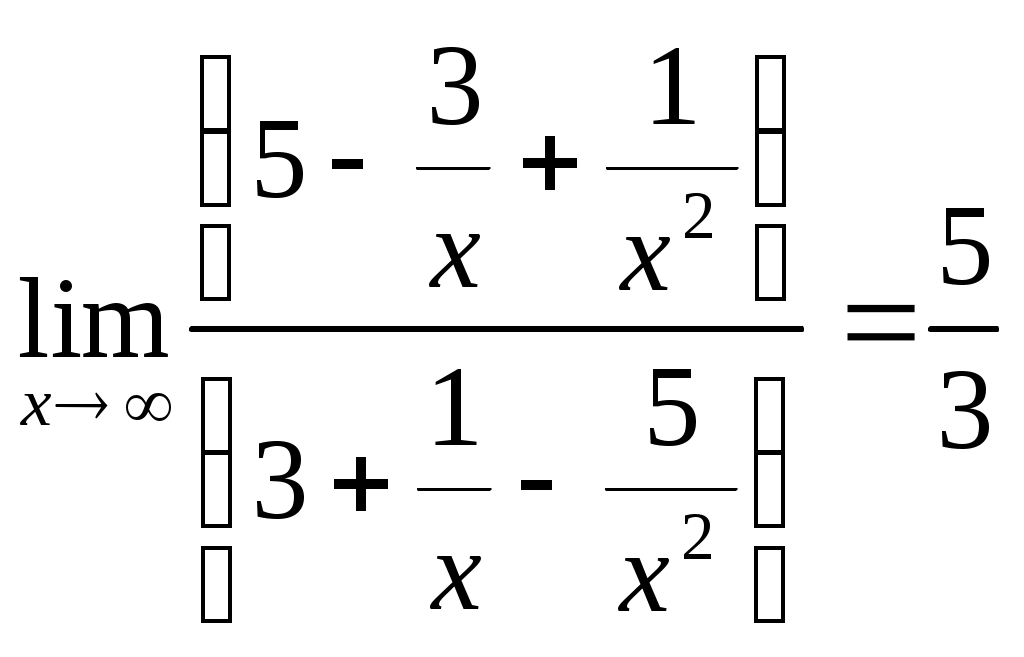. Чтобы раскрыть неопределенность вида , необходимо предварительно числитель и знаменатель дроби разделить на и применить основные теоремы о пределах и свойствах бесконечно малых величин:

.

Ответ: .
б) .

Решение:

Непосредственная подстановка предельного значения аргумента приводит к неопределенному выражению вида . Чтобы раскрыть неопределенность вида , необходимо числитель и знаменатель разложить на множители:

.

Ответ: .
в) .

Решение:

Непосредственная подстановка предельного значения аргумента приводит к неопределенному выражению вида . Чтобы раскрыть неопределенность вида , необходимо помножить числитель и знаменатель функции на выражение, сопряженное числителю и знаменателю .

.

Ответ:

г) .

Решение:

.

Преобразуем выражение



Пусть , тогда , при ,

Применим второй замечательный предел:

= = .

.

Ответ:


Задание №3. Найти производные первого порядка данной функции, используя правила вычисления производных.
1) .

Решение:

.
2) .

Решение: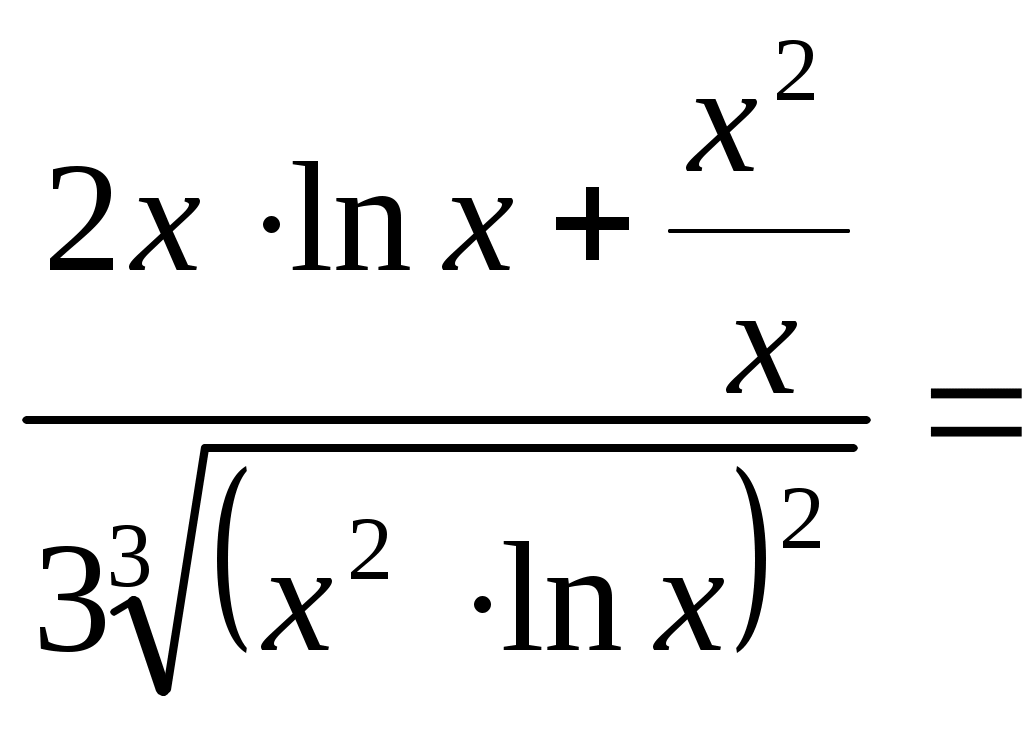

.
3) .

Решение: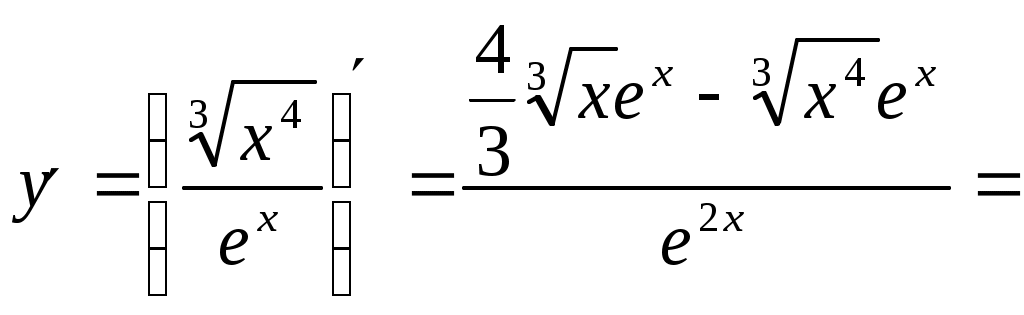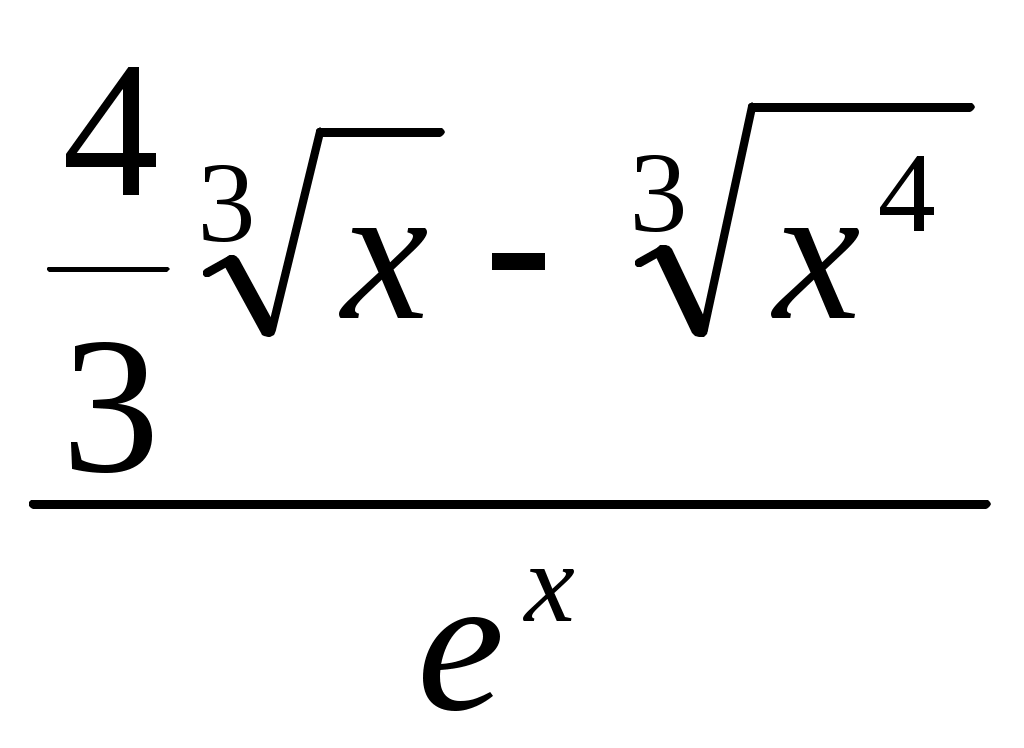

.
4)

Решение:

Применим формулу дифференцирования параметрически заданных функций:



;

;

.
Задание 4. Найти наибольшее и наименьшее значения функции на отрезке .

; .

Решение:

Находим критические точки данной функции:

.

при и .

Находим .

Вычислим значение функции на концах отрезка:

.

.

Итак, в точке , в точке .


Задание №5. Найти уравнение касательной и нормали к графику функции в указанной точке . Сделать чертеж.

, х₀= -2.
Решение:

Уравнение касательной к кривой: .

Уравнение нормали к кривой: .

;

.

.

Уравнение касательной к кривой: или .

Уравнение нормали к кривой: или .
Задание№6. Применяя дифференциальное исчисление, провести исследование функции и построить график.



Решение:

1. Функция не определена при . Область ее определения состоит из трех интервалов - ( ; ), ( ; ), ( ; ), а график из трех ветвей.

2. Если х=0, то у =2, график пересекает ось Оу в точке .

Если у=0, то , график пересекает ось Ох в точках и

3. Функция знакоположительна на интервалах ( ; -0,71), (-0,5;0,5) и (0,71; ); знакоотрицательна - (-0,71;-0,5) и (0,5; 0,71).

4. Функция является четной. График функции симметричен относительно оси Оу.

.

5. - вертикальные асимптоты: , ; ; .

Уравнение наклонной асимптоты будем искать в виде .

; .

у= 1 - горизонтальная асимптота.

6. Находим интервалы возрастания и убывания функции:

.

Функция возрастающая на интервале (0; 0,5) и (0,5; ); убывающая – ( ; -0,5) (0,5; 0).

7. (0; 2) – точка минимума.

8. Исследуем функцию на выпуклость:

;

Точек перегиба нет.

График выпуклый вниз на интервале (-0,5; 0,5); на интервале ( ; -0,5) и (0,5; ) - выпуклый вверх.

9. Изобразим график функции.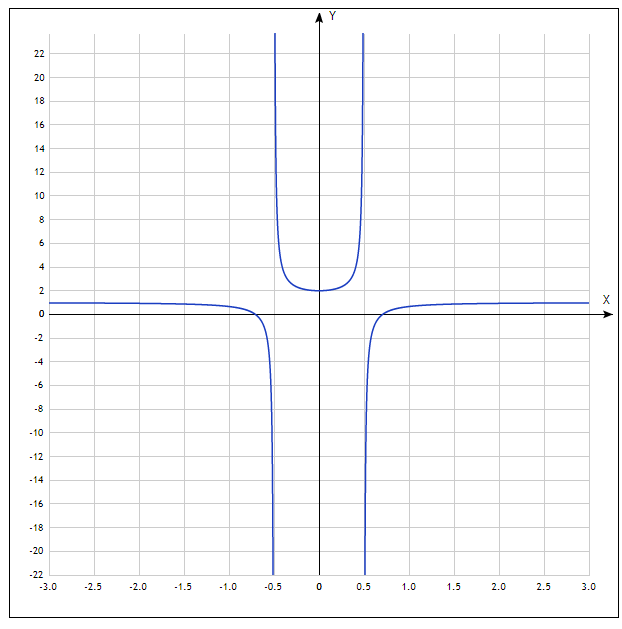