Главная страница
Навигация по странице:

  • КИРОВСКИЙ ФИЛИАЛ ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Контрольная работа №2 Вопросы к экзамену Для студентов специальности 1501

  • Таблица вариантов

    		•

    ТЕОРЕТИЧЕСКАЯ МЕХАНИКА ч2. Контрольная работа 2 Вопросы к экзамену Для студентов специальности 1501 " Автомобиле и тракторостроение"


    Скачать 429.5 Kb.
    НазваниеКонтрольная работа 2 Вопросы к экзамену Для студентов специальности 1501 " Автомобиле и тракторостроение"
    АнкорТЕОРЕТИЧЕСКАЯ МЕХАНИКА ч2.doc
    Дата14.10.2017
    Размер429.5 Kb.
    Формат файлаdoc
    Имя файлаТЕОРЕТИЧЕСКАЯ МЕХАНИКА ч2.doc
    ТипКонтрольная работа
    #9389


    Государственное образовательное учреждение

    высшего профессионального образования

    МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ

    КИРОВСКИЙ ФИЛИАЛ

    ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
    Контрольная работа №2
    Вопросы к экзамену

    Для студентов специальности 1501

    “Автомобиле- и тракторостроение”


    Составитель: Бакулин В.Н.

    г. Киров

    2003 г.
    ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

    Вопросы к экзамену


    1. Задачи статики и основные ее понятия. Аксиомы статики. Связи и реакции связей. Примеры связей. Сходящиеся силы. Сложение сходящихся сил. Разложение силы. Проекция силы на ось. Условия равновесия системы сходящихся сил.

    2. Параллельные силы. Сложение двух и многих параллельных сил. Центр Системы параллельных сил. Центр тяжести твердого тела. Определение центра тяжести однородных тел и фигур простой и сложной формы.

    3. Пара сил. Момент пары как вектор. Эквивалентные пары. Сложение пар, лежащих в параллельных и непараллельных плоскостях. Условия равновесия системы пар.

    4. Плоская система сил. Момент силы относительно точки. Теорема о параллельном переносе силы. Главный вектор и главный момент. Приведение плоской системы сил к одной паре. Условия равновесия плоской системы сил.

    5. Момент силы относительно оси. Зависимость между моментами силы относительно точки и относительно оси, проходящей через эту точку. Моменты силы относительно координатных осей. Приведение плоской и произвольной системы сил к данному центру. Главный вектор и главный момент. Зависимость главного момента от выбора центра приведения. Равнодействующая произвольной системы сил. Приведение системы сил к одной паре. Условия равновесия системы сил в общем случае. Инварианты системы сил.

    6. Трение. Виды трения. Коэффициент трения. Условия равновесия твердого тела при наличии сил трения.

    7. Задачи кинематики. Кинематическое определение механического движения. Принятые системы отсчета. Кинематика точки. Кинематические способы задания движения материальной точки (естественный, векторный, координатный). Прямолинейное движение точки. Уравнение движения точки. Равномерное и неравномерное движение. Скорость и ускорение точки в прямолинейном движении.

    8. Криволинейное движение точки. Уравнение движения точки. Скорость и ускорение точки в криволинейном движении. Определение модулей и направлений скорости и ускорения точки по их проекциям на оси декартовых координат и на естественные оси. Касательное и нормальное ускорение точки.

    9. Понятие о твердом теле и степенях его свободы. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях твердого тела при его поступательном движении.

    10. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение вращательного движения. Угловая скорость и угловое ускорение тела как скалярные и векторные величины. Линейные скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси. Выражение линейной скорости, касательного и нормального ускорения в виде векторных произведений.

    11. Сложное движение точки. Абсолютное, относительное и переносное движение точки. Скорость и ускорение точки в сложном движении. Случай поступательного переносного движения.

    12. Плоскопараллельное движение твердого тела. Уравнение плоскопараллельного движения. Разложение движения плоской фигуры на поступательное (переносное) и вращательное (относительное). Скорости точек плоской фигуры. Мгновенный центр скоростей. План скоростей. Понятие о подвижной и неподвижной центроидах. Ускорения точек плоской фигуры. Мгновенный центр ускорений и способы его определения.

    13. Динамика точки. Основные законы динамики. Инерциальная система отсчета. Две основные задачи динамики точки. Дифференциальные уравнения движения точки. Интегрирование дифференциальных уравнений движения материальной точки для простейших случаев. Начальные условия и определение постоянных интегрирования.

    14. Гармоническое колебание материальной точки под действием силы, пропорциональной расстоянию. Затухающие колебания с учетом закона сопротивления среды. Вынужденные колебания точки при наличии гармонической возмущающей среды без учета сопротивлений. Случай резонанса. Влияние сопротивления на вынужденные колебания. Максимальное значение амплитуды колебаний.

    15. Переносная и кориолисова сила инерции. Принцип относительности классической механики. Инвариантность уравнений динамики при переходе от одной системы к другой. Случай относительного покоя.

    16. Теорема о количестве движения материальной точки и механической системы. Теорема импульсов. Теорема о движении центра масс системы. Момент количества движения материальной точки относительно центра и оси. Теорема об изменении момента количества движения материальной точки. Случай центральной силы. Главный момент количества движения или кинетический момент механической системы относительно центра и оси. Теорема о кинетическом моменте системы.

    17. Элементарная работа силы и работа на конечном перемещении. Работа силы тяжести и системы сил, их аналитическое выражение. Теоремы об изменении кинетической энергии материальной точки и механической системы.

    18. Движение системы в потенциальном силовом поле. Понятие о силовой функции. Потенциальная энергия механической системы. Закон сохранения механической энергии.

    19. Динамика твердого тела. Моменты инерции системы и твердого тела относительно плоскости, оси и полюса. Центробежные моменты инерции. Эллипсоид инерции. Главные оси инерции. Физический маятник. Понятие о гироскопе. Элементарная теория гироскопических: явлений. Применение гироскопа в технике.

    20. Метод обобщенных координат системы. Обобщенные силы и способы их вычисления. Условия равновесия системы в обобщенных координатах. Дифференциальные уравнения движения механической системы в обобщенных координатах или уравнения Лагранжа второго ряда. Общие принципы и уравнения механики.

    21. Элементы механики тела переменной массы. Уравнение Мещерского. Реактивная сила и реактивное движение. Задачи Циолковского. Элементы космонавтики.

    22. Основы теории удара. Явление удара. Действие ударной силы на материальную точку. Теорема об изменении количества движения механической системы при ударе. Прямой центральный удар тела о неподвижную поверхность. Упругий и неупругий удар. Коэффициент восстановления при ударе. Прямой центральный удар двух тел.


    Контрольная работа для студентов-заочников технологических специальностей включает шесть задач Определение варианта задания проводится в соответствии с последней цифрой шифра.
    Таблица вариантов

    Номер задачи в каждой Номер задачи в каждой


    Вариант контрольной работе вариант контрольной работе

    1 1 11 21 31 41 51 6 6 16 26 36 46 56

    2 2 12 22 32 42 52 7 7 17 27 37 47 57

    3 3 13 23 33 43 53 8 8 18 28 38 48 58

    4 4 14 24 34 44 54 9 9 19 29 39 49 59

    5 5 15 25 35 45 55 10 10 20 30 40 50 60


    литература


    1. БатьМ. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. т. I, II.

    2. Воронков И. М. Курс теоретической механики.

    3. Старжинский В. М. Теоретическая механика.

    4. Тарг А. С. Курс теоретической механики. 9-е и последующие издания.

    5. Яблонский А. А. Курс теоретической механики.



    ЗАДАЧИ


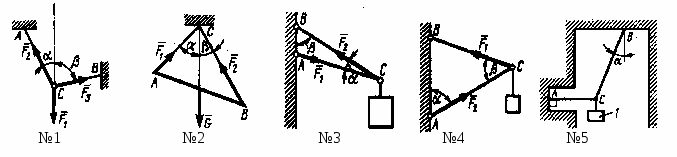
    1. Определить модуль силы F3 натяжения троса ВС, если известно, что натяжение троса АС равно F2 =15 Н. В положении равновесия углы =30° и  =75°. (7,76)

    2. Определить вес балки АВ, если известны силы натяжения веревок F1 =120 Н и F2 = 80 Н. Заданы углы  = 45° и  = 30° между вертикалью и веревками АС и ВС соответственно. (154)

    3. Груз удерживается в равновесии двумя стержнями АС и ВС, шарнирно соединенными в точках А, В и С. Стержень ВС растянут силой F2 = 45 Н, а стержень АС сжат силой F1 = 17 Н. Определить вес груза, если заданы углы  = 15° и  = 60°. (18,1)

    4. Шарнирный трехзвенник АВС удерживает в равновесии груз, подвешенный к шарнирному болту С Под действием груза стержень АС сжат силой F2 = 25 Н. Заданы углы  = 60° и  = 45°. Считая стержни АС и ВС невесомыми, определить усилие в стержне ВС. (48,3)

    5. Груз 1весом 2 Н удерживается в равновесии двумя веревками АС и ВС, расположенными в вертикальной плоскости. Определить натяжение веревки ВС, если угол  = 30°. (2,31)

    6. Два невесомых стержня АС и ВС соединены в точке С и шарнирно прикреплены к полу. К шарниру С подвешен груз 1. Определить реакцию стержня ВС, если усилие в стержне АС равно 43 Н, углы  = 60°,  = 30°. (24,2)

    7. Определить реакцию стержня АС, удерживающего в равновесии груз 1весом 14 Н с помощью цепи, намотанной на барабан Dи перекинутой через блок С, если угол  = 30°. (24,2)

    8. Груз 1весом 20 Н, подвешенный на канате, удерживается в равновесии двумя стержнями ОА и 0В, расположенными в вертикальной плоскости. Другой конец каната закреплен в точке С. Определить реакцию стержня ОА, если углы  = 40°,  = 45°. (21,7)

    9. Груз 1весом 10 Н подвешен с помощью каната, перекинутого через блок С и намотанного на барабан лебедки D. Определить усилие в стержне АС, если углы  = 45°,  = 60°. (26,4)

    10. Шар 1 весом 16 Н и шар 2 связаны нитью, перекинутой через блок D и удерживаются в равновесии. Определить вес шара 2,если угол  = 30°. (9,24)





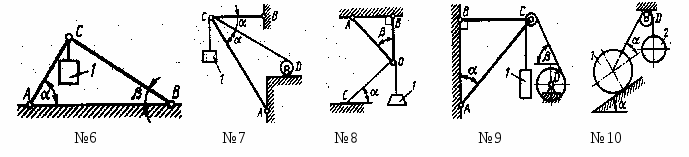
    1. Груз 1весом 60 Н удерживается в равновесии стержнями АС, ВС и DС, шарнирyо соединенными в точке С, и веревкой, переброшенной через блок Е под углом  = 30°. Определить усилие в стержне DС, если угол  = 45°. (73,5)

    2. Три стержня АС, ВС и DС соединены шарнирно в точке С. Определить усилие в стержне DС, если заданы сила F =50 Н и угол  = 60°. Сила Fнаходится в плоскости Оуz. (86,6)

    3. Три стержня АD, ВDи СDсоединены в шарнире D. Определить усилие в стержне СD, если груз 1имеет вес 20 Н, угол  = 45°. (28,3)

    4. Три стержня АD, ВD и СD соединены в точке D шарнирно. Определить усилие в стержне СD, если сила F =8 Н находится в плоскости Оуzи угол  = 20°. (0)

    5. Для подъема тяжелых деталей применяется тренога АОСВ и лебедка D. Определить усилие в стержне АС, если вес поднимаемого груза 1равен 60 Н, трос DСЕ лежит в плоскости Оуz, углы  = 60°,  = 45°. (19,1)

    6. Однородная плита весом G =100 Н удерживается в равновесии в плоскости 'чертежа тремя тросами АD, ВD и СD. Определить усилие в тросе СD, если угол  = 30°. Трос СD лежит в плоскости Оуz. (200)

    7. Три стержня АО, ВО и СО соединены в шарнире О. Определить реакцию стержня СО, возникающую под действием силы F =12Н, приложенной к шарниру О, если расстояния АВ=АО=АD. (13,9)

    8. Три стержня АО, ВО и СО шарнирно-стержневой конструкции соединены в точке О, к которой приложена сила F =18 Н. Определить усилие в стержне АО, если углы  = 30°,  = 45°. (25,5)

    9. Определить усилие в невесомом стержне СD, если дан вес груза G = 200 Н. Известны длины сторон шарнирно-стержневой конструкции СЕ= ВЕ= 2 м и АВ = ВD = 4 м. (127)

    10. Три стержня АD, ВD и СD соединены в точке D шарнирно. Определить усилие в стержне СD, если сила F =8 Н находится в плоскости Оуzи угол  = 45°. (0)







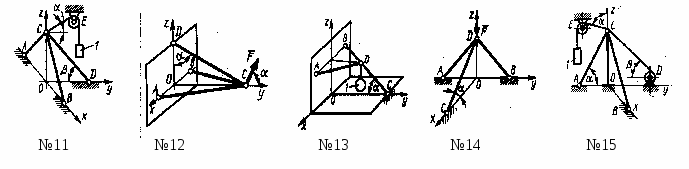
    1. Найти вертикальную составляющую реакции в шарнире С, если сила F =600 Н, размеры ВС=2АВ. (200)

    2. Найти вертикальную составляющую реакции в шарнире С, если к горизонтальному стержню АС приложена сила F1= 800 Н, к стержню СD - сила F2, угол  = 30°, размеры АВ=ВС. (200)

    3. Стержни АВС и СDсоединены между собой шарниром С. На стержень СDдействует пара сил с моментом M = 400 Н·м. Определить составляющую ХCреакции шарнира С, если длина СD = 2 м. (200)

    4. Два стержня соединены в шарнире В. Определить момент в заделке А, если силы F1 = 60 Н, F2= 50 Н. (240)

    5. Определить вертикальную составляющую реакции в шарнире А. (110)

    6. Определить вертикальную составляющую реакции в шарнире В, если сила F =850 Н, а размеры DС=СЕ=ВЕ. (401)

    7. Определить в кН·м момент М пары сил, при котором вертикальная составляющая реакции опоры А равна 10 кН, если размеры ВС= СЕ= 1 м. (25,8)

    8. Определить в кН силу F, при которой вертикальная составляющая реакции в шарнире А равна 9 кН, если размеры АВ=ВD = 1 м, СЕ= DЕ, момент пары сил М=6 кН·м. (4)

    9. Найти вертикальную составляющую реакции в шарнире С, если сила F =600 Н, размеры ВС=2АВ. (200)

    10. Н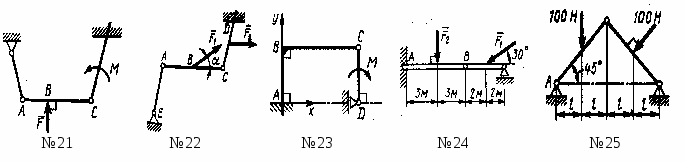
      айти вертикальную составляющую реакции в шарнире С, если к горизонтальному стержню АС приложена сила F1= 800 Н, к стержню СD - сила F2, угол  = 30°, размеры АВ=ВС. (200)





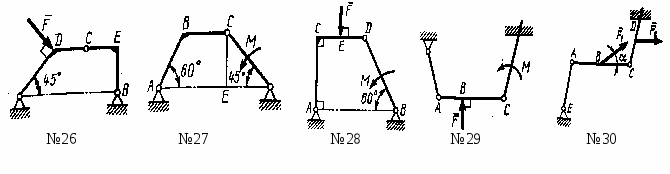
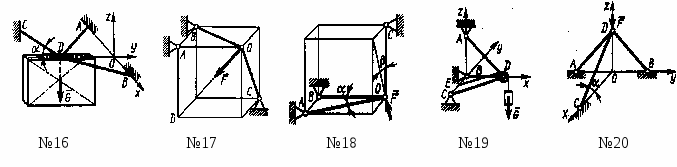
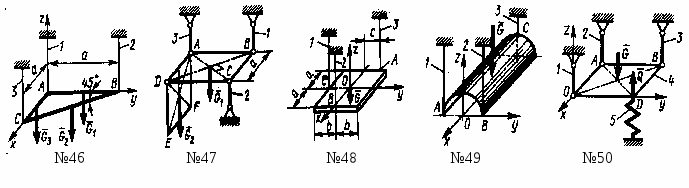
    1. Определить усилие в стержне 4. Сила F =340 Н. (481)

    2. Определить усилие в стержне 1. Сила F =380 Н. (806)

    3. Определить усилие в стержне 6. Силы F1= F2=380 H. (0)

    4. Определить усилие в стержне 8. Сила F =260 Н. (130)

    5. Определить усилие в стержне 5. Сила F =160 Н. Длины всех стержней одинаковы. (92,4)

    6. Определить усилие в стержне 6. Сила F =360 Н. (720)

    7. Определить усилие в стержне 5. Сила F =480 Н. (800)

    8. Определить усилие в стержне 3. Сила F =460 Н. (460)

    9. Определить усилие в стержне 3. Сила F =540 Н. (540)

    10. О
      пределить усилие в стержне 2. Силы F1= F2=520 Н. (735)





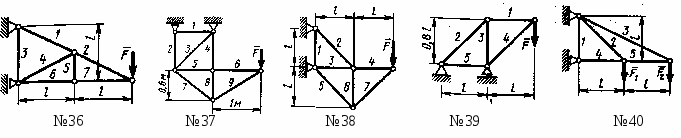
    1. На треноге АВ = ВС = АС покоится горизонтальная платформа с грузом G1=50 Н. Вес треноги иплатформы G2=500 Н. Векторы сил G1, G2и точка A находятся в одной вертикальной плоскости. Определить реакцию в точке А, если расстояния а=0,5 м, b =1 м и с= 1,5 м. (200)

    2. Горизонтальная однородная квадратная плита АВСDвесом G =500 Н подвешена в точках А, D, Е к трем вертикальным стержням 1, 2, 3. Определить усилие в стержне 1, если АD = 2АЕ. (500)

    3. Однородная квадратная плита АВСDзакреплена в горизонтальном положении с помощью трех вертикальных стержней 1, 2 и 3. Определить силу Q, которую следует приложить в точке А, чтобы стержень 3не испытывал нагрузку, если G =100 Н, а= 1 м. (100)

    4. Квадратная пластина АВСDвесом G =115 Н в горизонтальном положении закреплена шарнирно в трех вертикальных стержнях 1, 2 и 3. В точке А приложена вертикальная сила Q =185 Н. Из уравнения равновесия моментов сил относительно оси ВDопределить усилие в стержне 2. (185)

    5. Однородная пластина весом G =500 H в форме прямоугольного треугольника АВС вгоризонтальном положении висит на трех веревках, закрепленных в точках А, С и D. Определить натяжение веревки, привязанной в точке D если расстояние а=1 м. (250)

    6. Однородная треугольная сварная рама АВС в горизонтальном положении удерживается тремя вертикальными тросами 1, 2 и 3. Определить натяжение троса 3, если рамы вес частей рамы G1 = G2 = 101 Н, G2 = 143 H. (122)

    7. Пластинка АВСDзакреплена в горизонтальном положении с помощью шарниров и трех стержней 1, 2 и 3. Вес пластинки G1=10 Н. В точках А и Dк пластинке шарнирно подвешена вторая пластинка шириной EF = АDи весом G2 = 8 Н. Определить усилие в стержне 1, если расстояние а = 0,4 м. (4)

    8. Прямоугольная, однородная пластинка закреплена горизонтально с помощью трёх нитей 1, 2 и 3,закрепленных в точках А, В и С. Определить расстояние с расположения точки А от оси симметрии, при котором нити будут натянуты одинаково, если вес пластинки G = 3 Н, расстояния а = 0,2 м и b = 0,1 м. (0,1)

    9. Однородная оболочка весом G =40 кН в виде полуцилиндра радиуса Rвисит на трех вертикальных тросах 1, 2 и 3,закрепленных в точках А, В и С. Определить в кН реакцию в тросе 1, если известно, что реакция в тросе 3равна 20 кН. (10)

    10. На трех вертикальных стержнях 1, 2 и 3шарнирно закреплена горизонтальная прямоугольная платформа 4с размерами ОА = 1,5 АВ и весом G =1 кН. В точке D на платформу давит пружина 5 с силой Q =0,5 кН. Определить в кН реакцию в стержне 2. (0,5)








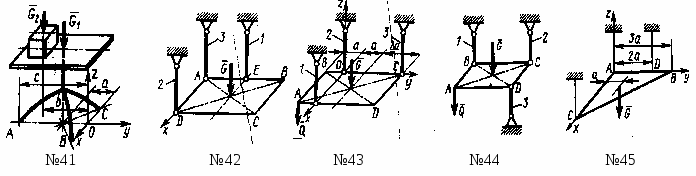
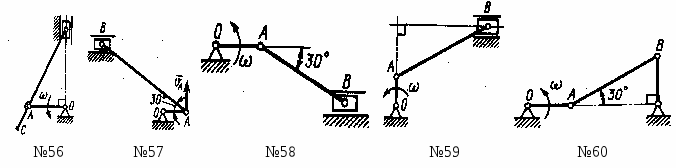
    1. Для данного положения механизма определить скорость точки С - середины шатуна АВ, если угловая скорость  = 1 рад/с; длины звеньев ОА=0,3 м; АВ=0,5 м. (0,3)

    2. Частота вращения коленчатого вала двигателя 4200 об/мин. Определить скорость движения поршня В, если в данный момент времени мгновенный центр скоростей Р шатуна АВ находится на расстояниях АР=0,18 м, ВР=0,10 м; длина кривошипа ОА=0,04 м. (9,77)

    3. Кривошип ОА длиной 0,5  и шатун АВ длиной 1,57  в данный момент времени находятся на одной прямой. Определить угловую скорость шатуна, если кривошип вращается с угловой скоростью  = 120120)

    4. Определить угловую. скорость кривошипа ОА кривошипно-ползунного механизма в указанном положении, если скорость точки О шатуна vD = 1 м/с, длина кривошипа ОА=0,1м. (10)

    5. Определить угловую скорость шатуна АВ кривошипно-ползунного механизма в указанном положении, если точка А имеет скорость vA = 3 м/с. Длина шатуна АВ = 1 м. (1,73)

    6. Определить угловую скорость кривошипа ОА в указанном положении, если скорость точки С шатуна vC = 4 м/с, длина кривошипа ОА= 0,2 м. (20)

    7. Определить угловую скорость шатуна АВ кривошипно-ползунного механизма в указанном положении, если точка А имеет скорость vA = 3 м/с, а длина шатуна АВ=1 м. (3,46)

    8. Определить угловую скорость шатуна АВ кривошипно-ползунного механизма в указанном положении, если точка А имеет скорость vA = 3 м/с, а длина шатуна АВ=3 м. (1,15)

    9. Определить угловую скорость кривошипа ОА в указанном положении, если скорость ползуна vB = 2 м/с, а длина кривошипа ОА=0,1 м. (20)

    10. Определить для показанного на рисунке положения шарнирного четырехзвенника угловую скорость звена АВ, длина которого 0,2 м, если точка A имеет скорость 1 м/с. (5,77)

    написать администратору сайта