Контрольная по высшейматематике. Готово. Контрольная работа 2 Задание 1 к разделу 1 а выполнить действия б найти корни уравнения
 Скачать 113 Kb.
|
|
Контрольная работа № 2 Задание 1 к разделу 1 а) выполнить действия: 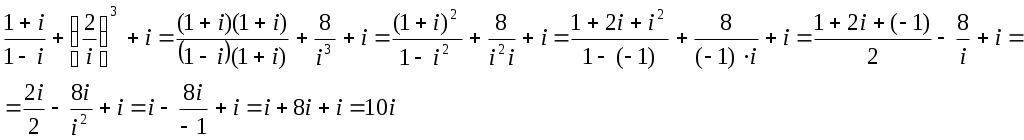  б) найти корни уравнения:    . В данном примере  , а значит, уравнение имеет ровно три корня.Модуль числа 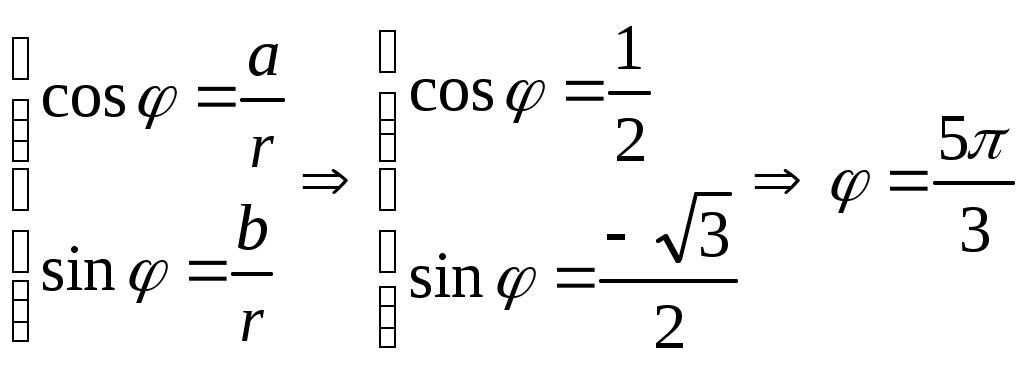 . Тогда 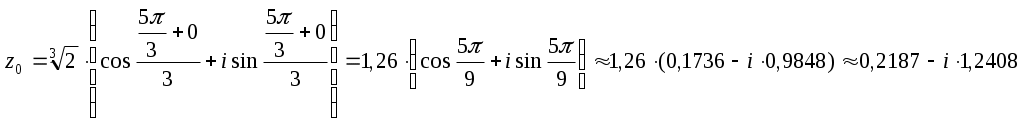 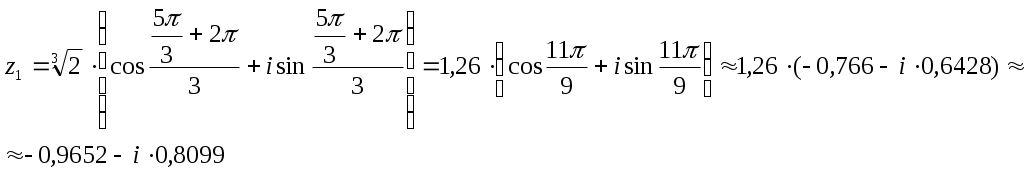 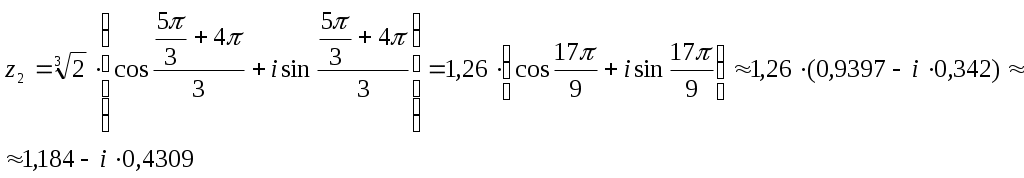 Задание 1 к разделу 2 Найти пределы функций, не пользуясь правилом Лопиталя: а)  При подстановке предельного значения получаем неопределенность 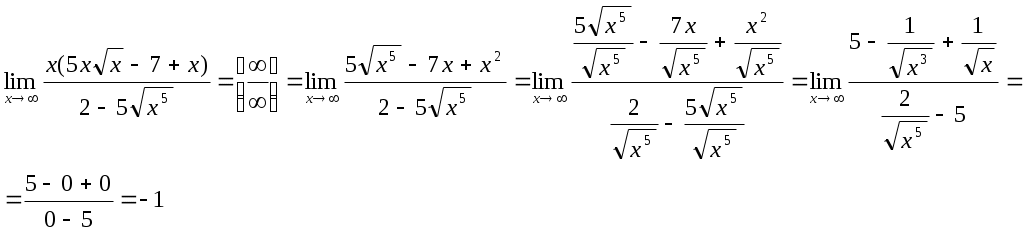 , чтобы избавиться от этой неопределенности, числитель и знаменатель почленно разделим на наивысшую степень x, в нашем случае  , затем снова подставим предельное значение x. б)  Подставка предельного значения аргумента x=1 приводит к неопределенному выражению  Для устранения этой неопределенности разложим числитель на множители и сократим дробь. Решение запишем следующим образам: 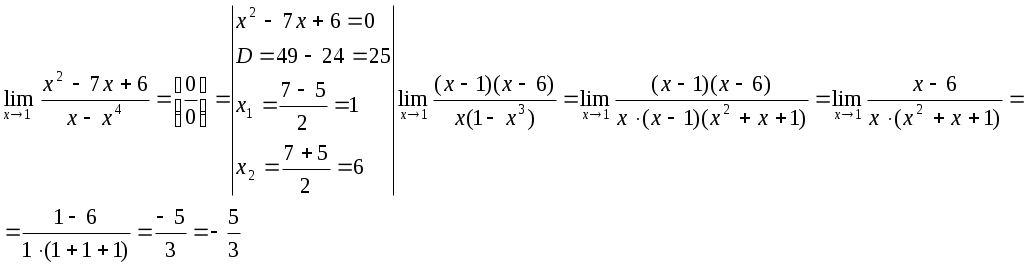 в) 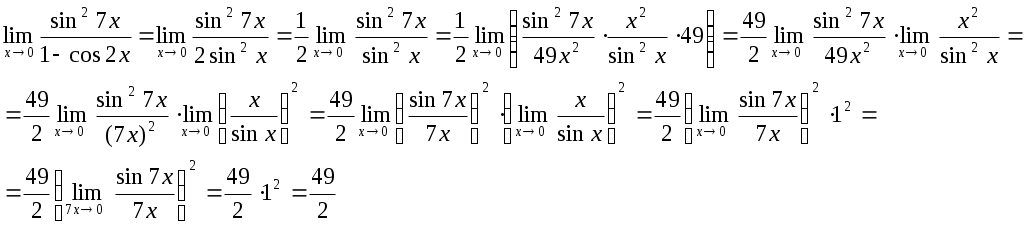  Использован I замечательный предел. г) 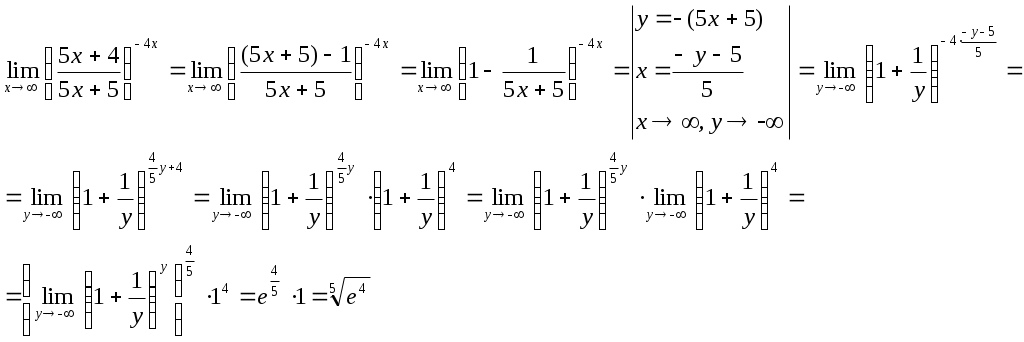  Использован II замечательный предел. Задание 1 к разделу 3. Задана функция  и два значения аргумента x1=5 и x2=9. Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, и сделать схематический чертеж.Решение. Функция определена при всех значениях х, кроме х=9. Найдем односторонние пределы:   В точке х=5, функция непрерывна.   В точке х=9, функция имеет разрыв II рода. 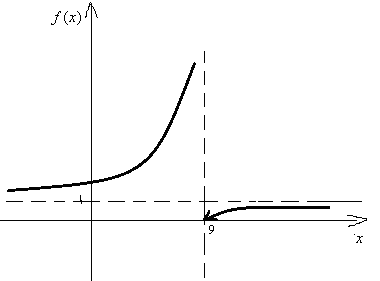 Задание 2 к разделу 3. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж. 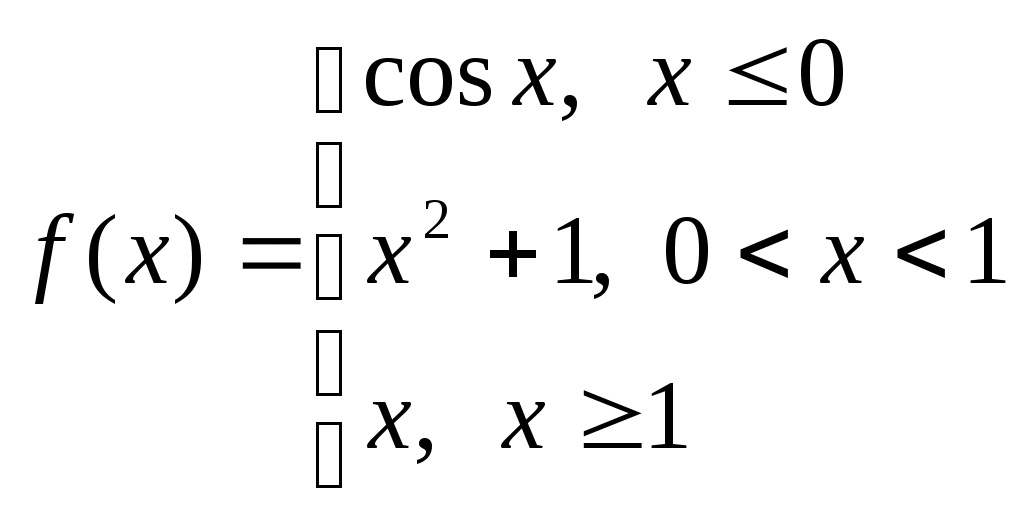 Решение. Числовая ось разбита на три интервала:  .Исследуем функцию на непрерывность в точках: х=0, х=1. Найдем односторонние пределы:   В точке х=0, функция непрерывна.   В точке х=1, функция имеет разрыв I рода. 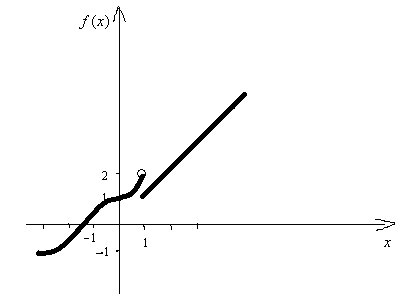 |